立足认知结构 探究变式策略
■李琳琳
对于数学变式问题的分类,有许多不同的分法,笔者这里倾向于常州市特级教师潘建明老师的界定,将变式分为概念变式和过程变式,过程变式又分为水平变式和垂直变式。变式既是一种重要的思想方法,又是一种重要的教学策略,在教学过程中要合理运用不同的变式策略,立足学生的认知结构,逐步推进,层层深入。
一、巧用概念变式,促进知识内化
初中数学中有大量的概念,它是数学知识的重要组成部分,也是导出数学定理和法则的逻辑基础。学生对数学概念的掌握会受许多因素的影响,其中的变式至关重要。概念变式不变的是概念的本质属性,变的是概念的非本质属性。概念变式的目的是为了让学生经历概念形成过程,即概括、抽象、具体化,从而使学生获得的概念更加准确、更加深刻。这里的概念变式我们分为标准概念变式(即概念外延的变化)和非概念变式(即举反例)。
[案例1]在学习苏科版八年级下册“11.1反比例函数”时,笔者给出了三个实际问题情境,用函数关系式表示下列情境中两个变量之间的关系:
(1)小明家距离学校5000m,他到校的时间y(h)随骑车速度x(m/h)的变化而变化;
(2)已知菱形的面积为24cm2,一条对角线长n(cm)随另一条对角线长m(cm)的变化而变化;
(3)实数a与b的积为-10,a随b的变化而变化。
师:很好,请同学们观察这三个式子有什么共同特征?你能用一个一般的式子表达出来吗?
生2:都有两个变量。
生3:都是函数。
生4:函数的右边都是一个分式。
生6:k≠0,自变量x≠0。
师:你能否对这种函数下个定义呢?
师:请判断哪些是反比例函数?

学生开始辨析反比例函数的形式,师生共同总结反比例函数的另外两种形式。
此案例属于标准概念变式,这里通过三个实际背景的问题情境,变换反比例函数的非本质属性,引导学生抽象出反比例函数的本质属性。在概念的教学中我们既要注重对概念的传授,也不能忽视概念的背景介绍,要让学生先抓住事物的本质属性,再给学生创造从多个侧面、多个角度去理解概念的机会。
[案例2]在学习苏科版七年级上册“6.3余角、补角、对顶角”时,对顶角的概念学生比较容易混淆。我们可以通过非概念变式来进行辨析,使学生轻松掌握对顶角的概念。
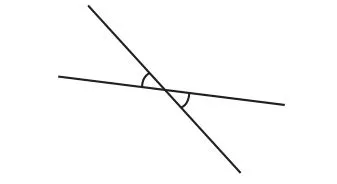
概念图像

非概念变式图像
在概念形成以后,应针对概念的内涵和外延设计辨析型题目,可以列举具有本质属性的事物或不具有该本质属性的事物的辨析,达到深化概念理解的目的。另外,概念变式的运用要掌握时机,如果在学生没有形成初步概念时就运用变式,将会干扰学生对概念的理解,所以我们要关注对概念变式教学的合理运用。
二、活用过程变式,联系知识结构
过程变式是指,学生通过概念、定理、命题等的学习过程,获得多层次的活动经验。在概念、定理、命题形成的过程中,过程变式反映了它们形成的历史过程和逻辑过程,在这样一个过程中,学生的新旧知识之间的联系得以建立,解题的经验和策略得以积累和提升。
过程变式中最具代表性的是水平变式和垂直变式。水平变式通常变更问题的背景,在同一思维水平上解决同一类问题。我们在教学中常用的策略有:(1)变换背景;(2)特殊到一般;(3)基本图形变式;(4)条件结论变式;(5)实际应用。垂直变式是思维逐步深入的过程,由表层学习转向结构学习,问题逐渐升华,进而加深对数学深层次价值和数学本质的体会。
[案例3]在学习苏科版九年级下册“6.4探索三角形相似的条件(2)”时,给出例题:
已知:如图1,∠A=∠E=∠BCD=90°,图中存在相似三角形吗?并说明理由。
变式1.已知:如图2,∠A=∠E=∠BCD=70°,图中存在相似三角形吗?并说明理由。
变式2.已知:如图3,∠A=∠E=∠BCD=130°,图中存在相似三角形吗?并说明理由。

图1
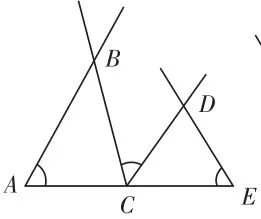
图2

图3
以上的源问题与两个变式问题中,给出的度数不同,图形也不同,但解决问题的方法是相同的,思维量是相当的,学生能感受到多题可以一解。实际上这是我们总结的相似问题中的“一线三等角”模型,水平变式有助于学生对数学模型的认识和解题策略的认识,改变学生孤立、静止地看待问题的思维习惯,帮助他们把握数学的内在规律,形成“以不变应万变”的能力。
数学教学中结构性变式的设计遵循认知的连续性,通常是从源问题到变式题,从水平变式到垂直变式,水平变式发展学生思维的广度,垂直变式发展学生思维的深度。但在教学中还要注意合理安排水平变式的“量”和垂直变式的“度”,才能达到既有量的积累,又有质的飞跃。

