环形放射状路网拓扑结构交通拥堵特性

朱远祺，屈云超*，刘浩，吴建军

(1.北京交通大学轨道交通控制与安全国家重点实验室，北京 100044；2.北京市交通信息中心，北京 100044)

随着城市经济快速发展、居民的出行需求与城市道路交通供给能力之间的矛盾日益加剧，交通拥堵已经成为现代城市的通病。为探究交通拥堵的产生机理，有学者针对交通出行需求进行了研究，陈团生[1]基于出行链、基于活动等方法，分析了通勤者的出行规律和出行特征。周涛等[2]对人类出行行为的时空特性进行了实证研究和建模，对交通出行行为的时空规律进行了总结。此外，特殊的道路网络结构也引起了部分学者的关注，例如我国的新疆特克斯县(又名“八卦城”)具有环形放射状路网结构，道路上虽然没有红绿灯但是交通仍有序运行。刘泉[3]从城市形态的角度出发，探究了八卦城这一独特路网结构的形成渊源。曹炜威[4]探究了环形放射状道路网络对偶图的小世界和无标度特性，发现其轴向主干道具有较高的度和中介中心度。

近年来，也有学者将交通需求与路网结构进行综合研究，Wu等[5]构建了规模相近、结构不同的复杂网络拓扑，通过UE(user equilibrium)结果的路段流量,定义了拥堵失效，并用拥堵边数的占比评价了3种典型路网拓扑的拥堵演化特点。Zhao等[6]研究了不同的度分布下几种复杂网络流量承载能力的差异，印证了无标度网络较为优良的分摊流量特性。此类研究存在两点不足：一是生成需求的方法过于简单，仅从网络节点中随机选取起讫点增加固定数量的OD，没有考虑需求的空间分布特性以及出行距离对交通需求量的影响；另一方面，此类研究的主体都是复杂网络，缺乏对平面拓扑结构的探讨。因此，本文对特定空间特性交通需求下的环形放射状路网结构的交通拥堵特性进行了深入研究。

本文从实际出租车GPS数据提取出了一种典型的出行直线距离分布，并设计了一种能满足出行直线距离分布的需求构造方法，用以生成符合真实空间特性的出行需求。然后，为对比研究不同的平面拓扑结构下的拥堵特性，构造了与特克斯县同等路网规模、路段总长、路段通行能力的环形放射状网络和方格网络。最后，采用静态交通配流得到UE平衡流量模式，并通过定义4种拥堵指标，评价了不同网络拓扑结构在不同需求和供给条件下的路段拥堵特性。结果显示，环形放射状网络具有优于方格网络的交通运行状态。

1 交通需求生成模型

研究表明，交通网络上的出行距离受空间阻力的影响，概率分布上呈现出随步长增加概率减小的趋势，其中负指数分布、幂律分布、对数正态分布是较为常见的概率分布函数[2]。

由于真实的城市道路交通需求难以获取，本文从国内多座城市的出租车GPS数据中提取个体用户每次出行的直线距离，分析了出行直线距离的统计分布特性，设计了一种满足该分布的交通需求生成方法，用于生成交通网络上的出行需求。

1.1 基于出租车GPS数据的OD直线距离分布

本文使用了北京、南京、上海、深圳、太原、天津、银川7座城市的GPS数据，根据“载客状态”字段提取出所有载客OD的起讫点GPS坐标，并利用Haversine公式计算了OD的平面直线距离。对各个城市的出租车OD直线距离进行频数统计，绘制了出行量占比与出行OD距离的关系如图1a所示。图中，σ、μ为对数正态分布的参数；R2为最小二乘法拟合的决定系数。

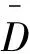
(1)

图1b表明，大部分城市的出租车载客直线距离分布按城市路网直径修正后趋于统一，说明出租车OD直线距离与城市路网的规模密切相关。其OD直线距离概率密度函数fd的峰值集中在2 km左右，平均出行距离集中在4～6 km，服从式(2)所示的对数正态分布。式(2)中，d代表OD的直线距离，μ和σ分别代表对数正态分布变量对数的平均值与标准差。

(2)

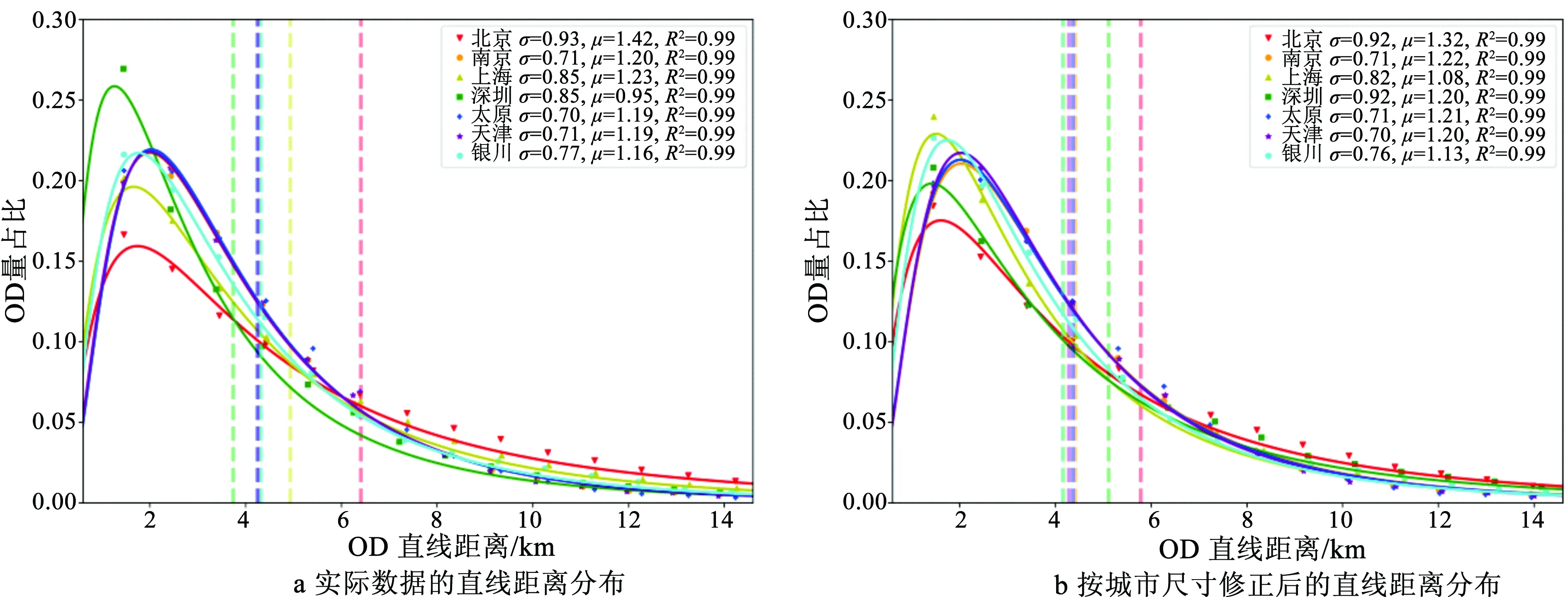
图1 国内多座城市出租车GPS数据提取的直线距离分布Fig.1 Euclidean distance distribution extracted from the taxi GPS data

1.2 基于对数正态分布的交通需求生成

由于路网的节点在平面区域的分布并不均匀，若直接对节点对进行初始OD生成，容易在高密度节点的区域生成过多的初始交通需求。为生成出行直线距离分布的概率密度函数为f(d)、OD总量为T的交通需求，本文设计了一种基于网格小区划分的需求生成方法。首先将路网的节点分为若干小区，然后以小区为基本单元按特定直线距离分布f(d)和总量T进行需求生成，最后将网格小区间的需求OD随机分配到节点对上，具体步骤如下：

(1)小区划分

若平面拓扑网络中包含m个节点{1,2,…，m}，划分为k个小区Z1，Z2，…，Zk，Zp的中心坐标记为(Xp,Yp)。

(2)小区间OD量生成

(3)节点间OD量生成

将Tpq随机分配至所有起点i∈Zp，终点j∈Zq的节点对(i,j)上，记作Tij，生成初始OD矩阵，需求生成完毕。

运用上述方法，采用式(2)的对数正态分布,分别绘制了OD总量(T)为10 000、30 000、50 000出行需求的直线距离分布，如图2所示。

图2 不同需求总量下的OD距离分布Fig.2 OD distance distribution under different demand

结果表明，不同需求总量下的OD距离分布形态均服从对数正态分布，上述需求生成方法有效。此外，分布峰值右偏说明采用实际出租车GPS数据拟合的出行距离分布在小规模路网上生成的需求以长距离出行为主。

由于采用上述方法生成的OD存在一定的随机性，这种随机性对网络平衡态的流量特性可能产生影响。本文将相同的T(30 000)采用相同的直线距离分布(μ=1.2,σ=0.8)配流至同一路网(2.1节中的特克斯)，重复进行了1000次随机需求生成、UE平衡配流及指标计算(具体方法见2.3节)，统计分析了拥堵相关指标的均值收敛速度和分布形态，如图3所示。图3a展示了指标均值(蓝色实线)随实验次数增多趋于稳定的过程，图3b展示了该指标的统计直方图分布形态，实验结果表明随机性导致的拥堵指标波动近似服从正态分布，且可通过多次重复实验取平均来减小需求随机性带来的影响，后续研究中的所有指标均采用200次实验的均值作为参考。

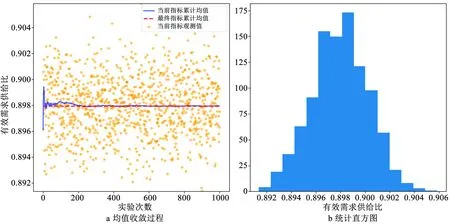
图3 有效需求供给比均值收敛过程和统计直方图Fig.3 Convergence and statistical histogram of the demand to supply ratio

2 典型路网结构的交通拥堵特性

2.1 典型路网构建

为研究环形放射状网络的拥堵特性，本文提取了特克斯实际路网，并构造了规则的环形放射状网络和方格网络进行对比研究，网络拓扑结构如图4所示。

图4 不同网络拓扑结构Fig.4 Topology of different road networks

首先，利用Python开源模块osmnx[7]获取了新疆特克斯县城区路网底层数据，利用Pyproj模块对GPS坐标进行了平面投影，构建了特克斯实际路网拓扑结构，如图4a所示，图中路段粗细代表车道数量,该网络具有4环16轴的环形放射状路网骨架，其中包括8条双向四车道的主干路(较粗)和8条双向双车道的次干路(较细)。

然后，构建了路网直径、路段总长、路段限速、路段通行能力均接近实际特克斯的环形放射状网络拓扑结构如图4b所示。环形放射状网络与实际特克斯的区别之处为前者所有路段的车道数为后者的均值，用以观察相同拓扑结构下，均匀的路段车道数对网络拥堵状态的影响。

此外，为对比研究环形放射状路网的拓扑结构，还设计了方形网格路网(图4c)，其路网直径、路段总长、路段限速、路段通行能力都与上述路网均为接近。3种网络的具体参数见表1。

表1 不同网络拓扑结构的各项参数

2.2 静态交通分配

交通系统中，路网上的流量受路径选择机制作用，逐渐向平衡态演化。交通分配就是将初始OD需求按照Wardrop用户最优原则分配到路网中的各个路段上，求出各条路段上的交通流量[5]。

Wardrop提出的平衡配流准则为：在起终点之间所有可供选择的路线中，使用者所利用的各条路线上的出行费用全都相等，而且不大于未被利用路线上的出行费用。该平衡状态在Beckmann模型中被表述为式(3)。

(3)

本文采用经典的Frank-Wolfe算法[8]对不同需求和路网拓扑结构下的交通网络进行静态平衡配流，得到路段流量模式，其中需求的生成采用了1.2节的方法。

2.3 拥堵特性分析

为描述网络上路段流量模式的拥堵特性，本文采用了4个基于路段流量和路段通行时间的指标[9]，如式(4)所示。

(4)

其中,xe为路段e的流量,Ce为路段e的通行能力,V/C的平均值可以体现路网整体的拥堵水平,V/C的极大值可以反映路网中最拥堵路段的拥堵水平。

(5)

其中,E为路网中所有的边,le为路段e的长度,Γ为有效需求供给比。该指标代表了非零流路段的路长加权的需求供给比例。

(6)

式(6)中,te为路段e的通行时间,t0为路段e的自由流时间,ε为额外拥堵时间占比。该指标可以从出行时间的角度评价路网拥堵程度。

图5为需求增量加载下的3种网络的拥堵状态指标计算结果。结果表明，环形放射状网络的4项指标均明显优于特克斯网络，说明统一的路段车道数能有效避免少数低通行能力路段带来的局部拥堵。此外，从有效需求供给比(图5c)和额外出行时间占比(图5d)看，环形放射状网络供给更好地满足了该OD直线距离分布下的交通需求，路网的总额外拥堵时间占比降低了接近25%。图5b中，特克斯和环形放射状网络的最拥堵路段V/C均大于方格网络。说明环形放射状网络的局部拥堵现象较严重。

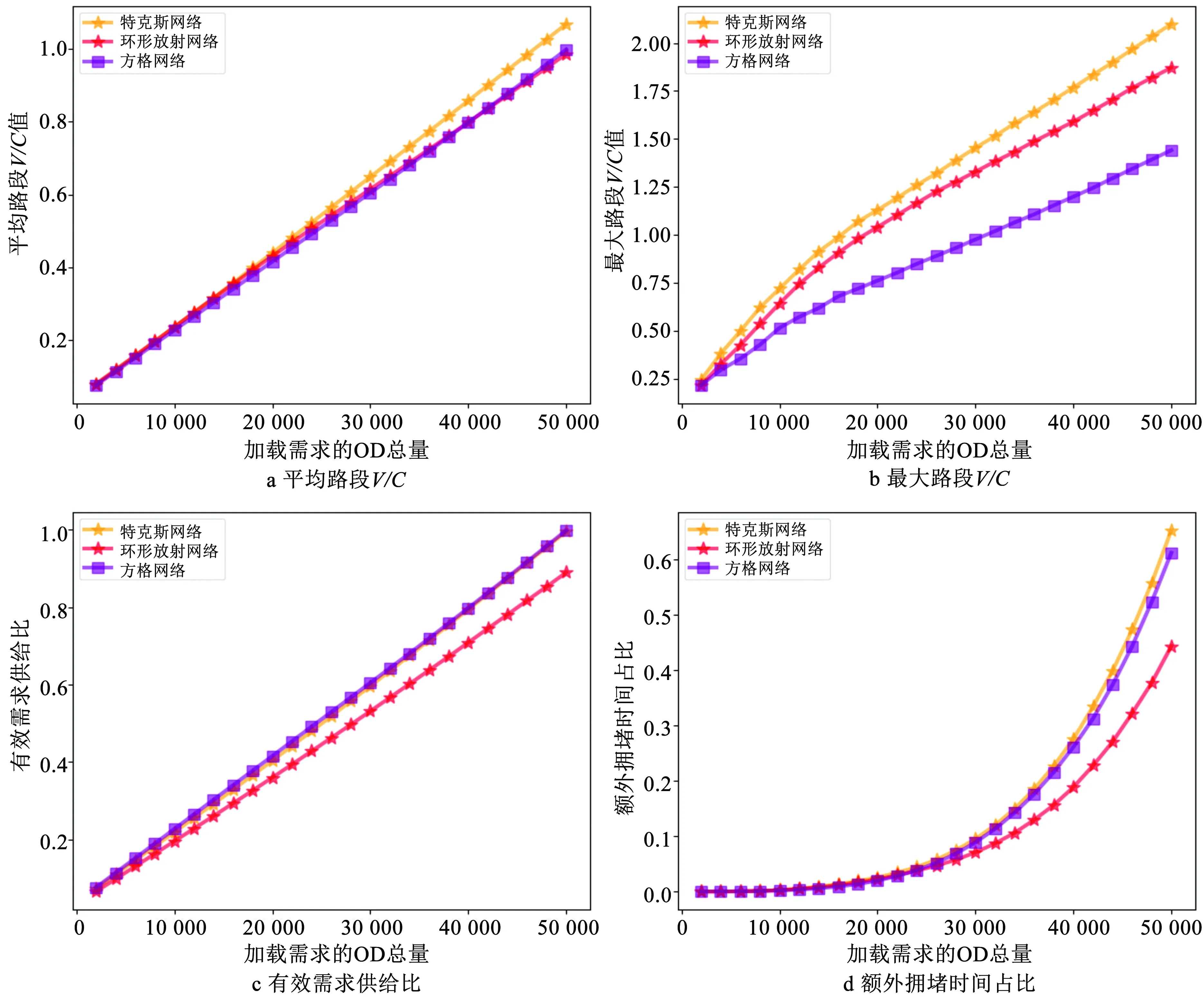
图5 增量OD需求下不同网络拥堵指标变化Fig.5 Changes in different network congestion indicators

为观察不同网络发生拥堵的具体区域，本文根据路段V/C的数值绘制了不同网络在T为20 000时的拥堵状况，如图6所示，图上路段颜色由浅至深分别代表路段V/C由低到高。可以发现，图6a、6b两种环形放射状网络的拥堵路段集中在网络中心区域，而图6c中方格网络的拥堵路段分布相对分散。原因之一是本文生成的初始OD需求以长距离出行为主，这种OD有更大概率穿过网络中心区域；另一方面，特克斯和环形放射状网络的中心区域路段较短，而UE假设下的用户路径选择机制导致较短路段更易吸引流量。两方面的原因造成了特克斯和环形放射状网络的中心区域过于拥堵。

图6 不同网络的路段拥堵情况(T=20 000)Fig.6 Congestion in different road networks (T=20 000)

3 结论

本文提出了一种基于出行距离分布的平面网络需求生成方法，并从实际数据中找到较具代表性的OD直线距离分布。用仿真实验结果验证了小规模环形放射状结构在该直线距离分布的需求下，确实具有优于方格网络结构的缓解拥堵的能力。环形放射状网络在特定直线距离分布下的OD增量加载过程中，大部分拥堵特性指标的表现均优于常见的方格网络，重要的原因是采用实际出租车数据提取的出行直线距离分布生成的交通需求，其直线距离分布的峰值接近2 km，而本文研究的路网规模较小，导致其上的出行需求有极大概率通过网络中心区域。环形放射状结构的路网具有内密外疏的供给分布特性，在长距离为主的OD需求下具有优于方形网格路网的分摊流量的特性。此外，实验结果中不均匀的车道数带来的不利影响和环形放射状路网中心区域的局部拥堵也为特殊结构的城市道路交通规划和管理提供了参考。

本研究的局限性同样需要引起注意，城市道路交通系统中，不同出行方式、来源的数据所代表的用户群体、出行时空特性各不相同。鉴于数据基础有限，本文在拟合出行直线距离分布时仅采用了出租车GPS数据，未能充分体现城市内部道路交通出行的多样性。若在后续研究有更多数据基础，可以通过融合多源数据预测交通出行需求时空分布特性，从交通供需匹配的角度对城市道路网络结构进行更深入的研究。