基于希尔伯特变换的光纤分布式声波测量技术
吕公河,刘雪洁,牟风明,刘小会
(1.中石化石油工程地球物理公司,北京 100020;2.中石化石油工程地球物理公司胜利分公司,山东 东营 257000;3. 齐鲁工业大学(山东省科学院),山东省科学院激光研究所,山东 济南 250103)
光纤分布式传感系统因其检测范围大、单位成本低廉、安装简便以及监测方式隐蔽等优点,已广泛应用于周界安防、建筑结构安全监测等领域[1-6]。其中,基于后向瑞利散射的相位敏感光时域反射技术(phase sensitive optical time-domain reflectometer,φ-OTDR)是现今最前沿的光纤分布式传感技术,国内外研究的重点在于提高监测距离、缩小空间分辨率以及如何全面获知需探测信息[7]。而在如何全面获知需探测信息方面,更强调进一步实现对外信号进行频率、相位、振幅和位置的实时解调,目前主要有两种方式:(1)强度解调。光路上直接将采集到的后向瑞利散射光强信号进行差分、平均、滤波等处理[8],其特点是系统光路简单,只需一个光电探测器(PD)直接采集,但仅能准确解调频率与位置,相位和振幅信息误差较大。(2)相位解调。光路上采用将后向瑞利散射光通入附加的迈克尔逊干涉仪,使用相位载波(PGC)、3×3耦合器法对相位进行解调[9-10],其特点是能准确解调频率、相位、振幅与位置信息,但系统光路结构复杂,干涉解调所需PD数量较多、成本较高。
基于以上问题,本文提出了一种基于希尔伯特变换的相位解调算法,并以此构建了新型光纤分布式声波测量系统,在不劣化解调结果的前提下,极大地简化了相位解调OTDR系统中光路结构,并通过理论与实验证明了该系统可正确、稳定地解调外加正弦信号的幅值、频率及位置信息,实现分布式振动信号的准确测量。
1 算法原理
1.1 后向瑞利散射光的原理
参考单个脉冲周期内, 光纤后向瑞利散射光一维脉冲响应模型[11-12],假设入射光是频率为f的矩形脉冲,脉宽为w,同时假设该光源相干时间与脉宽w相比足够大。在t=0时将这样一个光脉冲发射进光纤,在光纤输入端获取后向瑞利散射光er(t),其振幅可表示为
(1)
式中:ai和τi分别是第i个散射波的振幅和时间延迟;N是设定的散射中心个数;当t-τi/w≤1时,矩形函数rectt-τi/w值为1,否则为0。时间延迟τi和从输入端到第i个散射的光纤长度li的关系为τi=2nfli/c,c是真空中的光速,nf是光纤折射率。
因此,最终得到任意时刻接收到的干涉光强为
(2)
式中,相对相位Δφij=4πfnfli-lj/c。
如式(2)所示,干涉信号包含由声信号引起的相位差φij。只需要解调φij,就可以定量地恢复声源的信号幅度、相位和频率等相关信息。
1.2 希尔伯特变换-微分交叉相乘(Hilbert-DCM)解调算法原理
从式(2)出发,每个散射中心的ai、aj可近似认为是常数,某时刻接收到的对应光纤上某位置处的干涉光强可简化为
I=A+BcosΔφ,
(3)
其中,A为直流分量,B为增益系数,Δφi为相对相位。当这一位置光纤上受到任一外待测信号ft影响时,由于干涉作用相对相位将变为Δφ=ft+φ0,其中φ0为初相位常数。
Hilbert变换可将cosθ变换为sinθ,因此当I经过去直流使得A=0时,式(3)可变化为
I=Bcos[f(t)+φ0],
H(I)=Bsin[f(t)+φ0]。
(4)
之后采用如图1所示的微分交叉相乘(DCM)算法,然后经过归一化、微分运算后输出得
I′=f′(t)cos[f(t)+φ0],
H′(I)=-f′(t)sin[f(t)+φ0]。
(5)
再经交叉相乘、积分运算后输出得

(6)
由于ψ是积分引入的缓变量或常量,可以通过高通滤波器来滤除,从而解调出待测的信号ft。
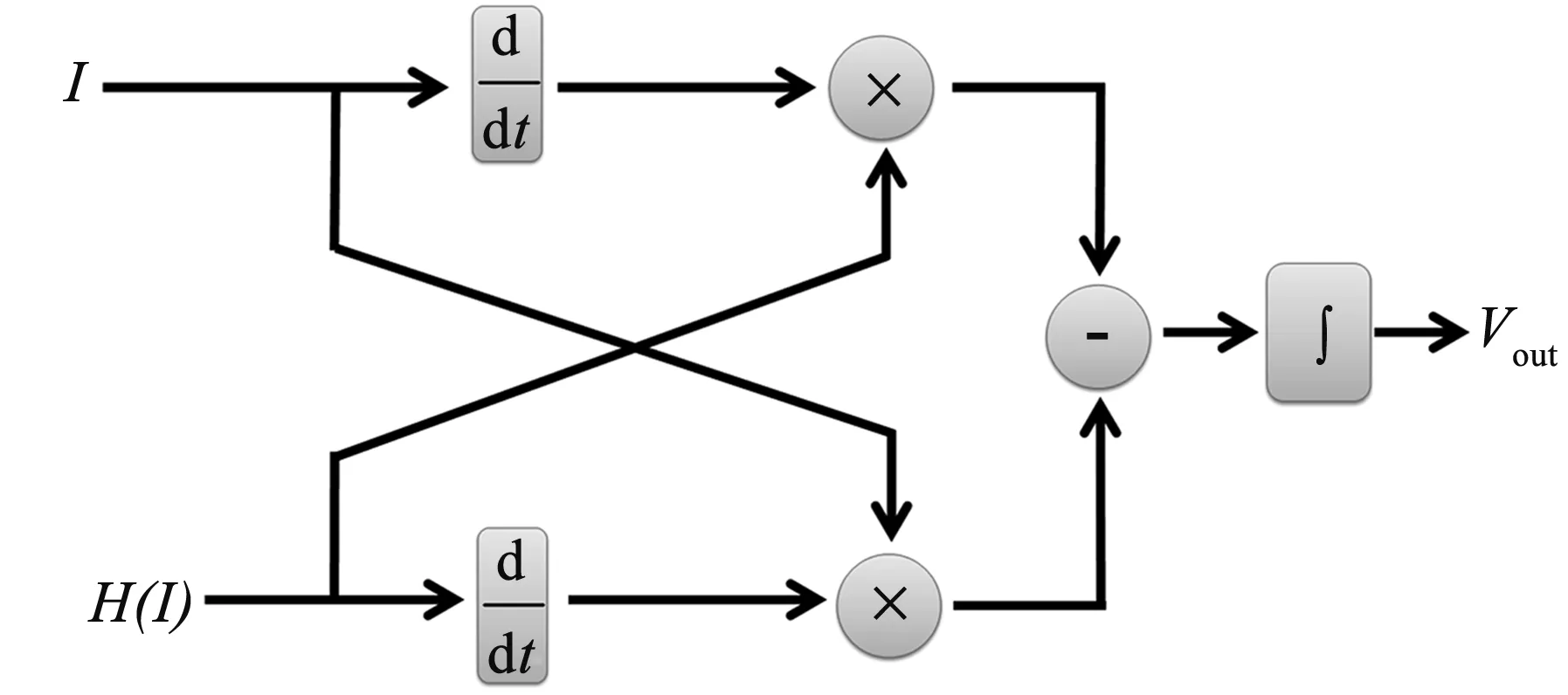
图1 微分交叉相乘解调框图Fig.1 Block diagram of differential cross multiplier (DCM) demodulation
2 实验模拟结果
首先通过Labview软件模拟信号的方法,对Hilbert-DCM算法解调的情况进行了理论模拟。式(4)中各参数定义为B=1、φ0=0.000 1,采样率20 kHz,模拟输入的待测信号ft为幅值0.1 rad、频率100 Hz的正弦信号,模拟解调结果如图2所示。可见解调信号能完整还原待测输入100 Hz信号,解调幅值较输入待测信号稍有缩小(0.075 rad)。解调信号还包含待测信号的倍频、三倍频等高频谐振峰,但谐振峰幅值与待测信号主峰幅值相比要小很多,最高的二倍频幅值也仅有2.5×10-4rad,相较于待测信号主峰可以忽略。

图2 解调100 Hz信号的时域、频域理论模拟图Fig.2 Theoretical simulation of time and frequency by demodulating 100 Hz signals
另外通过改变输入待测正弦信号ft的幅值,理论模拟了算法解调结果的线性度,如图3所示,可见输入信号幅值从0.1 rad线性增加到3.9 rad时,算法解调幅值也同样从0.15 rad线性增加到1.72 rad,说明输入信号幅值与解调幅值具有非常好的线性关系。

图3 解调线性度模拟图Fig.3 Simulation diagram for demodulation linearity
在此基础上,我们通过实验测试Hilbert-DCM算法解调真实光纤后向瑞利散射光的情况。测试系统结构如图4所示,采用窄线宽、低噪声的分布反馈光纤激光器(DFB-FL)作为光源,然后经声光调制(AOM)成脉冲,再经放大(A)和滤波(F)后入射到光纤;光纤的后向瑞利散射信号被光电探测器(PD)接收,进入计算机(PC)进行数据解调。探测光纤长度180 m,光纤中心取1 m的部分缠绕在压电陶瓷(PZT)上,被信号发生器驱动作为外声源,实验中信号发生器外加100 Hz、1 rad的正弦信号。

图4 实验光路图Fig.4 Experimental setup
将每1 m解调的时域谱图组合成三维的全纤解调时域图(图5),从图5中可明显看到光纤中心85 m附近区域解调出了特定的外信号,信号位置的时域、频域数据如图6所示,可见新Hilbert-DCM算法准确解调出了100 Hz外信号,信号幅值虽有抖动,但近似为1 rad,信噪比达到40 dB,证明新Hilbert-DCM算法可以实现分布式声波的测量。
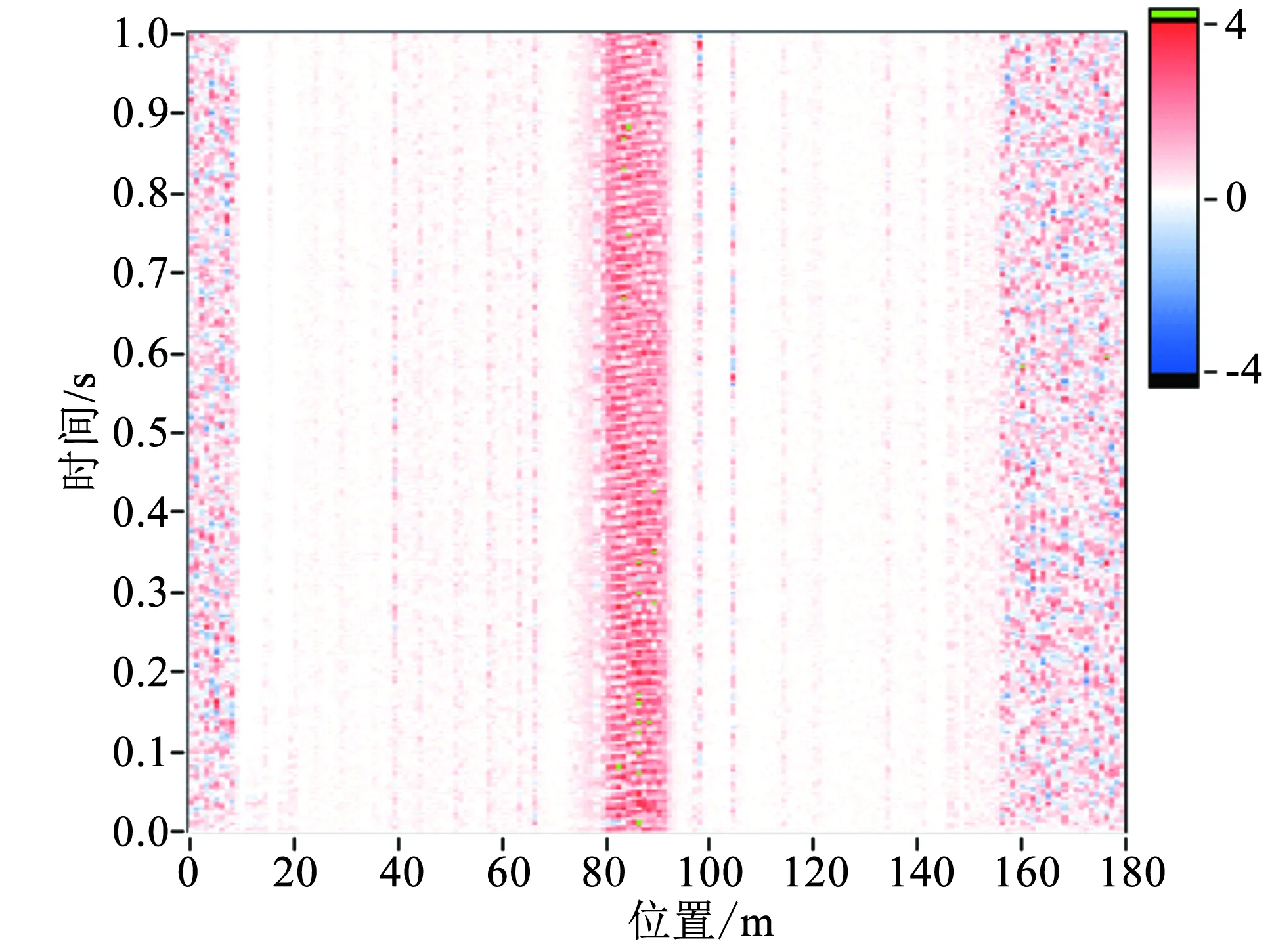
图5 全纤解调实验结果Fig.5 Experimental result of the entire fiber demodulation
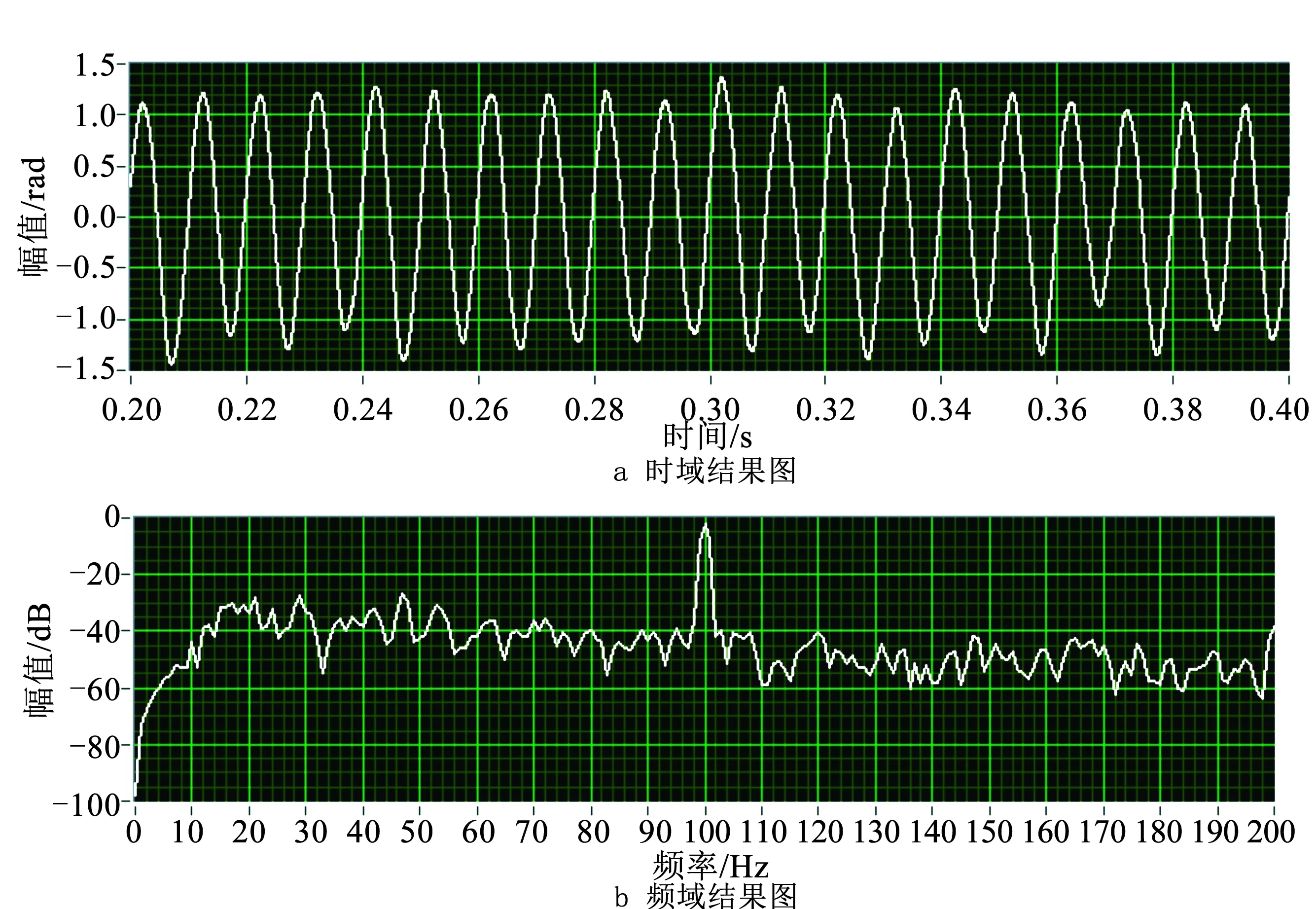
图6 解调100 Hz信号的时域、频域实验结果图Fig.6 Experimental diagram of time and frequency demodulation of 100 Hz signals
而在长时间解调稳定性上,使用相同频率100 Hz、2 rad的外信号连续解调20 s,结果如图7所示,可见除去初始由于滤波器不稳定所造成的解调幅值冲击峰,20 s内解调信号均非常稳定,与图6中1 s信号解调结果相同,达到了算法设计要求。
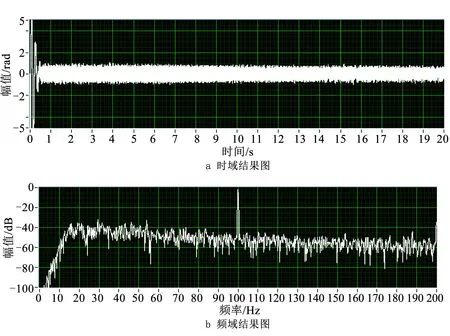
图7 解调100 Hz、20 s信号的时域、频域实验结果图Fig.7 Experimental diagram of time and frequency demodulation of 100 Hz signals for 20 s
3 结论
本文提出了一种新型希尔伯特变换-微分交叉相乘算法,在不劣化解调结果的前提下,构建了新型光纤分布式声波测量系统,相较于干涉解调的OTDR系统来说,新系统不需要外加干涉仪,仅需要1个PD采集后向瑞利散射光强信号即可进行相位解调,极大地简化了相位解调光时域反射系统中的光路结构,减小解调成本。通过理论与实验,证明了该系统在不劣化解调结果的前提下,可准确、稳定地解调外加100 Hz正弦信号的幅值、频率及位置信息,20 s长时间解调信号均非常稳定,实现了分布式振动信号的精确测量。

