巧解“一元一次方程”

徐未君 青海师范大学数学与统计学院 青海西宁 810000

法国数学家笛卡尔说：一切问题都可以转化为数学问题，一切数学问题都可以转化为代数问题，而一切代数问题又都可以转化为方程问题！虽然笛卡尔的设想未能实现，但是也充分说明了方程的重要性。方程是刻画现实世界的有效数学模型，一元一次方程是方程中最简单、最基础的部分，在数学学习中，要注意解题技巧的积累。本文介绍了几种一元一次方程的解题技巧。

一、裂相相消法

将方程中的每一项分解成两项，然后重新组合，消去一些相同项，达到简便求和的目的。

例1.解方程：

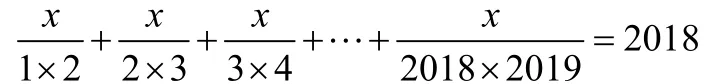
解析：上述方程的每一项都可以拆分成两个式子相减的结果，我们把每个式子拆分后，然后相加，就得到这样一个式子：

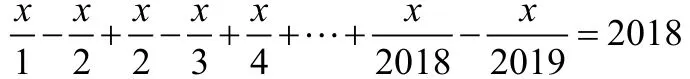
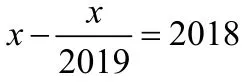
二、巧用“1”的关系

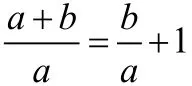
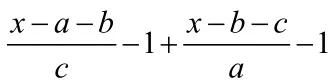
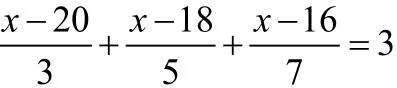
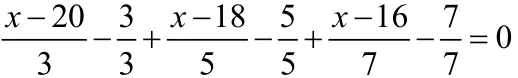
三、局部通分法：

通过观察等式两边，把有公倍数的分母的式子放在一起，进行通分，或者是带小数的方程，进行每项化简，以便于简便运算。

例4. 解方程：

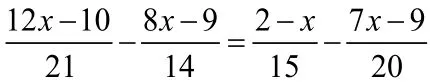
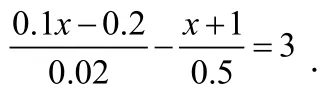
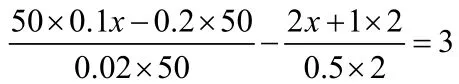
妈妈说：“把卷子拿来。”我看得出妈妈是压着气，不一会儿，彗星就要撞地球了。出乎意料地，她竟然没有打我。小兔子都到手了，狼还不下口。

四、整体通分法：

整体对方程的左右两边进行通分，如果等式两边是两个单项式，继续移项，使之左边两边分别为两个整体。

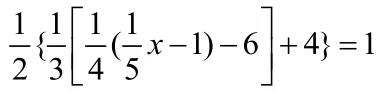
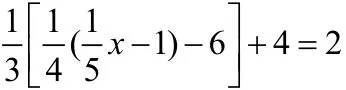
五、提取公因式法：

找出每一项的公因式，提取公因式后，进行合并，计算求解。

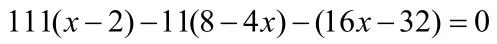
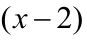
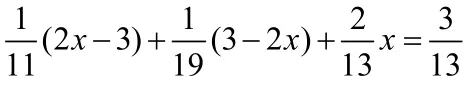
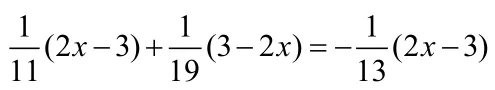
上述五种方法是在解一元一次方程时用到的重要的方法，数学题目的解题思路都是相通的，同学们要学会融会贯通，在以后的学习中，不断总结新的方法，提高学习效率。同时，掌握好一元一次方程，也为后续学习一元二次方程、一元一次不等式、二元一次方程等内容做铺垫。