关于速度合成定理两种推导法的统一性分析
杨成鹏,张娟,王佩艳
(西北工业大学力学与土木建筑学院,陕西西安710129)
0 引言
速度合成定理是理论力学教学中的重点和难点,涉及的诸多概念不仅抽象,而且相互关系错综复杂,教师讲授与学生学习都有不少困惑。关于速度合成定理的推导,文献中有两种方法,所谓的解析法[1-4]与几何法[4-7]。必须指出:长期以来,关于速度合成定理的几何法推导,争议颇多。然而,大多数理论力学教材正是采用几何法,因此这种争议会直接影响到理论力学的课堂教学。
质疑几何法的教师认为:几何法中牵连位移的概念模糊,相对速度的数学推导有误[7-9]。而支持几何法的教师则认为:几何法证明速度合成定理同样具有普遍性,而且直观、简明、易懂[4,10]。孰是孰非,问题摆在了广大教师面前。我们有理由相信这种争议会促使广大教师对速度合成定理的推证过程进行深入思考,进而改善教学。
本文将基于点的运动描述的矢量法,深入剖析三种运动(速度)的物理和数学内涵;给出速度合成定理的解析法与几何法推导过程,并阐明其求解思路的差异、模型构建的异同,以及数学表征的特殊性;根据差异性分析,论证相关概念的准确性,以及两种推证的合理性与统一性。
1 描述点的运动的矢量法
1.1 绝对运动
动点相对于定系的运动称为绝对运动,动点相对于定系的运动轨迹则称为绝对运动轨迹。先回顾一下点的运动描述的矢量法。设点P沿图1所示轨迹运动,从瞬时t到t+Δt,动点由M运动到M′,相对定系Oxyz的矢径分别为r和r′。
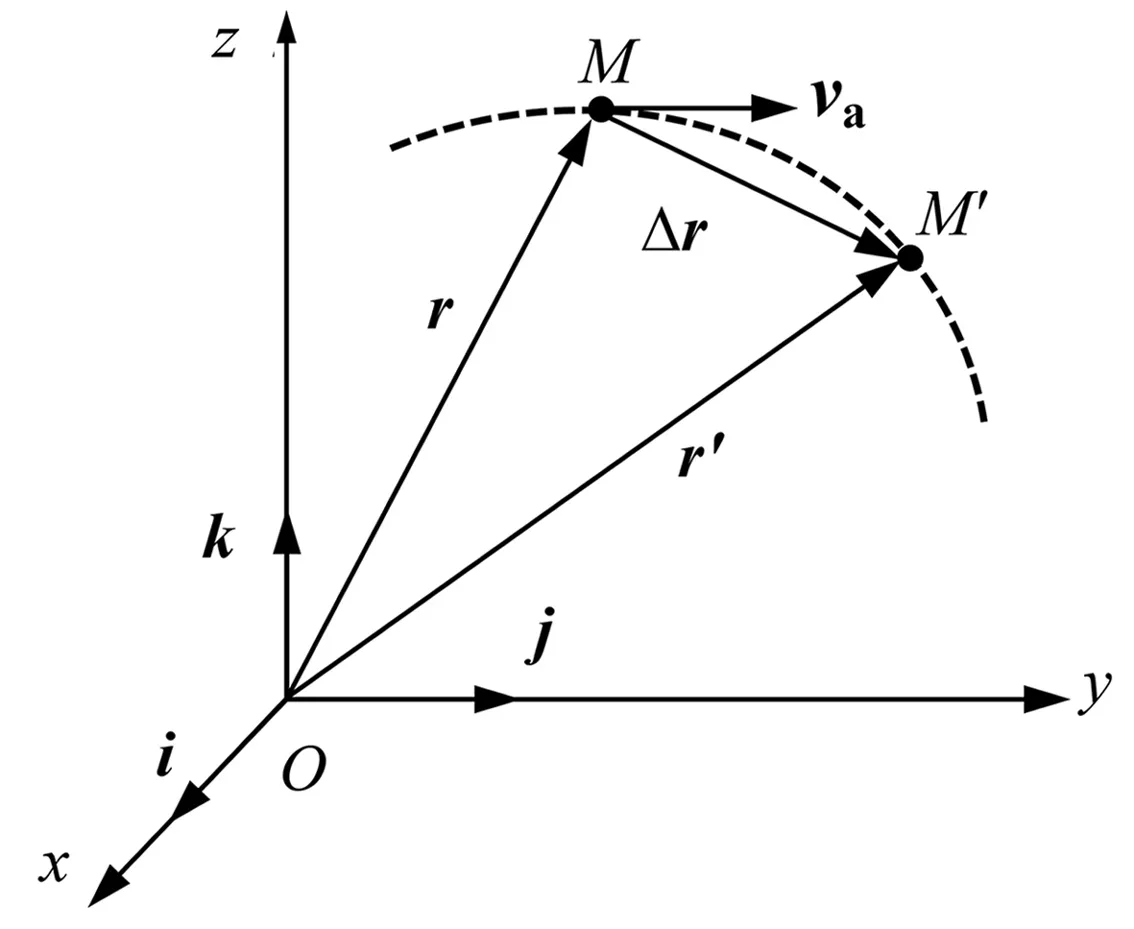
图1 定系中点的速度描述
动点P在Δt内的绝对位移可表示为
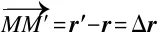
(1)
它在t瞬时的绝对速度可描述为
(2)
方向沿运动轨迹在M点的切线。应该注意,动点相对于定系之矢径r称为绝对矢径,该矢量在定系中对时间t的导数也称为绝对导数。
1.2 相对运动
动点相对于动系的运动为相对运动,动点相对于动系的运动轨迹则为相对运动轨迹。设动点P沿图2所示轨迹运动,从瞬时t到t+Δt,动点由M运动至M2,相对于动系O′x′y′z′的矢径分别为ρ和ρ′,则动点P在Δt内的相对位移为
(3)
必须指出,该位移须在动系中观测[11]。同时,给出动点在t瞬时的相对速度为
(4)
方向沿相对运动轨迹在M点的切线。注意,动点相对于动系之矢径ρ称为相对矢径,该矢量在动系中对时间t的导数称为相对导数。相对导数并不能反映动系相对于定系的运动情况。
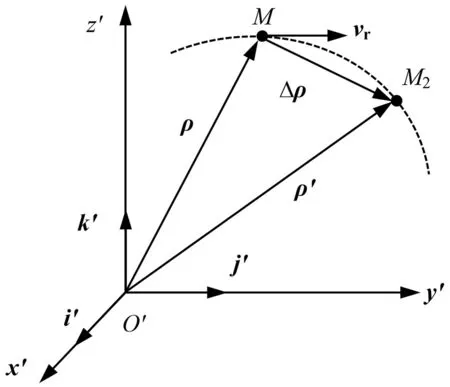
图2 动系中点的速度描述
2 速度合成定理的两种推证
2.1 解析法(运动耦合求导法)
设动点为P,定系原点为O;动系固连于某刚体;动系原点为O′,其绝对矢径为rO′;动点的绝对矢径为r,相对矢径为ρ。解析法的总体思路就是基于图3所示的矢量关系,直接求矢导数,然后根据点的运动描述的矢量法,寻求三种速度之间的关系。
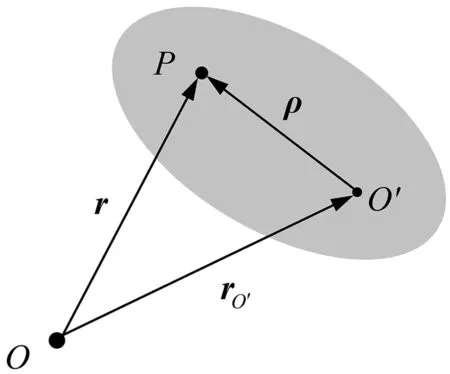
图3 矢量关系图
图示矢量满足:
r=rO′+ρ=rO′+x′i′+y′j′+z′k′
(5)
上式在定系中对时间t求导,有
(6)
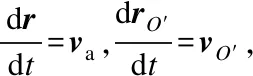
(7)
考虑到式(4)和泊松公式,得到
(8)
式中ω为动系绕O′点转动的角速度。从而得到
va=vr+vO′+ω×ρ
(9)
式中vO′+ω×ρ是动系上与动点P重合的点相对于定系的速度,即牵连速度ve。于是,可得速度合成定理的表达式
va=vr+ve
(10)
因为牵连运动为动系相对于定系的运动,所以,当动系平移时,ω=0,ve=vO′;当动系绕O′作定轴转动时,ve=ω×ρ。
2.2 几何法(运动解耦分析法)
设在t瞬时,动点处在M位置,与动系重合的点为m。假定动点相对于动系O′x′y′z′沿某一曲线(即相对运动轨迹)运动的同时,动系本身相对于定系作某种运动,经过微小时间间隔Δt,动点相对于定系由M点运动至M′点。该绝对运动可视为两个运动的合成运动,通常分解为:动点先随动系从M点运动至M1点,该过程无相对运动;后沿相对运动轨迹从M1点运动至M′点,该过程无牵连运动。相应的运动轨迹见图4。
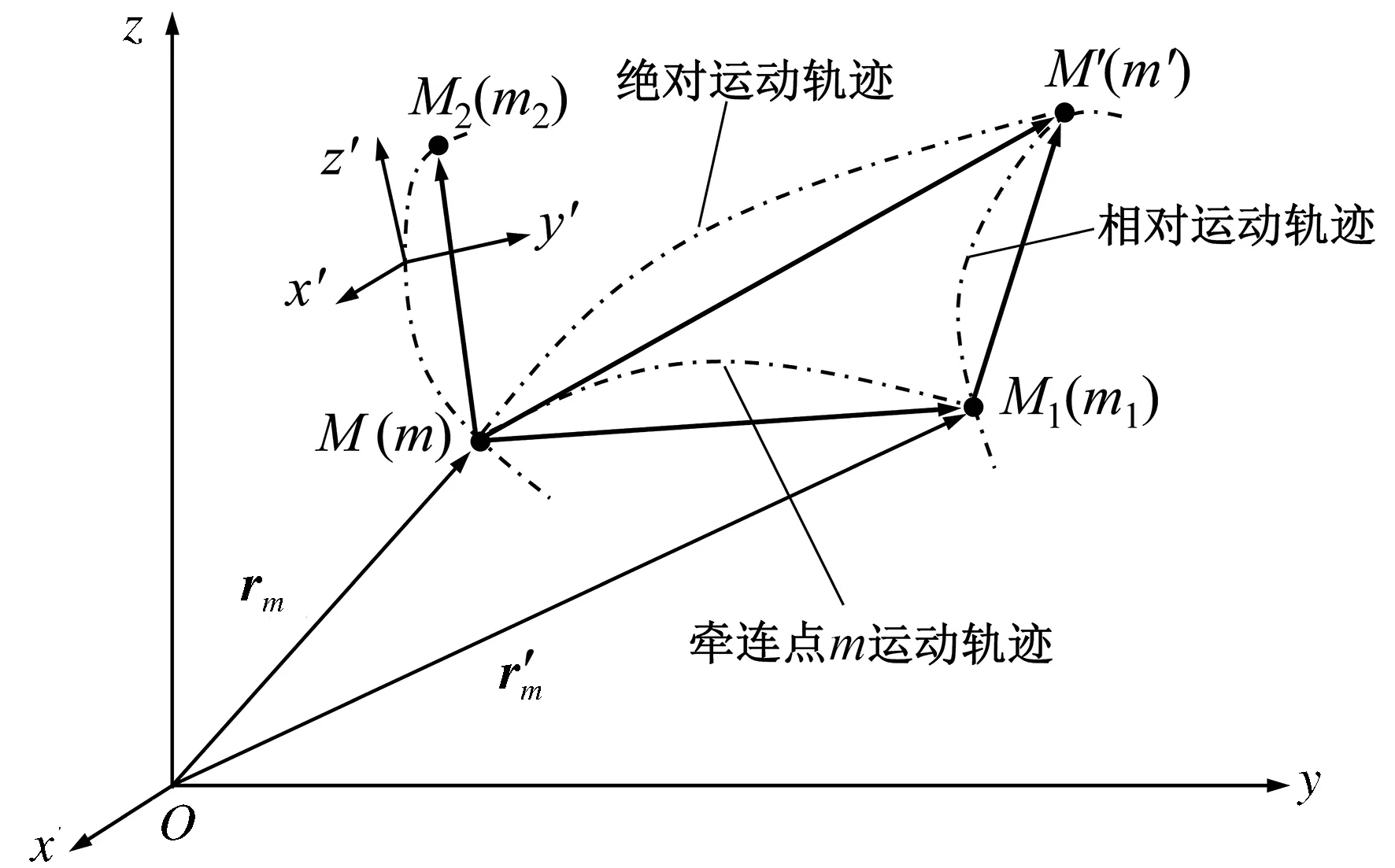
图4 运动分解示意图
下文将基于运动分解的数学内涵寻求t瞬时动点的绝对速度与相对速度、牵连速度之间的关系。
2.2.1 绝对速度
根据点的速度的矢量描述方法,若绝对矢径随时间的变化规律已知,即
r=r(t)
(11)
其矢端图即为动点的绝对运动轨迹(图4),则动点绝对速度可描述为
(12)
方向沿着绝对运动轨迹在M点的切线,指向运动前进的方向。
2.2.2 牵连速度
牵连速度即牵连点相对于定系的速度。虽然牵连点具有瞬时性,但是在所关注的t瞬时,只需研究牵连点m的绝对速度。此时,点m就是动系上一个既定的点。要求出点m的绝对速度,需要知道它的运动方程。为此,引入点m相对于定系的矢径rm,如图4所示,进而给出t时刻m的绝对速度:
(13)
即为ve,方向沿牵连点m的绝对运动轨迹在M点的切线,指向运动前进的方向。
进一步用解析法进行深入分析。牵连点的绝对矢径表示为rm=rO′+ρm,O′为动系原点,对该矢量关系式在定系中求导,有
(14)
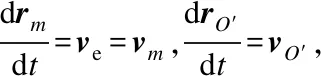
(15)
运动分解后,动点随动系从M点运动至M1点的过程中无相对运动,牵连点m相对于动系静止,即
(16)
由于动点与牵连点重合,有ρm=ρ,且vr=0,
ve=vm=vO′+ω×ρ
(17)
式(17)正是解析法得出的牵连速度之矢量表达式。
2.2.3 相对速度
动点相对于动系的速度可由相对矢径ρ的变化规律得出。假定矢量形式的运动方程已知,即
ρ=ρ(t)=x′(t)i′+y′(t)j′+z′(t)k′
(18)
根据相对导数的物理含义,给出相对速度的数学表达式:
(19)
方向必沿着相对运动轨迹在M点的切线,指向相对运动前进的方向。
(20)
不难理解,相对于动系而言,式(19)和式(20)所描述的相对速度是完全相同的。
进一步用解析法对式(20)进行深入分析。注意到,运动分解后,动点沿相对运动轨迹运动时无牵连运动影响,即动系相对于定系的位置处于设想中的冻结状态,在任意t时刻,有
(21)
此条件下,对式(5)求绝对导数,得绝对速度与相对速度vr相等;且相对矢径ρ的绝对导数与相对导数相等,为t瞬时动点之相对速度,即
(22)
式(22)具有很强的实际指导意义,即在定系中画任意t瞬时动点之相对速度矢量时,其方向沿相对运动轨迹在M点的切线。
2.2.4 速度合成
上述分析中,Δr为动点P的绝对位移,Δρ为动点P的相对位移,而Δrm为动系上m点的绝对位移,见图5。
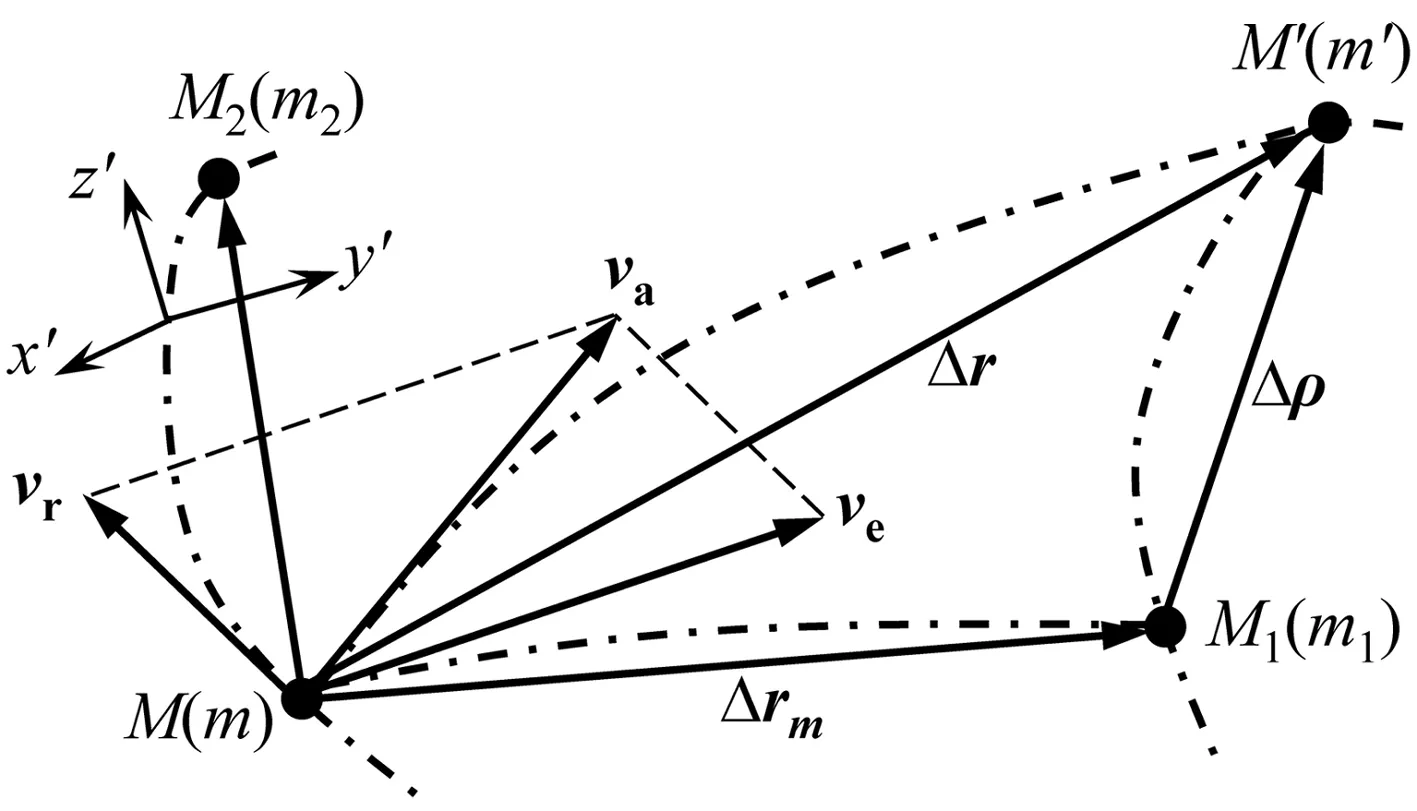
图5 速度合成图
从图5可以看出,三种位移满足:
(23)
式(23)两边同时除以Δt,在定系中令Δt→0,取极限,有
(24)
对式(24)逐项进行分析,注意到式(12)和(13),有
(25)
最后一个极限包含两层含义,即动点和动系均无限趋近于其t时刻在定系中所处的位置,同时考虑到式(22),有
(26)
从定系中看,相对速度沿相对运动轨迹在M点的切线,而绝非沿图5中的M1点之切线,因为Δt趋于零时,M1点无限趋近于M点。
至此,相对速度相对于定系和动系的大小和方向也唯一确定,从而可得点的速度合成定理。特别指出:几何法本质上是运动解偶分析法,我们认为其求解思路和极限运算是严谨的、合理的,而且论证过程直观、简明、易懂;从推证过程看出,几何法同样具有普遍性。
3 结论
1)解析法具有严谨的数学意义,涉及的概念不难理解,但推导过程和表达式比较复杂,对学生的数学思维要求比较高。
2)几何法证明速度合成定理同样具有普遍性,且证明过程直观、形象、易于理解,符合学生的认知规律和认知能力。
3)几何法与解析法的过程差异源于不同的推证思路,几何法基于运动的分解,而解析法基于矢量的求导,两种方法都是严谨的、合理的。

