基于稀疏主成分分析的图像噪声估计方法

杨 华

(南充职业技术学院 电子信息工程系，四川 南充 637000)

1 引 言

数字图像在成像、压缩和传输过程中经常会引入噪声，进而导致图像可视程度降低和信息的丢失[1-2]。为了提高图像成像质量，图像处理领域的研究者提出了多种算法[3-6]。对很多图像处理算法来说，在进行图像处理时，需预先估计图像噪声的分布模型和噪声的相关参数。

在大多数情况下，图像噪声服从高斯分布，为高斯白噪声。高斯白噪声一般为零均值。因此图像噪声估计参数一般为标准差或者方差。常用的噪声方差估计方法包括奇异值分解[7]、主成分分析[8]和小波变换[9]等。图像噪声来源主要包括传感器噪声、电路失稳、传输过程中的压缩等[10]。Li等人[11]认为图像中的信息可以被视为能量，被噪声污染之后的图像信息的部分损失可以归结为能量损失。稀疏主成分分析对数字图像这类矩阵数据的能量变化尤为敏感。在实验中，我们观察到噪声图像的高斯白噪声标准差等级与稀疏主成分分析得到的部分主成分负载向量均值呈现较为良好的线性关系。基于该规律，本文提出了一种基于稀疏主成分分析的图像高斯噪声估计方法。该方法计算复杂度低且具有较强的鲁棒性和精确性。

2 稀疏主成分分析

2.1 主成分分析

主成分分析(Principal Component Analysis, PCA)目的是在将每个样本属性值数量极大程度减小的前提下，保证原始数据矩阵的原始信息得以最大程度保留。

求解主成分(Principal Component)主要有两种方法[12]。

第一种方法利用了协方差矩阵的特性：

设有包含n个样本、p个属性值的矩阵Xn×p。

将矩阵进行中心化和标准化，标准化即每一个属性向量内的元素除以该向量内所有元素的标准差。其协方差矩阵为：

(1)

可以发现，协方差矩阵的对角线依次排列各属性方差，非对角线上的元素是所有属性两两之间的协方差。因此使用主成分分析得到的降维后的低维矩阵的协方差矩阵必须满足这两个条件：对角线元素尽可能大、非对角线元素为0。

设使用PCA对矩阵X降维得到矩阵Z，X、Z的协方差矩阵分别为C、D,P为一组正交基，有Z=XP。则有：

(2)

因此，优化目标变为寻找使得原始数据矩阵X的协方差矩阵C对角化且对角线元素从上到下降序排列的矩阵P。由于协方差矩阵为实对称矩阵，在线性代数上，实对称矩阵有一系列极有实用价值的性质[13]。若某实对称矩阵大小为p行p列，则一定可以找到p个互相正交的单位特征向量，设这p个特征向量组成矩阵E：

E=(e1,e2,…,ep)，

则对协方差矩阵C有：

取 1 mL 样品溶液加入5 mL 试剂甲混匀，于20～25 ℃放置10 min，再加0.5 mL试剂乙(Folin-酚)，立即摇匀，记录反应总体积为6.5 mL。在 20～25 ℃保温30 min，然后于500 nm 处比色，以 0 mL标准蛋白代替作空白对照。

(3)

若将特征值向量按照降序排列，每个特征值对应的特征向量矩阵E也进行对应的重排。则式(3)得到的对角阵从上到下各元素的大小也为降序排列。

因此，主成分分析所求的P就是原始数据矩阵X的协方差矩阵C的特征向量E。按照特征值大小取前K个特征值对应的特征向量按列排序，构成PCA前k个主成分对应的负载矩阵βp×k，前K个主成分为：

Zn×k=Xn×pβp×k.

(4)

第二种方法是对Xn×p进行奇异值(Singular Value Decomposition, SVD)分解：

X=UDβT，

(5)

Zn×k=UD为X通过主成分分析降维后得到的前k个主成分矩阵,βp×k为前k个主成分对应的负载矩阵，Dp×p为对角阵，对角线元素为降序排列的原始矩阵的奇异值。

上述两种方法适用不同类型数据矩阵。若以数据矩阵的每一行代表一个样本，每一列代表一种属性，第一种方法适用于样本数量远大于属性数量的数据矩阵，第二种方法适用于样本数量远小于属性数量的矩阵。

各个主成分对原数据矩阵的解释程度不同，一般通过主成分的方差贡献率(也称方差解释率)来衡量其在原始数据矩阵中所占的比重。对方法一、二，主成分的方差贡献率分别使用式(6)、(7)计算，前k个主成分的累计方差贡献率分别使用式(8)、(9)计算。

(6)

式中，λi为原始矩阵Xn×p的协方差矩阵的第i个特征值(按降序排列)。

(7)

(8)

(9)

2.2 稀疏主成分分析

稀疏主成分分析是在主成分分析的基础上，将主成分分析所得负载矩阵作为系数矩阵，与原始数据矩阵通过最小二乘法逼近主成分矩阵，同时引入L1正则化和L2正则化作为约束[14]。如式(10)所示:

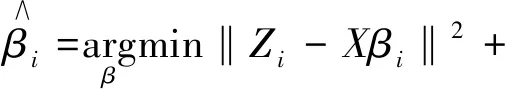
(10)

3 图像噪声估计方法

以图1所示的8幅尺寸均为512 pixel×512 pixel的灰度图进行线性关系测试。对8幅图分别添加标准差δ=5，10，20，30，…，70的高斯白噪声，使得每一幅图均对应生成8幅新的高斯白噪声图像。对噪声标准差等级δ使用多个稀疏负载向量均值的加权平均进行线性拟合，如式(11)所示。

(11)

式中，δi代表第i幅噪声图像所对应的高斯白噪声标准差等级。使用式(11)反复迭代计算之后确定r1=1,r2=5,ωj=1(j=1,2,…,5)时拟合效果最好。此时式(11)可重写为式(12)。

(12)

此时各图的拟合结果如图2所示。

在实际应用中，对单个图像而言，因未知量过多，因此式(12)无法求出唯一收敛解。为解决此问题，本文采用构造超定方程组的方式求解单个图像的未知量。方法如下所述：

设原始图像的像素矩阵为X0，添加了未知标准差等级δ0的高斯白噪声n0之后得到的新图像为X0+n0=Y0。对X0和Y0有：

D(Y0)=D(X0+n0)=D(X0)+δ02.

(13)

然后分别对Y0添加已知标准差等级δi(i=1,2,…,N)的高斯白噪声ni(i=1,2,…,N)，分别得到Yi(i=1,2,…,N)。对Yi(i=1,2,…,N)有：

D(Yi)=D(X0+n0+ni)=D(X0)+δ02+δ2i，

(14)

则结合式(12)与(14)可得到：

(15)

(16)

图1 用于线性关系测试的图像Fig.1 Images for linear relationship testing

图2 参数最优时的拟合结果Fig.2 Fitting results of the optimal parameters

N)之后生成的Yi(i=1,2,…,N)进行稀疏主成分分析所得到的第j个稀疏负载向量均值。

4 实验结果和分析

4.1 灰度图像的噪声估计

Lena标准灰度图像被用于进行噪声估计测试。文中所提出的噪声估计方法与文献[11,15]中提出的方法进行了比较。设δ0为图像高斯白噪声的真实标准差等级，δ1为使用估计方法得出的高斯白噪声标准差等级的最优估计。实验结果如图3和表1所示。

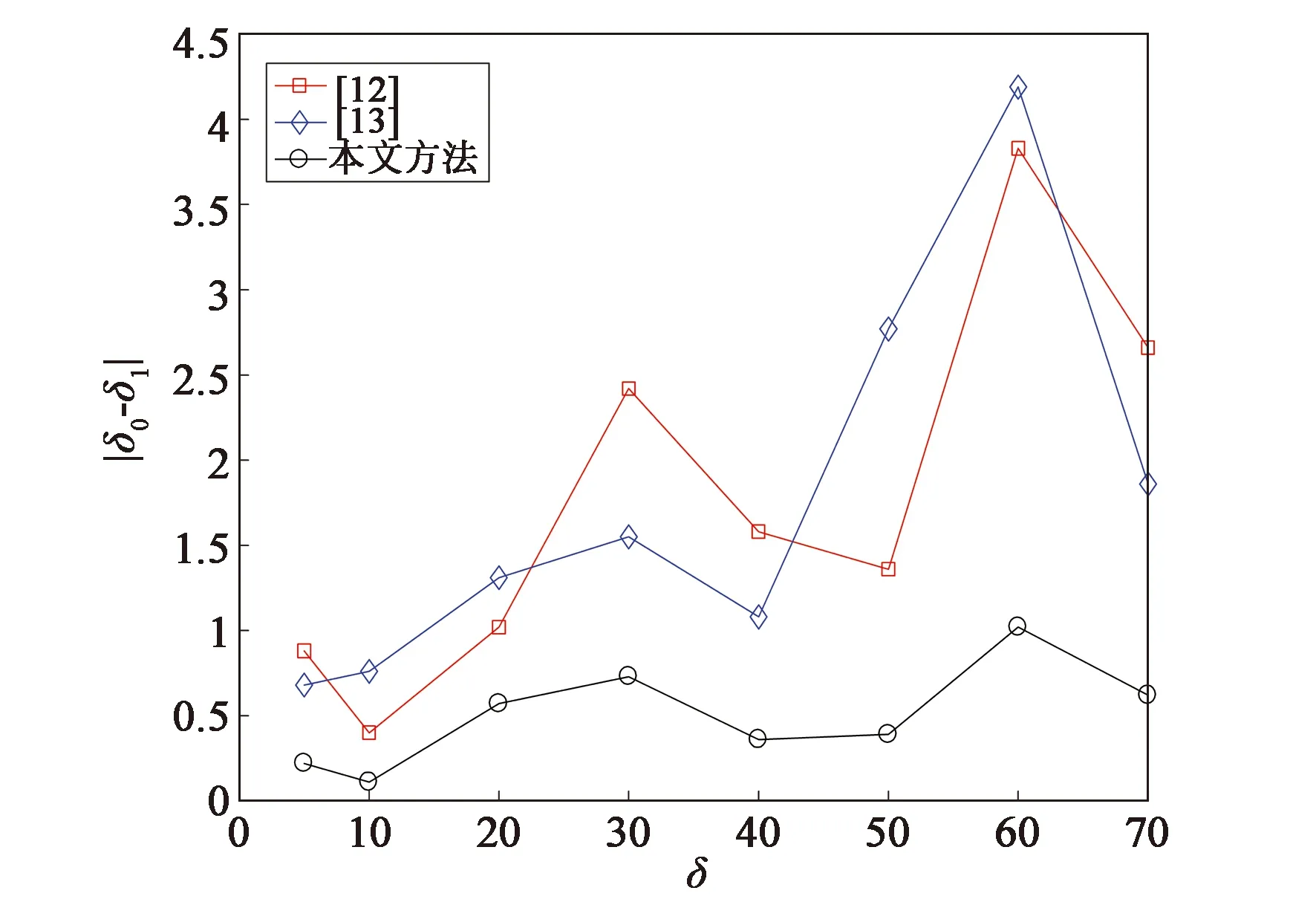
图3 不同噪声等级下3种噪声估计方法的噪声估计误差Fig.3 Estimation error of three noise estimation methods under different noise levels

从图4和表1可以看出，相比于其他两种算法，本方法的精确度更高且更具有鲁棒性。

4.2 彩色图像的噪声估计

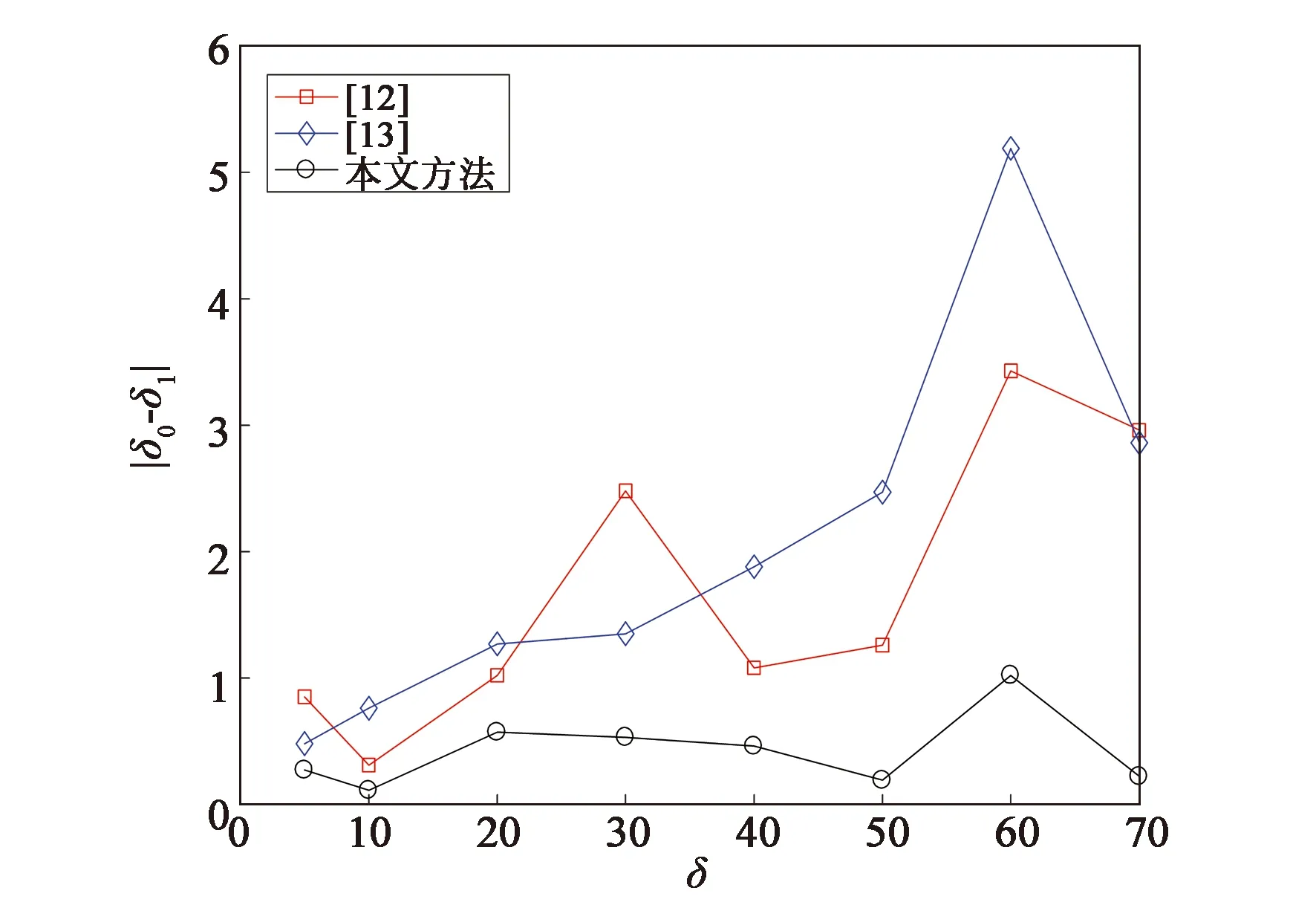
彩色图像包含R、G、B 3个像素矩阵。在实验中，分别对R、G、B 3个像素矩阵采用所提出的噪声估计方法进行噪声估计。实验所使用的Lena图像的3个通道如图4所示。与文献[11,15]的比较结果如图5和表2所示。

表1 不同噪声等级下3种噪声估计方法的估计结果

Tab.1 Estimation results of three noise estimation methods under different noise levels

δ0文献[11]文献[15]本文方法54.124.324.78109.609.2410.112021.0221.3120.573032.4231.5530.734041.5841.0840.365051.3652.7750.396063.8364.1961.027072.6671.8670.62

从图5和表2可以看出，本文方法在3个通道都达到了最高的精确度，且估计效果不受噪声等级影响。

(a)R通道(a) R channel

(b)G通道(b) G channel

(c)B通道(c) B channel图4 Lena图像的R、G、B 3个通道Fig.4 R, G, B channels of Lena image

(a)R通道(a) R channel

(b) G channel(b)G通道

(c)B通道 (c) B channel

5 结 论

高斯噪声图像的噪声标准差等级与稀疏主成分分析得到的部分主成分负载向量均值呈现较为良好的线性关系，基于此特征，本文中提出了一种基于稀疏主成分分析的图像高斯噪声估计方法。在该方法中，经过实验确定了前5个稀疏负载向量均值之和与噪声等级的线性度最优;同时通过在图像中依次添加已知噪声等级的高斯白噪声的方式构造超定方程组，在反复迭代之后求解出噪声等级的最优估计量。在标准图像Lena的灰度图和彩色图像三个通道的测试中,该方法展现出了相比于其他两种算法更高的精确度，在低噪声(δ0=5)到高噪声(δ0=70)条件下均具有较高的估计精度和较强的鲁棒性，具有一定的工程实用价值。