基于PSF重构和改进的最大后验估计的自适应光学图像复原算法

武兴睿

(吉林科技职业技术学院，吉林 长春130123)

1 引 言

在自适应光学(AO)图像处理中，对无波前测量数据的 AO 图像进行后处理，得到高清晰图像。但由于受大气湍流的影响，这些 AO 图像的点扩散函数(PSF)很难确定，因此必须根据观测图像，联合估计目标图像和点扩散函数来进行复原，即盲图像复原技术[1]。Ayers等人提出了基于单帧的盲去卷积方法[2]，该方法对噪声敏感而影响图像的复原效果；Tian等人提出了一种基于帧选择和多帧盲去卷积方法的AO图像复原[3]，帧选择技术有利于提高复原质量；张丽娟等人提出了一种基于改进最大期望的多帧迭代去卷积算法的AO图像复原方法[4]，该方法建立代价函数并估计正则项，但其计算速度较慢；Yap等人提出了一种基于神经网络架构的自适应图像复原方法[5]，该方法的主要优点是优化的正则化向量和局部感知测度之间的经验关系可用于其他退化图像的复原，算法的主要局限性是其收敛速度。

为了提高自适应光学图像的分辨率，本文通过寻找最合适的图像数据集来进行联合最大后验估计(JMAP)，同时估计PSF和目标图像，解决盲去卷积问题。

2 问题描述

2.1 AO图像观测模型

盲去卷积描述如下：

g(x,y)=f(x,y)⊗h(x,y)+n(x,y)x,y∈Ω

，(1)

式中，f(x,y)表示原图像，h(x,y)表示点扩散函数，g(x,y)表示采集到的降质图像，n(x,y)表示噪声，Ω表示图像的区域，⊗表示二维卷积符号。

在实际观测过程中，可以采集同一目标的多帧AO图像。定义多帧AO图像退化模型为

gm(x,y)=f(x,y)⊗hm(x,y)+
n(x,y),1≤m≤M，

(2)

2.2 PSF重建方法

本节提出的PSF重建方法属于模型估计方法，将考虑退化原因，包括大气湍流模型，自适应光学系统的参数等[6]。

为了简化公式，本文使用一维模式描述AO图像。理论上， AO系统闭环校正后的PSF数学模型[6-7]为：

(3)

由于AO系统的焦距误差或光学偏差，瞳孔函数应修改为：

p(u)=P(u)ejθ(u)，

(4)

式中：θ(·)是由聚焦误差或光学偏差引起的波前相位误差。

PSF模型可定义为：

(5)

由式(5)可知，PSF依赖于θ(·)。由于大气湍流的影响，相位误差会随时间而变化，因此定义随时间变化的PSF模型：

(6)

式中，θt(.) 是由随时间变化的大气湍流引起的相位误差。

3 AO图像复原的关键算法

大量的盲去卷积工作主要来源于天文学[8]。盲去卷积方法同时对PSF和目标图像进行联合估计，本文提出的联合估计基于贝叶斯框架的MAP估计方法，即

(7)

式中：p(g,f,h;θ)表示原图像g，观测图像f和PSFh的联合概率密度。

光学图像的噪声主要服从泊松分布的光子噪声[8]。AO图像以强均匀背景为主，这种情况下，假设短曝光AO图像噪声为服从高斯分布的白噪声，其方差为σ2。对于目标图像，选择一个具有协方差矩阵为Rf，均值为fmean的平稳高斯分布，如式(8)所示：

(8)

式中：N2表示图像像素的个数，det(Rf)是矩阵x的行列式，H是PSFh的卷积算子。

因此，可以定义估计目标的代价函数：

J(f,h)=-ln(p(gf,h;θ))-
ln(p(f;θ))，

(9)

式中：第一项是数据保真项，第二项是正则化项。由式(8)，根据最小化准则求解式(9),即：

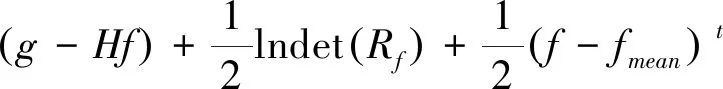
(10)

式中，C是常数。

采用共轭梯度法完成这种最小化任务，最小化式(10)，得到了提出的迭代算法对目标和点扩展函数的估计，即：

(11)

(12)

下面的步骤描述了本文提出的AO图像复原算法，具体过程如算法1所示。算法1给出了该算法的实现过程。

算法1 本文复原算法实现的步骤 Step 1:初始化操作。采用帧选择技术[3]选出M帧AO图像(g1, g2,…, gM),以f︿0=g1+g2+…+gM()/M。Step 2:根据节2.2的算法,获取PSF的初始估计h︿0。

Step 3: 迭代计算j=1, 2, …, Max_iteration (Max_iteration=100 或 200)。(1)PSF的内循环计数变量h_ count=0。(2)PSF估计的迭代过程,p= 0,1,…, Max_count。(a) 基于共轭梯度法优化式(12),完成PSF估计h︿(p);(b) h_ count++; p++;(c) 检查循环变量 p 的值, 如果 p< Max_count,则继续循环; 否则,转Step 3 (3)。(3) 标估计内循环计数器变量:f_count=0。

(4)目标估计的迭代过程: q=0,1,…, Max_count。 (a) 采用共轭梯度法优化式(12),实现目标图像估计f︿(q);(b) f_count++; q++;(c) 检查循环变量 q, 如果 q< Max_count,则继续循环; 否则,转Step 3(5)。(5)检查外循环是否结束, 如果 j> Max_iteration, 则转Step 4。(6) j+ +, 返回到 Step 4(1)。Step 4:算法结束。 如果j >Max_iteration, 输出估计图像f︿,结束算法;否则转Step 3。

4 仿真实验结果与分析

4.1 客观评价

由于缺乏理想图像参考，本文采用峰值信噪比(PSNR)[9]和拉普拉斯梯度模 (LS)[10]作为客观评价准则。PSNR定义：

(13)

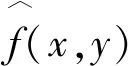
LS定义为：

(14)

4.2 仿真AO图像复原实验

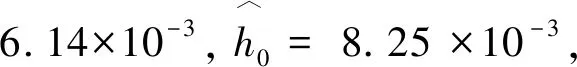
图1 原图像及降质图像序列Fig.1 Original images and the multi-frame degraded images

图2 复原算法比较Fig.2 Comparison for image-restoring methods

采用客观评价标准PSNR 、LS和计算时间比较本文算法与其他3个算法(Wiener-IBD算法，RL-IBD算法及FS-MLJD算法)进行客观实验比较，结果如表1所示。以“Man”图像为例，与Wiener-IBD算法，RL-IBD算法及FS-MLJD算法相比，本文算法的PSNR测度分别提高了6.83%、4.47%和2.28%，LS值分别提高了22.2%、17.9%和12.1%。在表1中可以看出，本文算法可以获得更高的PSNR和LS。但是该算法的计算量略高于其他3种复原算法，所以下一步需要提高算法的性能。

表1 不同复原算法的PSNR， LS及计算时间3项评价指标比较结果Tab.1 Comparison results on PSNR, LS and Computation time of different restoration algorithms

从视觉上和客观的评价都可以看出，本文方法可以有效地复原降质的AO图像，并且复原后的AO图像质量有了明显的提高。

5 结 论

针对自适应光学图像的特点，本文提出了一种基于改进的最大后验估计法的自适应光学图像复原算法，还提出了基于波前相位信息的点扩展函数重建方法。通过对一组模拟的AO图像进行复原实验，与盲去卷积算法Wiener-IBD、RL-IBD及FS-MLJD 3种算法进行了比较。以“Man”图像的复原结果为例，与上述3种算法相比,本文算法的PSNR测度分别提高了6.83%、4.47%和2.28%，LS值分别提高了22.2%、17.9%和12.1%。实验结果表明，本文提出的AO图像复原方法在一定程度上实现了高质量的修复效果。