矿用汽车纵臂断裂失效分析与结构改进

王 辉(成都大学 机械工程学院， 四川 成都 610106)

0 引 言

汽车悬架系统的主要作用是用来缓和车辆在行驶中所受路面的冲击与振动，保证车辆具有良好的行驶平顺性和操纵稳定性[1].矿用汽车的自重比较大，满载时其质量可达千吨，由于其经常工作在崎岖不平的路面上，长期受到外部载荷的冲击，一旦其前桥结构件因选材、设计、制造等方面的不足，就会导致悬架的变形甚至断裂失效，将极大地影响到车辆行驶的安全.目前，利用ABAQUS有限元分析软件不仅能够计算悬架结构件的静力学性能，还可以精确地模拟汽车前桥零部件在转动的过程中所产生的动态力学性能.基于此，本研究针对某单纵臂悬架矿用汽车的试验样车纵臂断裂失效的情况，利用ABAQUS有限元分析软件对处于动态冲击下的矿用汽车前桥单纵臂的受力变形情况进行了分析，并对其结构进行了相应改进.

1 前桥纵臂断裂失效分析

某矿用汽车单纵臂悬架前桥的结构如图1所示.图1中，主销4的中间部位与纵臂2的圆柱筒通过锥面过盈配合，主销内倾角由纵臂2的圆柱筒来保证，纵臂2可以绕着与车架固联的销轴3上下转动；悬挂缸1的一端通过铰链与车架连接，另一端通过铰链与主销4上面的端盖连接；主销4的上下端与转向节6相连，转向节6可以绕着主销4的中心线旋转，从而带动转向节6上的车轮5左右转动.由于单纵臂悬架前桥结构左右对称，因此，本研究取其左边1/2作为分析对象.

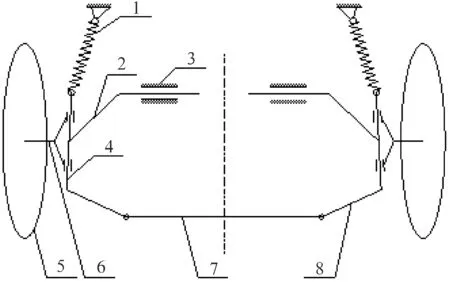
图1 单纵臂悬架前桥结构示意图

作为分析对象的某单纵臂悬架矿用汽车样车前桥的左纵臂实拍如图2所示.其结构是由纵臂铸件和纵臂钢板焊接件两部分组成，中间折弯的地方是焊接的分界线.

图2 矿用汽车纵臂部位实拍图

该矿用汽车样车在行驶试验的过程中出现纵臂断裂的情况，断裂位置发生在纵臂铸件上(见图3)，纵臂铸件在与主销的连接处断成了两半.从图3(a)可以明显的看出其铸造质量较差，断口面不仅有较大的不规则的气孔，还含有丝线类的杂质.其中，气孔的存在减小了金属的有效承载面积，使得应力集中，增大了缺口的敏感性，造成了金属材料的强度下降和抗疲劳能力的降低，成为零件断裂的裂纹源[2]；而丝线类等杂质的存在则极大地破坏了金属材料的连续性，降低了材料原本的强度和塑性.一般来说，金属材料的断裂失效可以分为韧性断裂失效、低温脆性断裂失效、疲劳断裂失效、蠕变断裂失效和环境破裂失效等[3-5].从图3(b)可以看到，失效的纵臂铸件断口较为平齐，断裂方向与正应力的方向垂直，断裂面处较为光亮，经判定为金属材料的脆性断裂.通常，金属材料脆性断裂失效的原因一般不是因为过载而是因为冲击所造成的[6].

图3 纵臂断口图

2 改进前模型的建立及有限元分析

2.1 改进前单纵臂悬架三维模型的建立

本研究利用Solidworks软件，建立起单纵臂悬架的实体模型如图4所示.

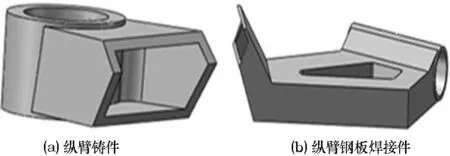
图4 悬架纵臂的模型结构示意图

图4中，纵臂模型是由纵臂铸件图4(a)和纵臂钢板焊接件图4(b)焊接而成.为了在有限元软件中进行有效地分析，对模型做了必要的简化：忽略了焊接缝隙的大小和销轴轴套的影响，以及倒角、倒圆等特征，以避免在进行有限元网格划分时，因小特征产生过多的有限元分析单元，使得结构分析精度降低.所建立的单纵臂悬架三维模型如图5所示.

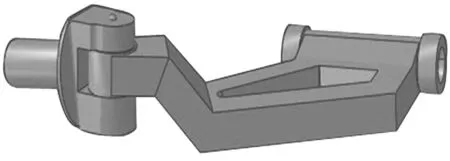
图5 单纵臂悬架三维模型示意图

2.2 材料选择与网格划分

2.2.1 材料选择.

通常，对于要给焊接在一起的零部件赋予不同的属性，需要先把焊接后的部件作为一个整体导入，在焊接的部位进行分割，然后再对分割的部分分别赋予不同的材料属性，继而才能做进一步的处理.本模型中，悬架的纵臂铸件选用35#钢，钢板焊接件选用Q345A钢，所选材料具体的参数如表1所示.

表1 纵臂材料的选择

在动力学分析中，由于悬架所受到的冲击载荷比较大，容易出现塑性变形.因此，在ABAQUS中还必须把名义的应力和应变转换为真实的应力和应变，并据此定义材料的塑性特性数据[7].

2.2.2 网络划分.

在选用ABAQUS软件进行网格划分时，本研究的生成算法选用在可靠性、几何通用性和效率上都较好的四面体网格，并在不同的部位对网格的大小进行合理控制.所建立的单纵臂前桥的有限元网格模型如图6所示.通过Mesh→verify网格检查高亮显示，得知网格划分较好.

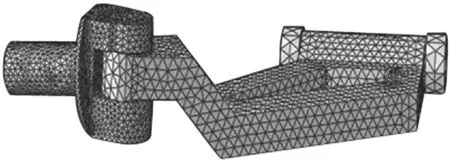
图6 单纵臂前桥的有限元网格划分模型示意图

2.3 弹塑性力学分析

2.3.1 满载冲击工况.

满载冲击工况主要是用来模拟矿用汽车在满载直线行驶时遇到路面高低不平对纵臂所产生的冲击情况.路面的不平度可以用脉冲输入来近似模拟，主要有三角形凸块和长方形凸块两种[8].对于满载超百吨级的矿用汽车，一般选取长方形凸块的脉冲输入，将其长度设定为5 000 mm，高度设定为100 mm.当矿用汽车以50 km/h的速度通过时，所采用的路面不平度可按式(1)计算，

q=(100/2)·sin(pi·x/5 000)

(1)

式中，x为分割的数量，得到在采样时间为0.01 s时，等距离间隔为36，位移等距离间隔(5 000/36 mm),从而得到每个采样时间所对应的路面不平度q值的大小.按照等比例变换，就可以得到脉冲应力变化所需要的幅值如图7所示.

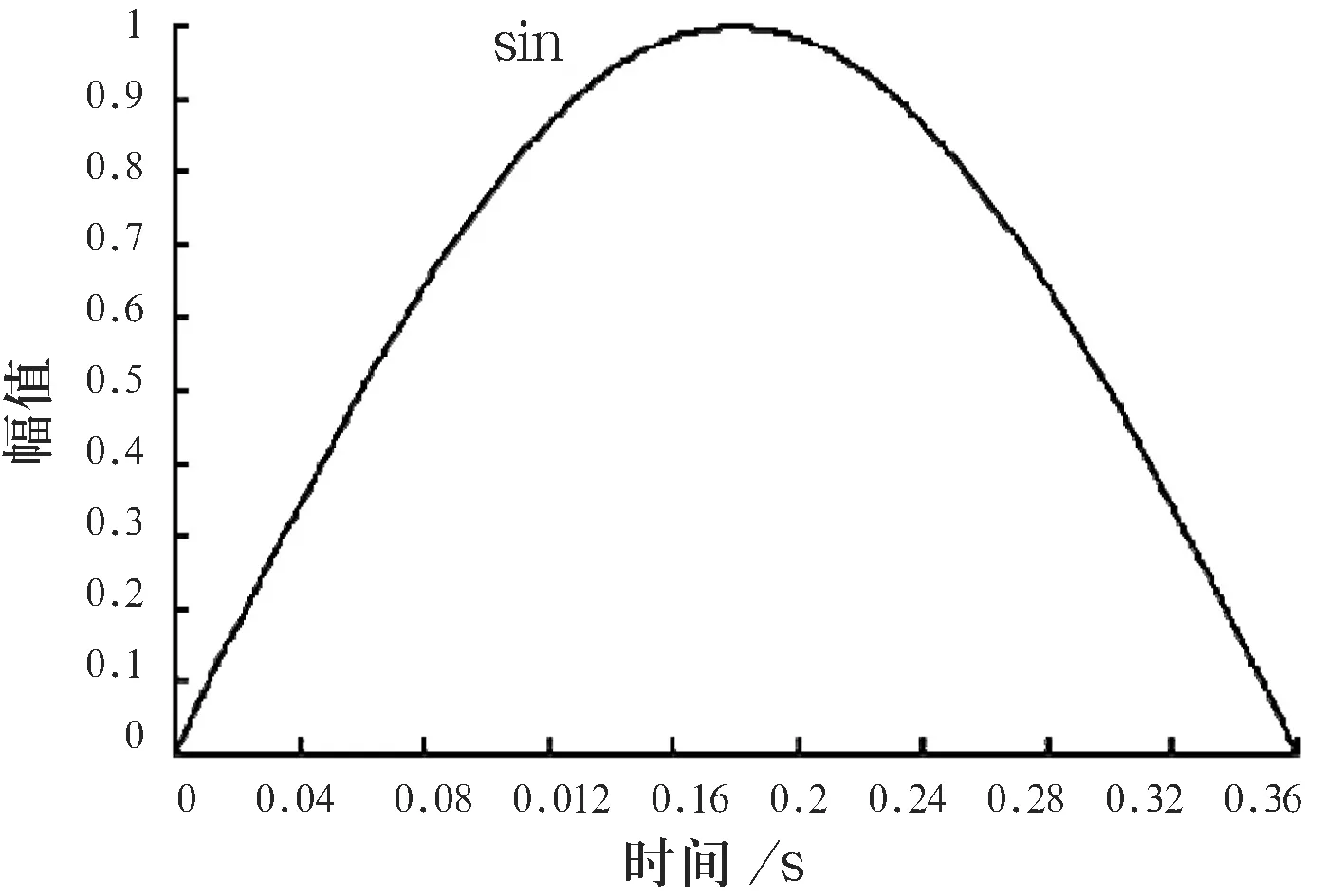
图7 模拟脉冲变化幅值曲线

研究的矿用自卸汽车在满载时单个纵臂要承担的载荷为50 t.在进行外力加载时，需要将该载荷在0.36 s的时间内加载到转向节臂上，由此分析纵臂的受力变形情况.在路面的冲击作用下，纵臂的应力值大小随着时间增加而不断变化.经过数据处理，得到悬架纵臂所受的最高应力随冲击时间的变化曲线如图8所示.

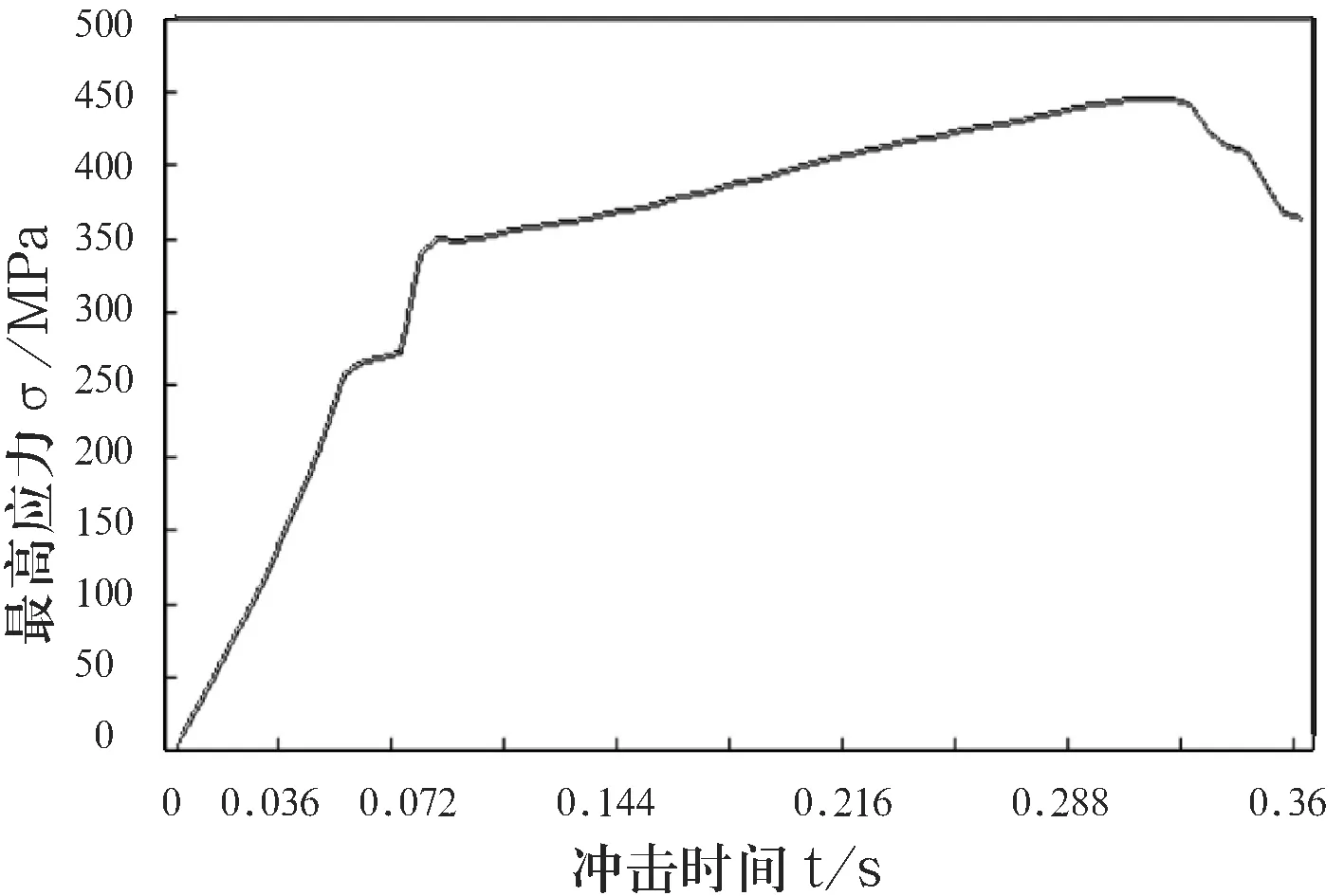
图8 纵臂所受的最高应力随时间的变化曲线

由图8可以看出，纵臂受到的最大的冲击应力约为445 MPa.而应力值已大于纵臂铸件与焊接件的屈服极限，两种材料均出现了塑性变形.

在0.318 s时，纵臂所受应力的分布情况如图9所示.此时，其最大应用为445.5 MPa,可见，当矿用汽车处于满载冲击工况时，比较危险的区域为纵臂焊接件折弯处以及纵臂与销轴连接的转动区域处.前桥零部件最大应力出现的部位则是在与转向节相连接的纵臂铸件的上下表面以及转向节与主销连接的区域.在实车试验时，在纵臂铸件处出现了断裂.分析结果与纵臂断裂失效的部位一致.

图9 t=0.318 s时纵臂应力分布情况

2.3.2 动态左转向至极限工况.

动态左转向至极限工况，是用来模拟汽车在满载直线行驶时，突然向左打方向盘，车轮转角的变化对纵臂的影响.当矿用汽车向左转向时，此时前桥的左前轮为内转向轮，最大转角为39°.将总的分析时间设定为4 s，第1 s，转向节不动，将满载载荷施加在转向节臂上，剩余的3 s是转向节开始转动的加载时间，由此可以得到纵臂所受的最高应力随时间的变化曲线如图10所示.

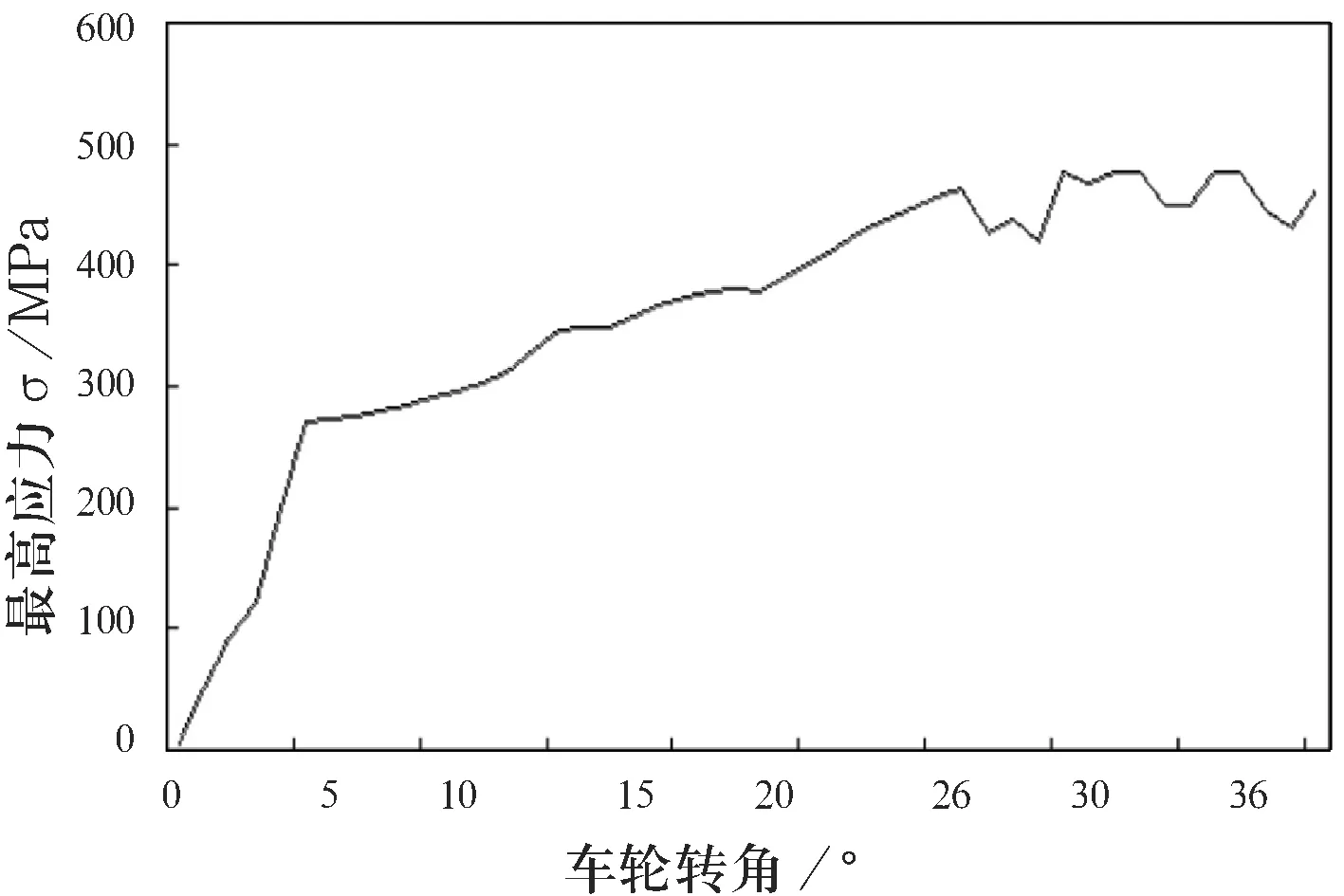
图10 左转向时，纵臂所受的最高应力随转角变化曲线

由图10可以看出，纵臂随车轮转角的变化所受到的最大应力为456 MPa. 此时，作用力臂最长，作用力矩最大.在纵臂铸件和纵臂焊接件材料的屈服极限处均出现了突变，说明材料的弹塑性能在纵臂的受力过程中起到了非常重要的作用.

在左转向至极限的工况中，矿用汽车纵臂最大塑性应变随转角的变化曲线如图11所示.

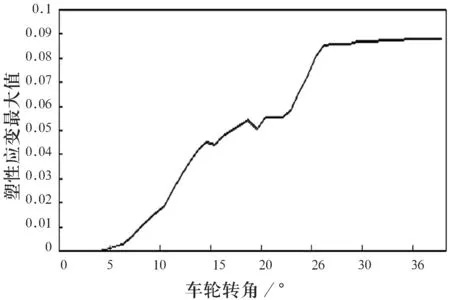
图11 纵臂最大塑性应变随转角的变化曲线

由图11可知，当应力值大于纵臂铸件的屈服极限后，纵臂铸件和焊接件均发生了较为明显的塑性变形，在车轮转角超过36°后，塑性应变不再发生变化，材料开始进入到硬化阶段.

当转角为29°时，纵臂所受的应力的分布情况如图12所示.

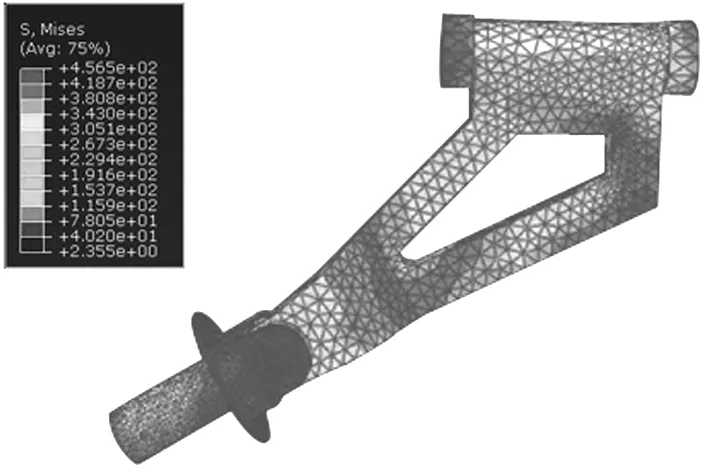
图12 当转角为29°时，纵臂应力分布情况

由图12可知，纵臂所受的最大应力发生的部位同矿用汽车满载行驶所受到的路面的冲击情况相类似，因此，在纵臂的设计过程中要重点考虑所涉及的几个区域的刚度与强度的影响.

2.3.3 动态右转向至极限工况.

动态右转向至极限工况，是用来模拟汽车在满载直线行驶时，突然向右打方向盘，车轮转角的变化对纵臂的影响.当汽车右转向时，此时前桥的左前轮为外转向轮，最大转角为27°.在进行数据处理时，只需要将左转向分析时所设定的换算角度改为右转向时的换算角度，同时改变符号，表明方向不同.其余的约束及加载不发生变化.重新进行分析计算，可以得到纵臂在右转向时所承受的最高应力随时间变化的曲线如图13所示.

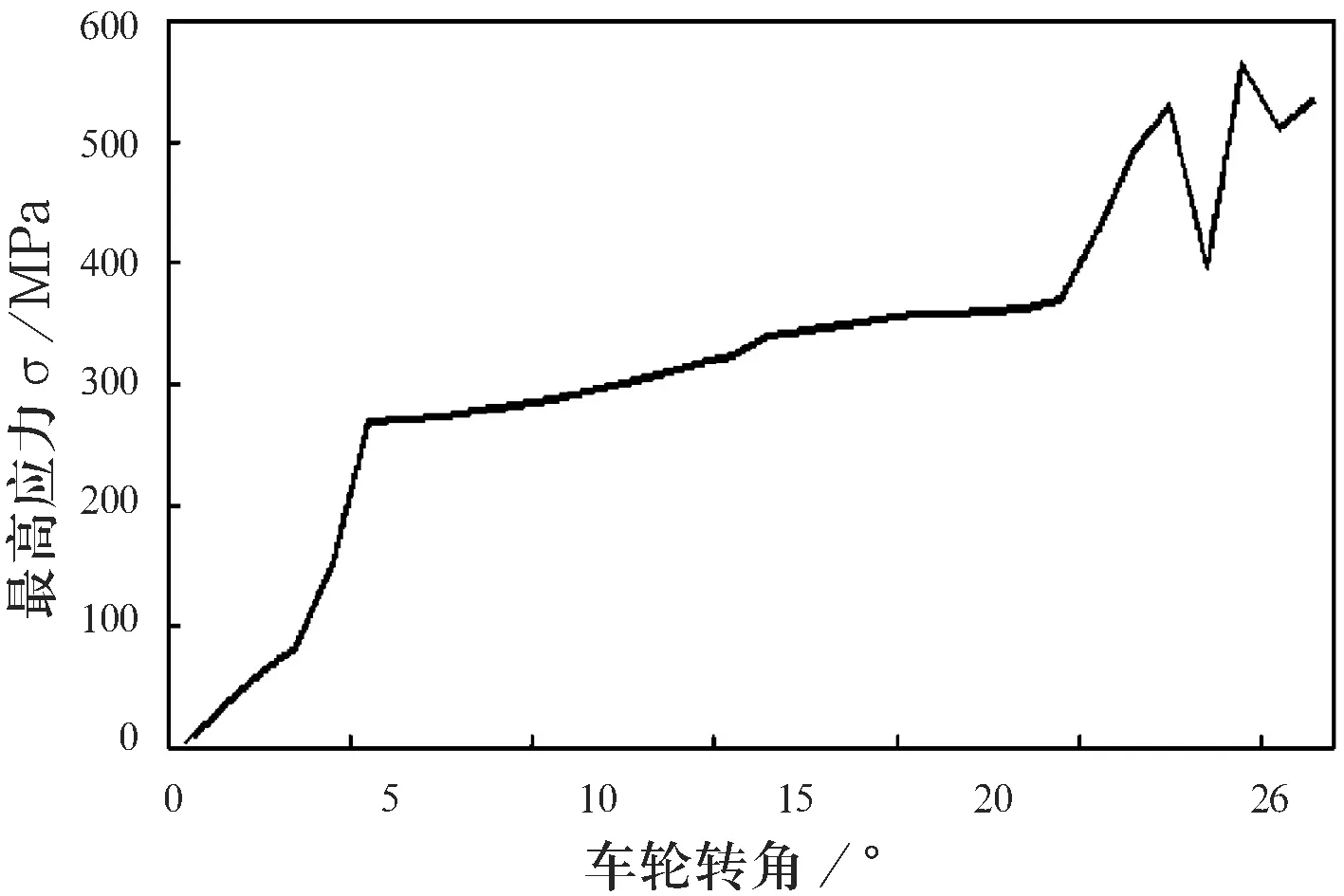
图13 右转向时，纵臂所受的最高应力随转角变化曲线

从图13可以看出，纵臂随车轮转角的变化所受到的最大的应力值为565 MPa.出现这么大的应力集中，主要原因还是在转向节向右转动的过程中与纵臂的结构形成了一定的相互干涉，造成了应力的瞬时增加.

在右转向至极限的工况中，矿用汽车纵臂最大塑性应变随转角的变化曲线如图14所示.

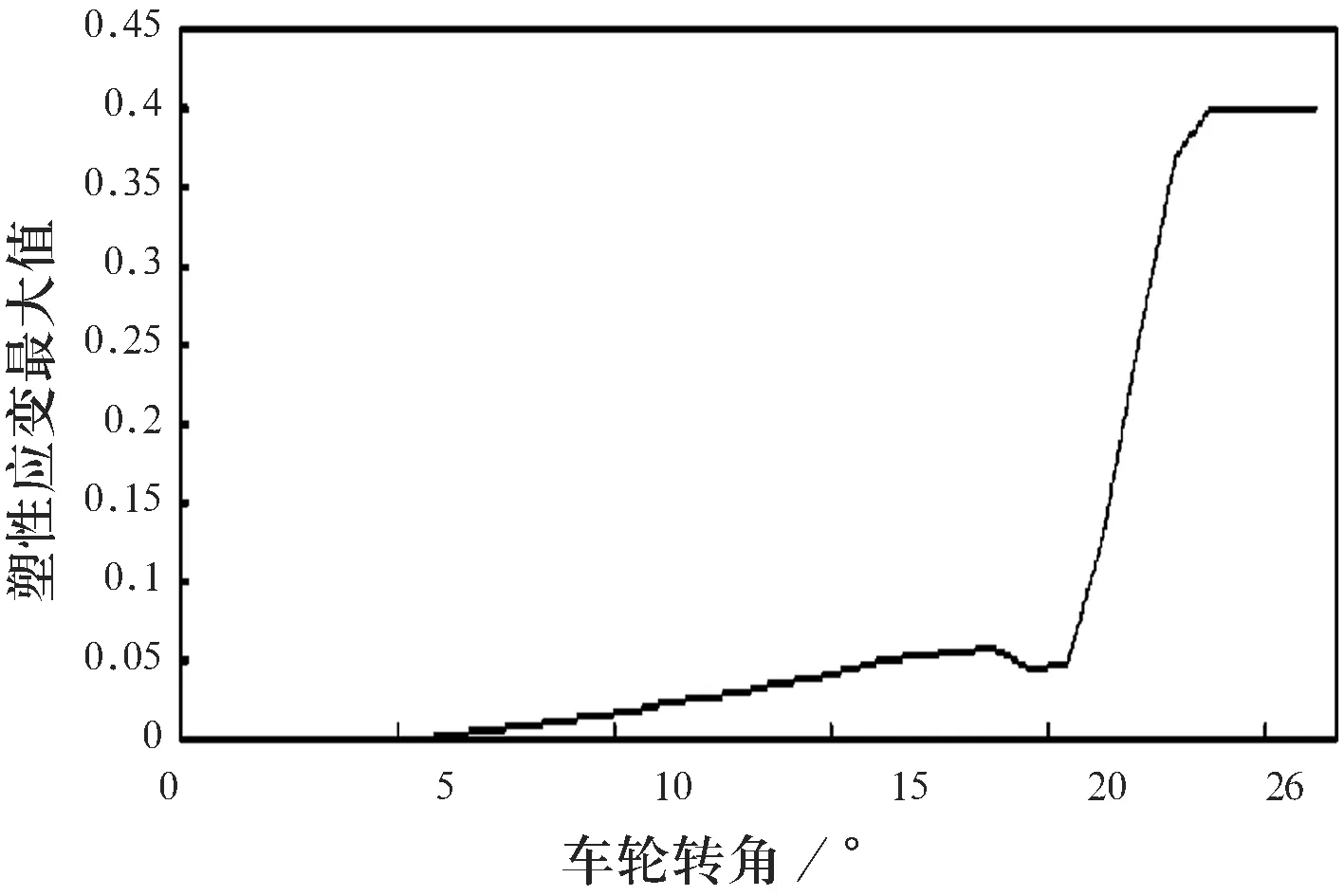
图14 悬架的最大塑性应变随转角的变化曲线

由图14可知，当应力值大于纵臂铸件的屈服极限后，纵臂铸件和焊接件均发生了较为明显的塑性变形.右转工况同左转工况相比，纵臂塑性应变的数值明显要大很多.

将应力的最小值设定为纵臂铸件的屈服极限，最大值设定为纵臂焊接件的屈服极限，可以得到纵臂在转向节转角为25°时应力的分布情况如图15所示.

图15 转角为25°时，纵臂应力分布情况

从图15可以看出，在转向节和纵臂连接的上表面以及纵臂和主销连接的侧面均出现了较大的应力集中，应力集中发生的部位与纵臂断裂的部位一致.

3 改进后模型的建立及有限元分析

3.1 改进措施

通过对纵臂断口的宏观观测以及ABAQUS软件对单纵臂悬架的有限元分析可知，矿用汽车前桥结构件的刚强度与选择的材料、加工的质量以及具体的设计方案密切相关.在实车前桥纵臂发生断裂失效后，需要对前桥的结构件尤其要对纵臂断裂的部位加以改进，本研究采取的改进措施包括：

1)在整车允许的范围内，抬高纵臂的整体高度，提高纵臂的抗弯和抗扭的能力；

2)通过优化分析，找到纵臂焊接件各钢板的最佳厚度；

3)在纵臂折弯处采用较大的圆弧过渡，避免产生应力集中；

4)将纵臂由纵臂铸件和纵臂焊接件焊接的方式改为全焊接件焊接，材料改为屈服极限比较大的DB590材料；

5)通过参数化优化设计，将主销内倾角由原来的6°改为3°.为保证主销内倾角的度数，将原纵臂铸件所铸造的主销配合孔，用一个专门的圆柱筒来替代，该圆柱筒与其余的纵臂焊接件焊接连接.

3.2 改进后单纵臂悬架有限元模型的建立

将改进后的单纵臂悬架重新在Solidworks软件中建模，并再次导入到ABAQUS有限元分析软件中，得到改进后的悬架三维模型如图16所示.

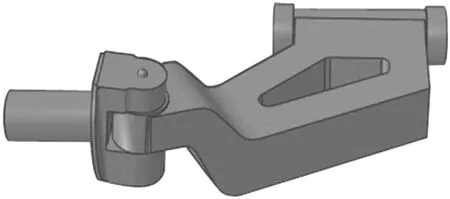
图16 改进后的单纵臂悬架三维模型示意图

3.3 材料的选择及网格的划分

改进后的纵臂钢板焊接件采用的材料是DB590，具体的参数如表2所示.同时赋予该材料的塑性特性数据.

表2 纵臂材料的选择

对于改进后的前桥模型的网格划分仍然采用手动布置种子的方法.重新划分好网格后的前桥模型如图17所示，经过网格检查高亮显示，可知网格的大小、均匀程度及数量都较好，符合计算的要求.

图17 改进后单纵臂前桥的有限元网格模型

为了便于与改进前的模型进行分析比较，同样对新建立的前桥模型进行3种工况条件下的应力和应变分析，以观察前桥纵臂在经过改进后的受力和变形情况.

3.4 改进后纵臂的弹塑性力学分析

3.4.1 满载冲击工况.

满载冲击工况是将50 t的重力在0.36 s的时间内加载到新的前桥模型的转向节臂上，其余约束保持不变.此时，纵臂所受的最高应力随时间变化的曲线如图18所示.

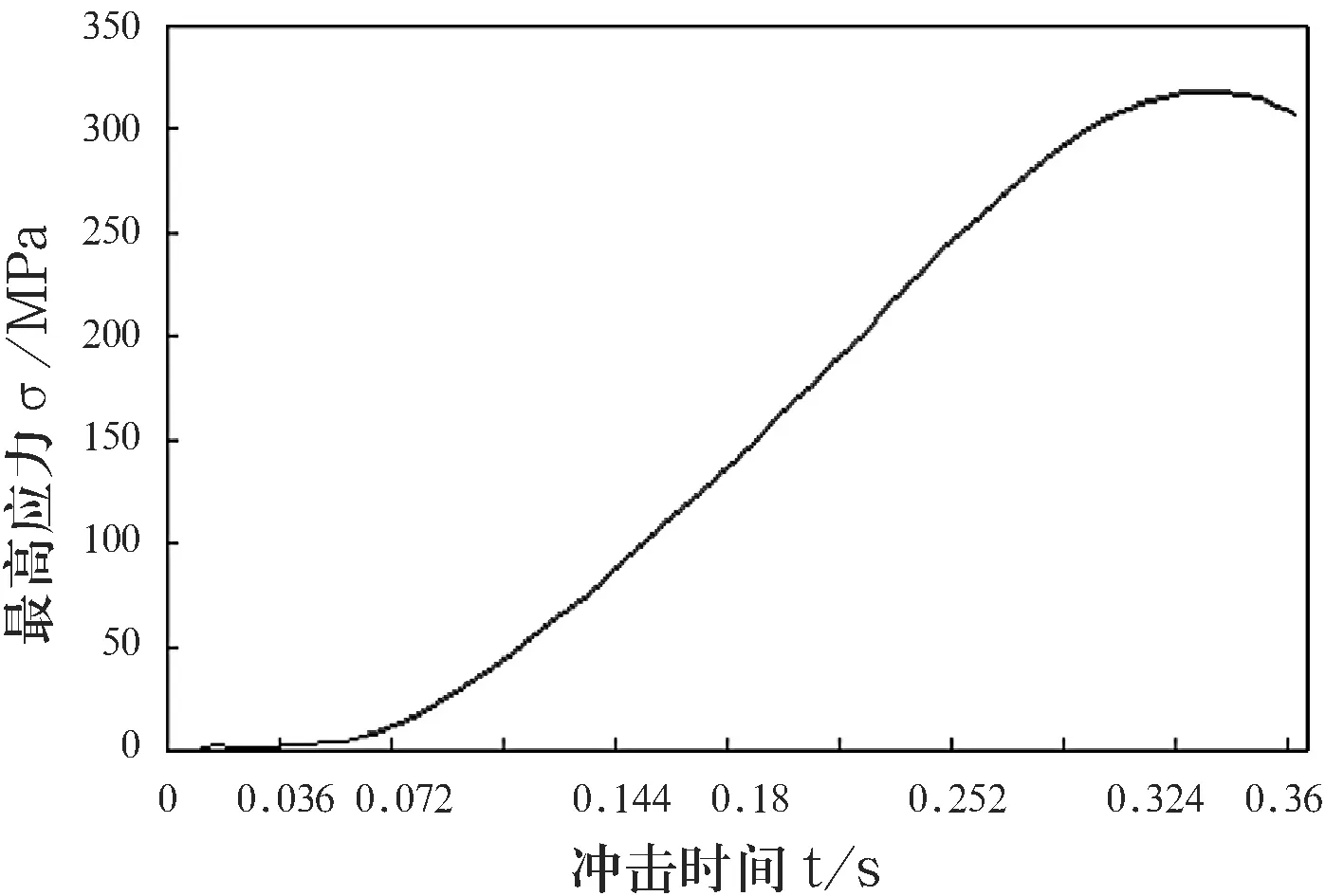
图18 改进后纵臂所受的最高应力值随时间的变化曲线

从图18可以看出，纵臂所受到的最大应力值为318 MPa，远小于DB590材料的屈服极限.纵臂所受的最高应力随时间的变化曲线光滑，过渡平稳.在冲击过程中，纵臂的塑性变形值始终为零，表明改进后的纵臂处于满载冲击工况时，材料始终处于弹性变形阶段，未发生塑性变形.

3.4.2 动态左转向至极限工况.

在车轮向左转向至最大39°的过程中，改进后的模型其动态加载过程同原模型，纵臂所受到的最高应力值随时间变化的曲线如图19所示.

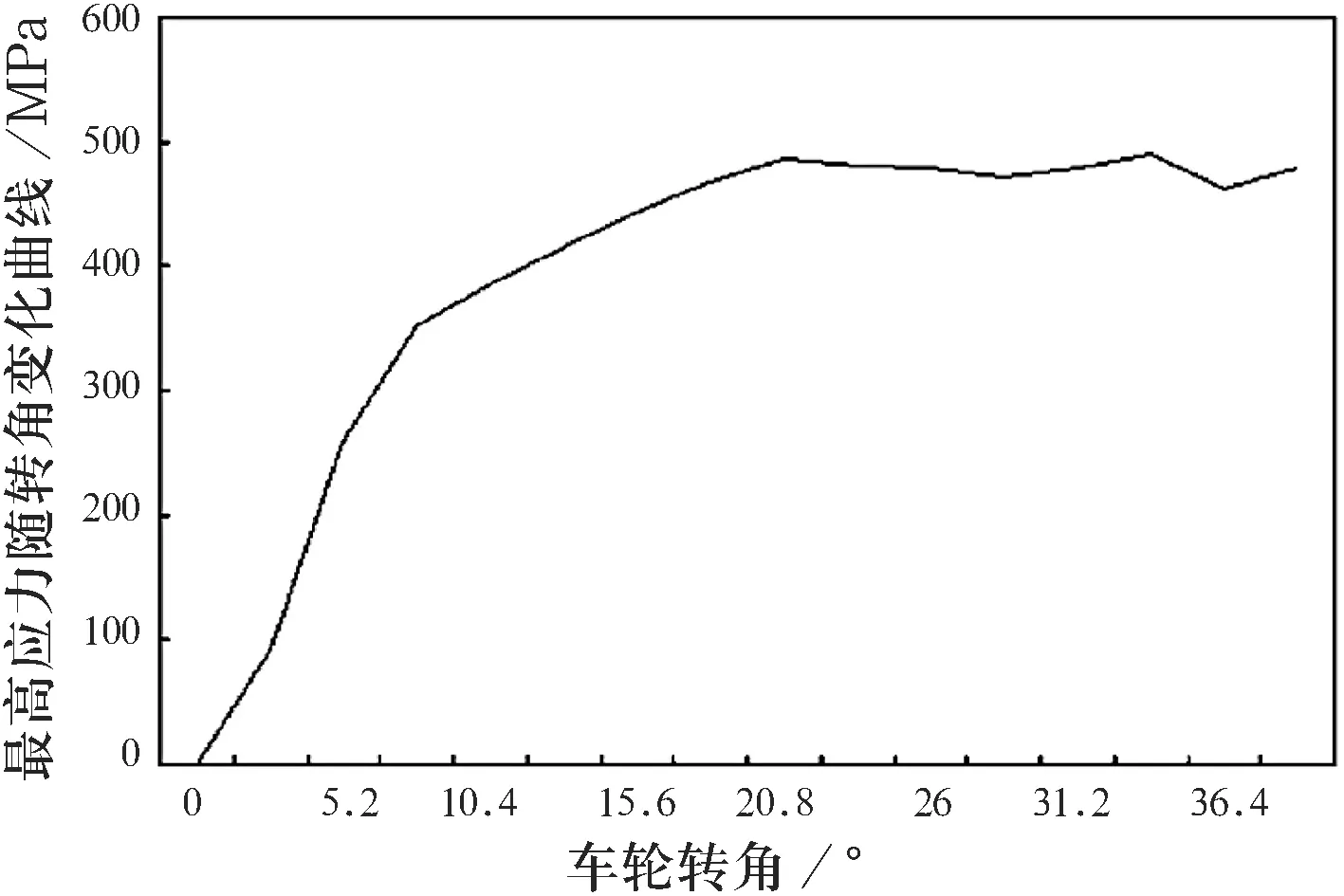
图19 左转向时，改进纵臂的最高应力随转角变化曲线

从图19可以看出，该工况最大应力值为490 MPa，小于材料DB590的屈服极限.在左转向至极限的工况中，改进后的纵臂的塑性变形值始终为零，表明改进后的纵臂在这一工况下，材料始终处于弹性变形阶段，未发生塑性变形.

3.4.3 动态右转向至极限工况.

在车轮向右转向至最大27°的过程中，改进后的模型其动态加载过程同原模型，纵臂所受到的最高应力值随时间变化的曲线如图20所示.

从图20可以看出，该工况最大应力值为464.2 MPa，小于了材料DB590的屈服极限，同时也小于左转向时的最高应力，说明该工况下不存在干涉.同时，在右转向至极限的工况中，改进后的纵臂材料的塑性变形值始终为零，这表明改进后的纵臂在转向节右转向至极限的工况下，材料始终是处于弹性变形阶段，未发生塑性变形.

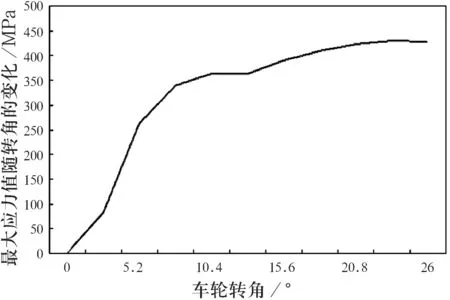
图20 右转向时，改进纵臂的最高应力随转角变化曲线

4 结 语

本研究通过对矿用汽车前桥纵臂的断口进行宏观分析和弹塑性能的有限元分析，得出如下结论：在矿用汽车前桥纵臂的结构件设计阶段，对材料的选取要保证足够的安全系数；当纵臂处于不平整路面冲击和左右瞬时转向的工况下，在纵臂与转向节相连接的上下表面、纵臂与主销的连接侧面、纵臂折弯处以及纵臂与销轴转动连接处都会出现比较大的冲击载荷，在设计时候应对这些部位重点加强，以避免应力集中；针对单纵臂悬架所出现的纵臂断裂情况，在工艺处理上给予改进，还应选用DB590这种屈服强度更大的材料，以保证材料不发生变形.同时，在生产过程中，应加强质量的过程管理，尤其是要对铸造、焊接等加工工艺进行实时监督，并在试车前对所用零部件进行严格的检测.