电液提升装置能量回收系统设计及分析

聂 波,张 进

(1.咸宁职业技术学院 工学院,湖北 咸宁 437100; 2.江苏大学 机械工程学院,江苏 镇江 212000)

提升装置的工作效率与环保节能效果密切相关,随着限制全球变暖的排放标准变得日益严格[1],提高机器能源效率已经成为备受关注的问题[2-3].提高移动机械能源效率主要有两个方面:一是提高能源的利用效率;二是实现能源的回收利用.移动机械工作中的两种主要可回收的能量形式是动能和势能[4],实现动能和势能的有效回收，使移动机械能够在原始能源的作用下运行更长时间.在移动机械领域,已经提出的能量回收形式可分为3种[5]:基于液压蓄能器的能量回收系统;基于蓄电池或超级电容器的能量回收系统;基于飞轮的能量回收系统.利用势能进行再生已经广泛应用在电梯、挖掘机、起重机和叉车中[6-7].电动液压叉车作为移动机械,具有能量转换率高、操作灵活等特点,可实现货物的叉取、升降和堆垛等操作,被广泛应用在车间、食品、仓库等对环境要求较高的作业场合.由于电动叉车的功率容量有限,初始成本高,因此，电动叉车的电能损耗尤为重要,电池的更换系统不具有时间效率[8-9].此外,提升装置的提升功能和叉车的牵引力消耗了大部分能量.在设备的其他功能方面,没有能量可回收,而且动能水平相当低,无法有效回收能源,更加迫切地关注电动叉车的能量效率[10].

学者们针对叉车负载和能量回收效率已经做了大量研究[11-13].但大多以现有液压叉车结构为基础,对于需要更高作业范围需求的叉车,需要两级提升作业,未从理论仿真和试验相结合方面,深入研究叉车的节能效率.

本文以新型电动液压叉车作为移动设备的研究对象，分析了叉车升降结构,基于叉车结构设计了能量回收系统,建立了各主要元件的数学模型,并在Matlab/Simulink中建立了能量回收仿真模型.从能量回收的角度,通过在能量回收系统中使用不同的下降速度和有效载荷,对不同提升区的节能率进行了研究,研究了不同提升区的节能效果,分析了两个不同的提升区之间的差异,以期提高叉车的能量利用率,最大限度地实现能量回收利用.

1 系统组成

1.1 叉车升降结构

为满足更高的作业范围需求,将电动叉车的提升机构设计为两级提升装置,如图1所示.分为第1提升区(自由提升区)和第2提升区,自由提升区通过一个单作用液压缸完成,第2提升区通过两个并联的单作用液压缸实现.第2提升区液压缸固定在叉车底座上,自由提升区提升装置可随第2提升区液压缸的伸缩发生相应的位置变化.

1.2 能量回收系统

为实现升降过程中能量的回收,本文设计了电液提升能量回收系统,以最大限度实现势能回收,其系统原理如图2所示.

电液提升能量回收系统主要由控制系统、供电系统、液压系统和执行系统4部分组成.控制系统主要实现对压力、高度、电流、电压信号的采集和处理.供电系统为液压系统提供驱动能量,传统液压叉车依靠铅酸蓄电池提供能量,本实验装置电能来自电网的直接转矩控制(Direct Torque Control,DTC)伺服驱动转换器,而不是蓄电池.采用一种固定开关频率的改进型DTC,控制永磁同步电机驱动器,该驱动器直接操作泵.通过改变液压泵/马达的转速实现提升系统的速度控制.

图1 新型叉车升降结构Fig.1 New lifting structure of forklift truck

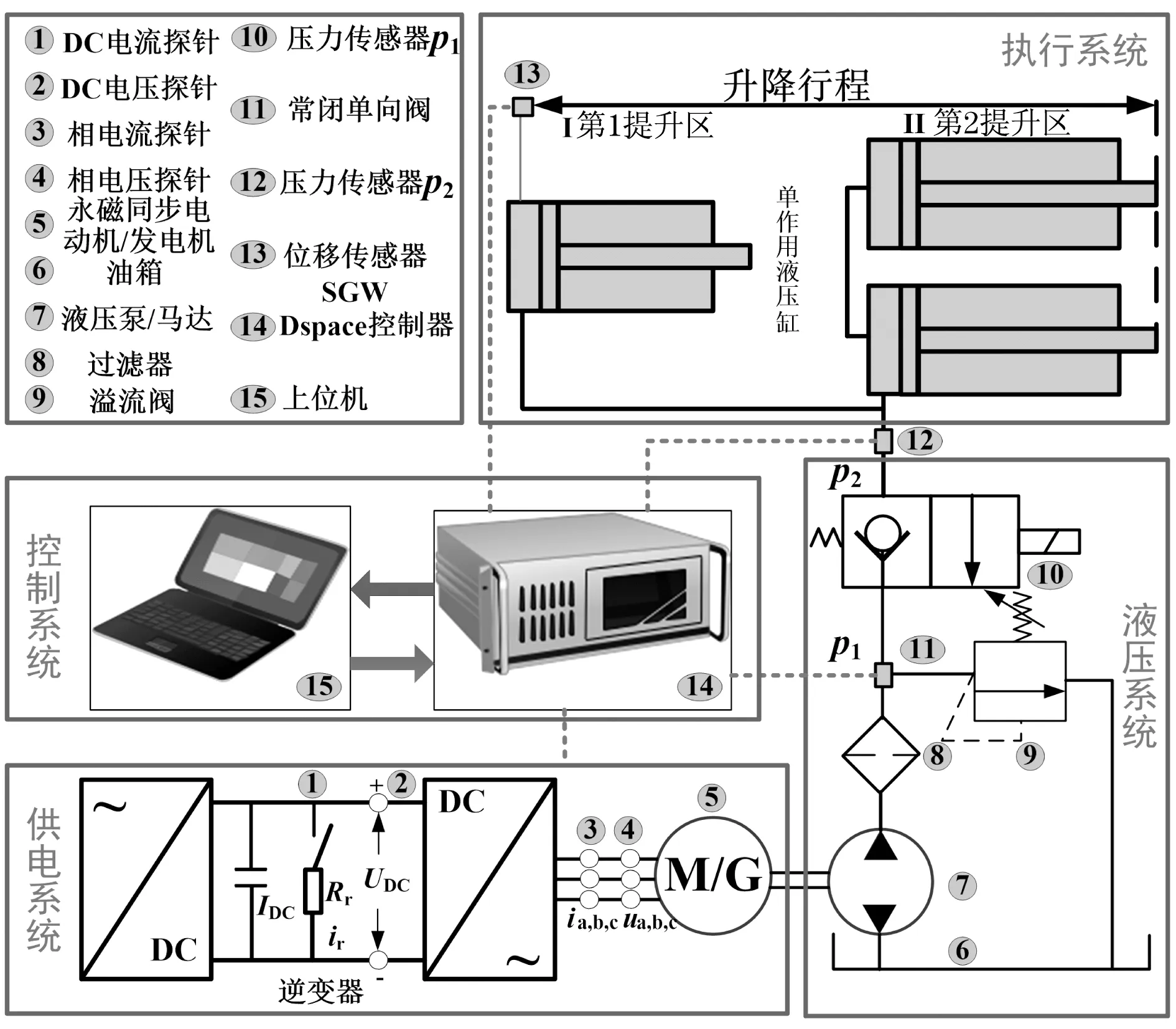
图2 电液提升能量回收系统Fig.2 Electro-hydraulic lifting energy recovery system

液压系统为执行系统提供能量,液压系统中包含的两位常闭单向阀,可防止叉车臂意外下降.执行系统包含第1液压缸和第2液压缸,液压活塞连接在两个主要的垂直桅杆上.为进一步降低能量损耗,在整个液压系统中，未使用换向阀或调速阀作用速度控制元件,直接通过调节电动机的转速实现提升区液压缸流量和速度的控制.

本研究中采用双向液压泵/马达作为能量转换元件.在提升过程中,作为液压泵元件,永磁同步电动机驱动液压泵工作,消耗能量;下降过程中,作为液压马达元件,依靠重力势能驱动马达旋转,进而带动永磁同步电动机发电,将电能储存在逆变器中,实现能量回收.永磁伺服电动机的额定效率远高于90%,具有极低的开关和导通损耗,因此，可进一步的提高能量回收率.

2 数学模型建立

电动叉车能量回收系统是一种混合系统,为了得到提升区升降过程中的能量效率和节能率,建立电动机、液压缸和液压泵的数学模型,进一步建立了能源效率和节能率模型.

2.1 电动机模型

电动机是影响叉车势能回收的主要因素之一,因此，有必要建立电动机的控制模型,提高电动机的能量转化效率.带有转子表面安装磁体的永磁同步电动机的转子可以被认为是非凸,并且假定在通过电动机中心的任何轴上都有相同的磁阻.因此,永磁同步电动机的电流向量计算公式为

(1)

式中:ia,ib,ic为瞬时相电流.

电流向量可以分解为d轴分量id和q轴分量iq.

定子d轴和q轴的绕组磁链计算公式为

式中:ψPM为永磁磁链;Lsd，Lsq为d轴和q轴磁链系数.

d轴和q轴的电压计算公式为

式中:Rs为电动机电阻;ωm为电动机角速度；ψsd为d轴绕组磁链；ψsq为q轴绕组磁链.

在额定工况下,电动机参数为Rs=0.193 Ω,Lsd=Lsq=0.31×10-3H.这些参数依赖于电动机的工作点,但电动机参数的不确定性并不是整个系统的主导因素,因此，在本仿真中这些参数是恒定的.

电动机角速度ωm与转子实际转速Ω相关,计算公式为

(6)

式中:p=3为极对数数目.

非凸极永磁同步电动机的电磁转矩公式如下:

(7)

加速度是由电磁转矩和负载转矩之间的差异以及负载与电动机的组合惯量等因素决定,其计算公式为

(8)

式中:TL为负载扭矩;Jeq=Jp+Jm为总等效转动惯量,其中,Jp=1.1×10-3kg·m2为负载组合惯量,Jm=88.2×10-4kg·m2为电动机组合惯量.

空间矢量表示通常忽略铁损耗,并且不容易将铁损耗电阻与磁化电感并联.因此,本文给出了气隙损耗的简化表达式,并利用减小的端电压计算了铁损耗，即

(9)

式中：us为磁电压；Lm为磁化电感；Lsσ为非凸极磁化电感；RFe(f)为磁化电阻.

当机器频率变化时,铁损电阻随时间的变化而变化,本文假定损耗随频率平方而变化.

2.2 液压缸模型

基于活塞运动方程和动态压力方程,建立了单作用液压缸的数学模型.根据流量连续性方程可得

(10)

式中:Be为体积模量,Be=1 400×106Pa;ps为系统压力,Pa;V=V0+xpSp为液压缸体积,m3;xp为活塞位移，m；Sp为活塞横截面积，mm2；Qin为输入流量,m3/s.其中,第1活塞横截面积为Sp1=0.002 8 m2,初始体积为V0,第2活塞横截面积为Sp2=0.002 6 m2.第1和第2活塞长度分别为Lcy1=0.88 m和1.82 m.

根据牛顿第二定律获得活塞的运动方程如下:

(11)

液压缸摩擦力方程计算公式为

(12)

式中:σ为液压缸黏性摩擦；Fcou为库伦摩擦；Fso为静态摩擦；Cs为Stribeck摩擦;对于自由提升区σ=3 000,Fcou=0.1,Fso=600,Cs=11;对于第2提升区,σ=6 000,Fcou=2,Fso=600,Cs=11.

2.3 液压泵模型

液压泵流量方程可通过如下公式获得:

(13)

式中:Q为泵输出流量,m3/s;Vth=19×10-6m3/rev为泵的理论体积排量;ηvol=0.95为体积效率,是转速和压力的函数.

泵转动的2阶微分方程可表示为

(14)

式中:Tmotor为驱动力矩;Tp,th压缩流体所需的理论力矩;Tf,p为摩擦力矩.

压缩流体的理论力矩建模如下:

(15)

式中:ps为系统压力;po为回油压力.

液压缸内的摩擦力矩计算公式如下:

Tf,p=TvΩ+sign(Ω)[Tcou+Tsoe-|Ω|/Cs]

(16)

式中:Tv为泵黏性摩擦.

对于第1液压缸,Tv=1,Tcou=0.1,Tso=300,Cs=11;对于第2液压缸,Tv=10,Tcou=0.5,Tso=300,Cs=11.

2.4 能源效率模型

叉车升降过程中能源效率η(t)与输入、输出能量相关,在时间间隔[t1,t2]内,可定义为

(17)

式中:Eout，Ein分别为[t1,t2]时间段内的总输出能量和总输入能量.

2.5 节能率模型

叉车的节能率主要与升降过程中消耗能量、回收能量相关,为了研究不同提升区效率,将节能率ηr定义为

(18)

式中:E1为无能量回收时叉车的能耗;E2为具有能量回收时叉车的能耗.

在提升系统中,叉车能量消耗计算公式分别为

式中:Em为电动机输入能量;ηinv为逆变器转换效率,假定为常数92%;Er为回收能量;ηsc为超级电容器的放电效率.

电动机输入能量Em和回收能量Er的计算公式如下:

式中:iabc，uabc为用传感器探针测量的电动机端相电流和相电压;ir，ur分别为测量的电阻段电流和电压.

因此,节能比ηr可根据下式重新计算:

(23)

3 结果分析

为了验证本文所提模型的正确性,同时研究不同因素下的节能效果,在Matlab/Simulink中建立了电动叉车提升系统的微分方程,通过对比仿真和实测结果,证明所建立模型的正确性.并进一步分析了不同下降速度和不同有效载荷下,新型电动叉车的节能效果.

3.1 模型正确性验证

在提升过程中,永磁同步电动机驱动功率为10 kW,有效载荷为800 kg,自由提升区液压缸伸出量为1.5 m,第2提升区液压缸伸出量为3.0 m.下降过程中,控制货叉速度为0.2 m/s,第2提升区和自由提升区液压缸先后复位到初始位置.获得不同提升区仿真和试验结果各参数如图3和图4所示.

图3 自由提升区仿真和试验结果Fig.3 Simulation and test results of free lifting zone

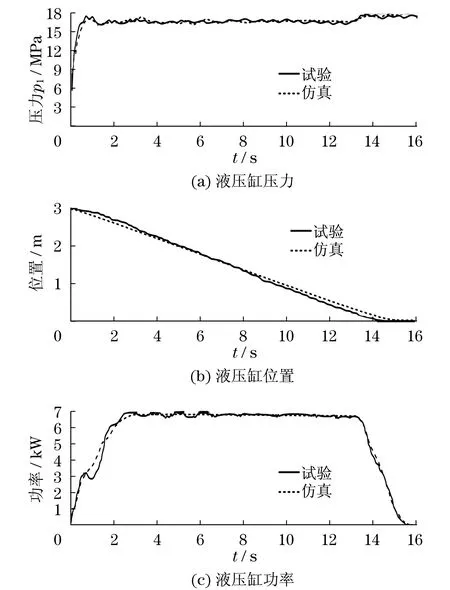
图4 第2提升区仿真和试验结果Fig.4 Simulation and test results of the second hoisting zone

由图3和图4可以看出：当第2提升区液压缸运动到最低位置和自由提升区液压缸突然启动下降运动时,会产生剧烈的振荡.在两液压缸交叉控制过程中需要更流畅的控制.基于仿真和试验结果,获得自由提升区和第2提升区各参数统计结果,如表1所示.

自由提升区、第2提升区仿真及试验结果误差均控制在5%以内,证明了所建立数学模型和仿真模型的正确性.

此外,第2提升区的势能是自由提升区的2倍,但第2提升区回收能量约为自由提升区的3倍.大部分的回收能量发生在第2提升区,自由提升区、第2提升区回收率分别为49.5%和67.2%.

表1 不同提升区仿真和试验结果对比Tab.1 Comparison of simulation and test results in different hoisting zones

3.2 节能率影响因素分析

为进一步研究不同参数下的本文所提模型的节能效果,对下降速度和有效负载下的节能率进行了研究,以期获得最佳的控制参数.

在不同速度和有效载荷下，自由提升区和第2提升区的节能率如图5所示,统计结果如表2所示.假设两提升区货物的提升和下降操作时间均为10 s,且提升总高度相同.

图5 不同速度和有效载荷下节能率Fig.5 Energy-saving rate under different speeds and effective loads

表2 不同速度和有效负载下节能率Tab.2 Energy-saving rate under different speeds and effective loads

表2中可以看出：在相同负载下,自由提升区和第2提升区节能率均随着下降速度的增加而减小.这是因为在最低转速(0.2 m/s)时,电气损耗占主导地位,发电效率降低;在最高转速(0.6 m/s)下,液压流体摩擦损失占主导地位.与电气损耗相比,液压流体摩擦损耗要远大于电气损耗,因此，其能量损失更大,导致节能率随速度的变化而降低.

在相同下降速度下,自由提升区和第2提升区节能率均随着有效载荷的增大先增大后减小,节能率并非与有效载荷呈正比关系.这是因为随着有效载荷的进一步增大,整个回收系统液压系统功率增大引起发热量增大,改变了液压系统和电气系统的参数,导致回收效率发生下降.

此外,在相同速度和有效负载下,第2提升区的节能率始终高于自由提升区,进一步说明了能量回收主要发生在第2提升区.

从表2可以看出:在自由升降区,在0 kg有效载荷下,下降过程由于负载较小,液压缸伸出量保持不变,没有油液通过液压马达,无能量回收,必须依靠外力将货叉恢复初始位置,所有的势能都转化为热能损失;在第2提升区下降阶段,液压泵/马达在所有情况下都处于马达工况下,即使有效载荷为0 kg,同样具有能量转化,其节能率相当高.

4 结语

针对传统电动叉车能源利用率低的问题,本文提出了一种适合于更高作业范围新型电动叉车.设计了叉车能量回收系统,分析了能量回收系统工作原理,推导了各元件的数学模型及节能率模型.为了证明所建立数学模型的正确性,同时研究不同因素下的节能效果,在Matlab/Simulink中建立了电动叉车提升系统的微分方程,通过对比仿真和实测结果,证明了所建立模型的正确性.分析了不同速度和有效载荷下两个不同提升区之间的节能率差异.结果表明:在自由升力区,节能率从0%～49.5%不等;在第2提升区,节能率在23.6%～67.2%之间,系统最大节能效果发生在第2提升区.通过合理调整升降速度和有效负载,可补偿液压系统的损失,说明本文所提回收方法是可行的.