基于核的分层贝叶斯断路器故障诊断方法

祝海宁,丁云飞

(1.上海电机学院 资产与实验室管理处,上海 201306; 2.上海电机学院 电气学院,上海 201306)

断路器是一种常见的广泛应用于电力系统中重要电力设备,不仅基数大,经济上的投入也很大.断路器能够根据电力运行状态进行切换或通断,其可靠性直接关系到整个电网的安全稳定性.它自身的故障状态往往会引发电力系统的较大事故,产生较大的社会和经济方面的影响.因此,针对断路器的工作状态进行准确高效的故障诊断分析,对于电力系统的安全运行以及电网质量的稳定都具有重要的意义.

故障诊断技术是通过对提取的故障数据样本建立故障诊断模型,然后通过模型对待测样本进行模式识别和分类.目前应用较多的故障诊断方法都是基于人工智能的方法.专家系统通常是通过对故障信息建立专家知识库和推理规则,或者与其他方法结合如小波分析等进行诊断[1-3].神经网络模型容易建立,在断路器的部分故障状态下仍可应用于其他单元诊断[4-5],与其他优化算法如粒子群[6]、贝叶斯决策[7]和主成分分析方法[8]相结合可提高断路器的故障诊断正确率.近来,支持向量机(Support Vector Machine,SVM)作为一种核方法广泛应用在断路器故障诊断领域,它还可以结合核主成分分析、因子分析、粒子群优化等方法来简化输入特征样本,优化算法收敛,提高分类准确率[9-11].

然而这些方法在对断路器故障进行诊断时,会存在一些难点.比如基于专家智能系统的诊断方式的难点是如何建立和更新非常依赖于专家经验的知识库,以及如何解释推理机制;将遗传算法和神经网络引入到故障诊断中可使诊断模型更加复杂,模型训练时需要尽可能多样本来提高精度,计算量也随之增大.基于SVM的算法虽然实现了非线性映射,但模型还是需要大量支持向量,随着样本增加,运算量增加也很大.

在实际运行中,断路器故障原因比较复杂.当断路器处于非正常工作状态时,断路器设备所在的回路以及设备本身会伴随着一些与故障明显相关的特征,即有关的电气量波动明显,而相关的非电气量也会发生很大变化.本文针对SF6气体断路器,通过一种基于核的分层贝叶斯故障诊断方法提取分析相关电气量以及非电气量信息,从而能使断路器故障时快速报警和诊断,并降低误报的频次,尽可能保证电网的安全可靠供电.

1 基础理论

1.1 核主成分分析(KPCA)

KPCA是一种核方法,是主成分分析(Principal Component Analysis,PCA)的一种延伸.首先,定义一个样本空间X及其在高维空间的映射φ(X)为

然后定义一个核函数K,对于任意xi,xj∈X都有如下等式成立:

(1)

目前，应用较多的核函数有多项式核、高斯核、Sigmoid核、B样条核等.KPCA先将样本输入空间里的X转换到高维向量空间;然后对高维空间中线性可分的映射样本进行PCA,提取主要成分对应的特征向量;再对原样本集进行特征提取和降维处理.用C表示高维空间的协方差矩阵,则有

(2)

其特征值λ和特征向量v需要满足:

(3)

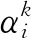
式(3)通过点积可以变为

(4)

由式(4)可推出

(5)

根据式(1)的定义,式(5)可以简化为

(6)

对式(6)求解就可以得到λ和v.而特征向量在高维空间的映射变为

(7)

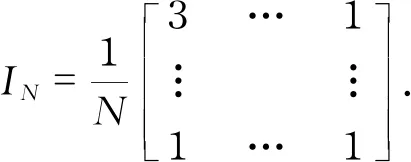
KPCA还需要对高维空间进行预处理,则核矩阵可以通过下式完成中心化：

(8)

1.2 分层贝叶斯模型

分层贝叶斯模型是基于贝叶斯概率分析的一种监督学习方法[12].通过对两层先验参数的分布进行设定,能令模型中的部分参数系数减少到0,根据需求调节模型的复杂度,提高运行时间.给定N个数据的一个输入训练集合D={(x1,y1),(x2,y2),…,(xN,yN)},这里xi∈(1,2，…,N)为D维输入向量,yi∈(1,2,…,N)为一个二值输出向量.给定N×M维矩阵H=[h(x1),h(x2),…,h(xN)]T,M为所选基函数个数.于是可以得到含有潜变量z的模型

(9)

式中:z=(z1,z2,…,zN)T;w为符合高斯分布的零均值的单位误差向量,可以表示为p(w)=φ(w|0,1);β为需要估计的参数.

模型根据z≥0时y=1,以及z<0时y=0来进行分类,即满足

(10)

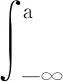
对z求取似然函数如下:

(11)

为了便于对β求取参数的估计值,令βi满足

(12)

模型中z和新引入的τ=[τ1,τ2,…,τM]T都是未知数据,这里将模型分层能够容易通过期望极大(Expectation Maximization algorithm,EM)方法实现对参数的估计.将Jeffreys分布引入到τ上能够减少额外参数参与到运算中[13],从而简化参数估计模型.由式(11)、式(12)能够得出

(13)

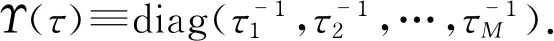
通过EM算法,求出对Υ的期望值V和z的期望值s,这里t是迭代次数,从而得出

(14)

(15)

联立式(13)～式(15),可以求得参数β为

(16)

为了避免迭代过程中除以零的出现,新定义一矩阵

(17)

则式(16)可以变为

(18)

2 故障诊断方法

本文所提出的故障诊断方法,首先采用KPCA对原数据进行特征值提取,从而找出训练样本在高维映射中的特征向量.其次,将核方法引入分层贝叶斯模型中，这里的核函数都选择相同的高斯核函数.同时,由于该分层贝叶斯分类器只能解决两类分类问题,而生产过程中出现的故障往往是多于两类的.本文采用故障树中的二叉树理论,建立一系列对应不同故障类别的二分类器,进行组合诊断.整体故障诊断如图1所示.

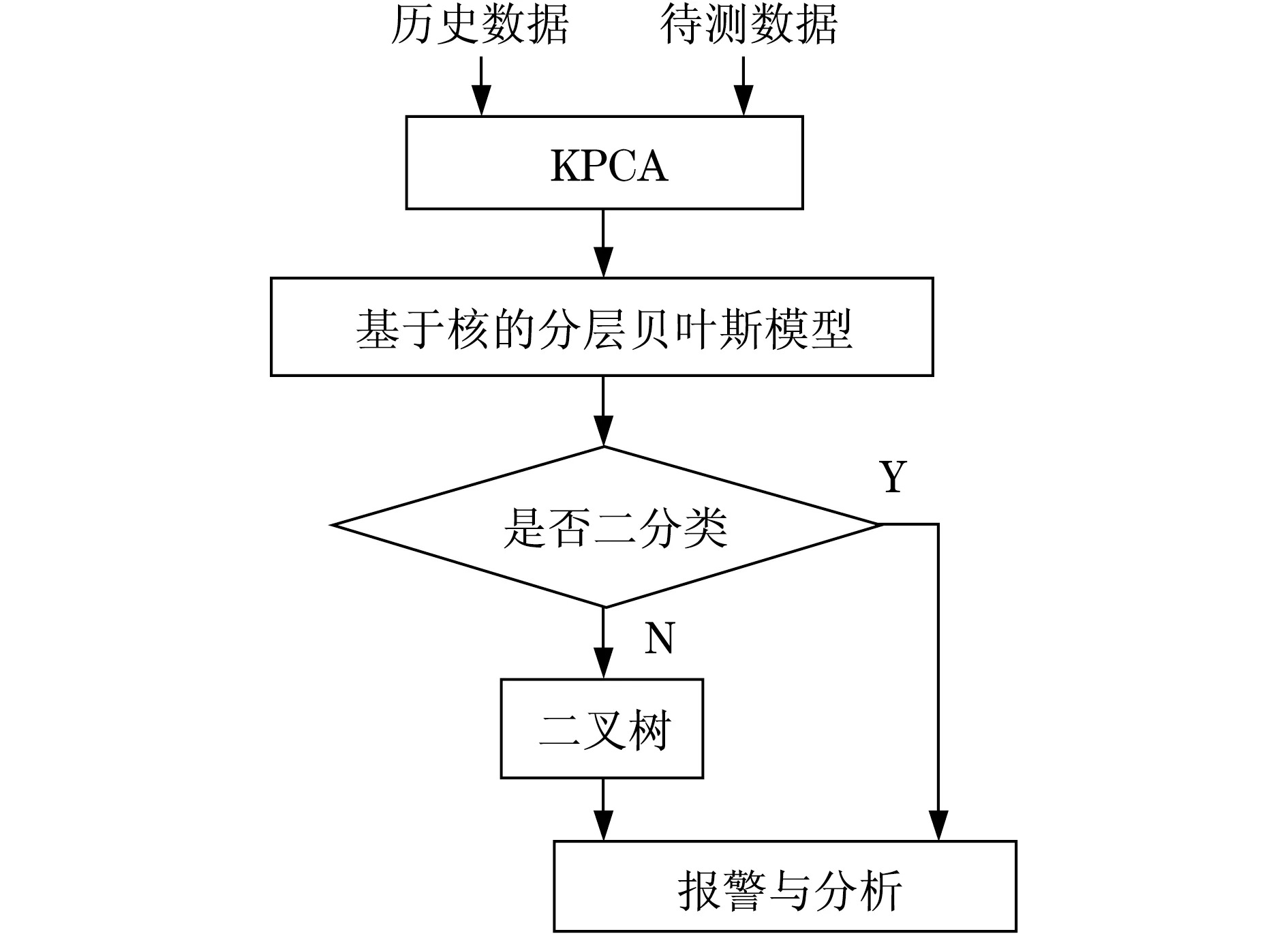
图1 基于核的分层贝叶斯故障诊断框图Fig.1 Kernel based hierarchical Bayesian framework for fault diagnosis

具体的故障诊断算法步骤如下:

步骤1对历史训练数据和待测数据标准化,并对模型参数进行初始化和设定迭代终止条件.

步骤2利用高斯核函数如下所示,计算核矩阵K,即

(19)

式中:δ为核宽参数,可以由交叉寻优方法来确定.

步骤3按照式(8)修正核矩阵得到K′.

步骤4根据系统要求,按照式(7)计算特征向量的投影tk,从而得到映射后的训练数据集X.

步骤5利用核方法对X重新定义，并求取设计矩阵,于是H中的向量变为

(20)

步骤6将H代入到分层贝叶斯模型中,通过式(15)和式(17)分别求得s(t)和Q(t)值.

步骤7利用式(18)求得新的参数向量β(t+1).

步骤8重复步骤6和7,直到满足算法终止条件.

步骤9对待测样本进行分类诊断.

步骤10判断故障类别数c是否等于2.如果是,则输出诊断结果;如果不是,则采用二叉树的方法构建多类分类器:首先将故障种类中最经常发生的故障作为第一类,将其他(c-1)类故障看作另一类,重复步骤5～9,建立第1个二分类模型;然后在(c-1)类故障中重复前面的分类,建立第2个二分类模型,直到得到(c-1)个二分类器.待测样本通过这些分类器得到最后的多分类故障.

3 实验分析

实验以某电气公司3AP1FG型SF6气体断路器在线监测系统进行数据的采集.该系统包括传感器(如压力传感器PMR300和温度传感器PT100等)、数据处理系统、通讯网络(RS485总线)和监控主机.监控主机通过提取分析大量断路器故障或非正常工作时相关电气量以及非电气量历史信息,利用所提出的故障诊断方法在Matlab上对其进行离线训练;然后使用训练好的故障诊断模型对断路器故障进行在线分析,快速诊断出结果,判断属于哪类故障,并在人机界面上直观展示出来.

高压断路器SF6的故障诊断主要依赖于对采集数据的分析.实验选取能够为SF6气体断路器故障诊断提供重要的参考信息的8个非电气量，包括SF6气体微水量、SF6气体密度、导电接触部分温度、绝缘电阻、接触电阻、分合闸线圈电流、线圈电压、分合闸时间.这里主要考虑SF6断路器的常见的4种故障，包括气体泄漏、机械卡涩、绝缘闪络和二次回路故障.为验证所提出的故障诊断算法的有效性,选取故障实验训练样本400个,其中每种故障样本为100个.另外取100个样本作为待测数据集,其中每种故障样本为25个.训练样本标准化后通过核主元分析其样本阈值对主元数据样本的关系如图2所示.从图2中曲线可以看出：KPCA对原训练样本的缩减效率，当阈值增加时,缩减的数据组数则减少,也就是说为了达到某一阈值所需要的样本数量增加了；关系图的斜率在阈值取0.96～0.98时最大,此时在此阈值区间内对应的缩减样本所含原信息量在保持一定的缩减成本之下是最大的,即核主元转换效率最高.所以最优的阈值设为0.97,对应的新的样本数为280组.

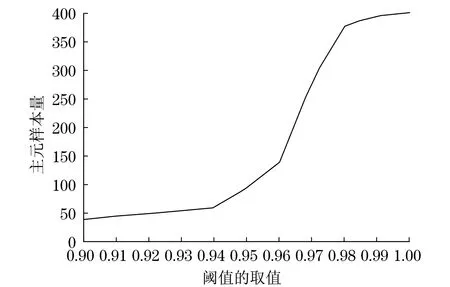
图2 KPCA阈值与主元样本量关系图Fig.2 The relationship KPCA between threshhold and remained samples

将新训练样本通过二叉树训练出3个基于核的分层贝叶斯模型,然后将100个测试数据分类.在相同的初始条件下,该方法与其他另外两种广泛应用的方法进行了比较.① KPCA通过统计方法求取T2和平方预测误差(Squared Prediction Error,SPE)统计量,判断样本的显著误差,从而进行故障诊断.② 将SVM和二叉树结合实现的断路器的多类故障诊断.其分类结果如表1所示.

表1 故障诊断结果Tab.1 The result of fault diagnosis

表1中:F1～F4表示4类故障中每类故障所对应的错分样本数目;正确率是针对整个测试样本的正确分类的准确率;nsv表示3个二分类模型需要的支持向量的平均个数.从表1中可以看出：分层贝叶斯的分类准确率比其他两个方法都高些,KPCA较低,并且它是基于统计的方法来判断故障类别,所以没有具体的支持向量个数.然而对于SVM而言,它的平均nsv为42个,但分层贝叶斯只需要19个.这说明在分类精度相差不大,甚至更好的情况下,后者所建立的模型参数个数比前者少一半左右,模型的结构要更为简单,计算效率相应更高.

4 结语

本文针对电力系统中常见的断路器设备的故障,提出了一种基于核的分层贝叶斯故障诊断方法.该方法利用断路器的8个故障特性参数为输入样本,利用KPCA对原故障训练集合进行缩减,并最大限度地保留原始数据集的信息.然后在新数据样本的基础上，训练已经利用核方法改进的分层贝叶斯模型.这样就可以通过核函数隐式映射为高维线性关系,实现非线性故障诊断.根据故障类别数,结合二叉树进行多类故障诊断.通过实例分析,该故障诊断方法与另外两种方法KPCA和SVM的故障诊断结果比较表明,所提出的基于核的分层贝叶斯故障诊断方法在数据样本缩减、模型参数简化、分类准确率上都好于另外两种方法,从而验证了本文方法的有效性.