基于低能耗的铣削参数优化
邓 伟,罗 毅,罗金刚
(贵阳学院 机械工程学院,贵州 贵阳 550005)
能源问题一直是国际关注的重点问题,相关研究报告显示全球近1/3的能耗来源于制造业[1].中国工业领域的能源消耗约占中国能源消耗总量的71%,其中制造业的能源消耗约占整个工业领域能源消耗的81%[2].机床作为制造业中的主要加工设备,机加工过程的切削参数选择不仅影响到加工成本、质量及加工效率,还会影响到机加工过程的能量消耗.
针对铣削过程中的能耗及参数优化问题,国内外学者做了大量的研究.Rodrigues等[3]提出考虑切削速度和刀具切削角度影响的机床比能耗模型,并分析了切削速度和刀具角度对能耗以及粗糙度的影响规律.Bhushan[4]主要针对特定的加工铝合金SiC颗粒复合材料的过程,以最低能耗和刀具最大寿命为优化目标,并在数控机床上进行了实验验证.Mativenga等[5]以能耗最小目标对切削三要素进行优化,揭示了如何通过减小能源密度和能源成本来降低碳排放,并利用最小能耗准则,显著地降低了机加工过程中成本、能耗和碳排放.Hanafi等[6]以最低功耗和最优表面质量为优化目标,基于灰色关联和田口优化方法进行了切削参数优化,得出了切削速度和切削深度是最具影响力的因素.张楚锋等[7]以能耗和成本作为优化目标函数,采用回归分析法获取铣削力参数,最后利用遗传算法对参数模型进行优化求解.李爱平等[8]以平面端铣削粗、精加工过程为研究对象,构建铣床粗、精加工总能耗模型及总生产率模型,并采用遗传算法进行参数优化,结果显示优化后的参数使得粗、精加工总能耗下降了15.04%.
切削加工中,在许用范围内选用较大的切削参数,能显著地提高切削效率,减少切削时间,但较大的切削参数也意味着较高的切削功率.若切削参数值取用较小,则切削功率降低,此时所需切削时间较长.上述两种情况都可能会造成实际切削能耗的增大.本文以铣削加工为研究对象,以实际加工条件作为约束,建立了以能耗和铣削时间为目标的多目标优化模型,采用粒子群算法对多目标优化模型求解,得到了在一定条件下的全局最优铣削参数.
1 多目标优化问题
1.1 多目标优化问题描述
多目标优化问题又称多属性、多准则、多指标优化问题.由于多个待优化目标间存在无法比较和冲突的现象,优化其中的一个目标可能导致其他目标变差,即无法使得所有的目标函数同时达到最大(或最小),这使得多目标优化问题的解并不唯一,而是一组对于各优化目标的性能指标都比较满意的Pareto最优解的集合.多目标优化的核心就是协调各目标函数之间的关系,找出使各目标函数能尽量达到比较大(或比较小)的最优解集.
若某问题有m个待优化目标,每个目标有n个优化变量,则该多目标优化问题可表述为
(1)
式中:f(x)=[f1(x),f2(x),…,fm(x)]为m个目标函数集合;gi(x)≤0为约束条件;x=(x1,x2,…,xn)为n个优化变量的集合.
1.2 前决策优化方法
根据决策方式的不同,多目标优化方法主要分为前决策法和后决策法.前决策法是在优化搜索之前给出决策信息,加权法是其中最具代表性的方法之一.通过对子目标赋予不同的权重值,将多目标优化问题转化为单目标问题求解,但在权重的选取上,由于多带有主观偏好,权重的选取将会直接影响到后面的优化结果.前决策法表述如下:
(2)
式中:wi为第i个目标的权重.
2 铣削过程多目标优化模型的建立
2.1 铣削约束条件
实际加工中,铣削参数的选取往往受到铣削条件的约束,主要包括铣削功率约束、铣削力约束及铣削参数约束.
铣削功率约束指铣削过程中的铣削功率不能超过机床主轴的额定功率,即
(3)
式中:Fc为实际铣削力;vc为铣削速度,m/min;ηp为铣床效率;Pmax为主轴额定功率,kW.
铣削力约束指在铣削过程中所产生的力不能超过主轴的所允许的最大铣削力,否则会导致工艺系统的破坏,降低工件质量,即
(4)
式中:ηc为安全系数;Fc,max为最大铣削力.
铣削参数约束指在铣削加工中的主轴转速n(r/min)、进给速度vf(mm/min)、铣削宽度ae(mm)及铣削深度ap(mm)不超过铣床的许用范围,即
(5)
式中:d为刀具直径,mm.
2.2 多目标函数构建
2.2.1铣削时间函数
工件铣削过程的总时间T主要包括:待机时间tf、空走刀时间tair和实际铣削时间tc,实际铣削时间tc和铣削过程总时间T计算如下:
式中:V为工件待铣削部分材料的体积,mm3.
2.2.2铣削能耗模型
根据机床在机加工过程中的工作状态,可将机加工过程的能耗分为固定能耗Ef、空载能耗Eair和实际切削能耗Ec.在铣削过程中,机床的照明系统、冷却风扇、润滑系统等处于工作状态,机床的加工状态对这部分能耗几乎没有影响,其功率的大小只与本身的特性有关,决定这部分能耗大小的只有这部分功能单元的工作时间.文献[9]表明,空载功率和主轴转速满足一定的比例关系,即
(8)
式中:系数A,B,C可根据实测数据拟合得到.
空载能耗为
(9)
铣削过程的能耗为
(10)
铣削力Fc为[10]
(11)
式中:af,Z分别为每齿进给量(mm/Z)和铣刀齿数;KFc为加工不同材料时的修正系数;ke,kf,kp,kd为各参数对铣削力的影响程度系数.
2.2.3多目标函数构建
时间与能耗的量纲不同,在构建多目标优化函数时,需先对其进行归一化处理,再采用上文所提到的先决策法将铣削能耗和铣削时间赋予不同的权重转化为单目标函数.时间与能耗均属于成本型指标,多目标函数构建为
(12)
式中:λ1,λ2∈(0,1),且λ1+λ2=1,分别为时间与能耗加权系数;Tmin,Emin分别为单目标优化时的最优值.
3 粒子群优化算法
粒子群优化算法[11](Particle Swarm Optimization,PSO)基于种群中的个体对信息的共享机制,使整个群体在问题决策空间中产生从无规则到有规则的进化过程.在迭代过程中,群体里的每个粒子同时跟踪自己的历史最优值与群体历史最优值来更新自己的位置和速度,当达到迭代终止条件时,群体最优值即为所求问题的最优解:
(13)
式中:xid为第i个粒子在D维空间的位置;vid为对应速度;pid为第i个粒子的最优值;gid为整个群体的历史最优值;k为迭代次数;w为惯性权重;c1,c2为对自身和对环境的学习因子;rand1和rand2为[0,1]之间的随机数;ε为速度约束因子.算法详细步骤见文献[12].
4 优化实例
待铣削工件材料为HT250,铣刀为4刃硬质合金刀具,刀具直径d=20 mm,待加工特征为60 mm×60 mm的平面,加工余量取0.5 mm.铣床主轴最大转速nmax=3 000 r/min,根据文献[9]所述方法,测量得到机床的待机功率为518.73 W.测量并拟合得到铣床空载功率为
(14)
取目标函数的加权系数λ1=λ2=0.5,为了简化优化过程,取ap=0.5 mm,待机时间tf=10 s,空走刀时间tair=10 s.初始化粒子群粒子数N=20,最大迭代次数K=50,速度约束因子ε=1,学习因子c1=c2=2,惯性权重w=0.8,取主轴转速300 r/min≤n≤2 500 r/min,进给速度300 mm/min≤vf≤1 000 mm/min,铣削宽度8 mm≤ae≤16 mm.铣削力计算公式(11)中的相关参数选取如表1所示.

表1 铣削力参数[10]Tab.1 Milling force parameters
当以时间为优化目标时,根据优化结果,实测时间T=36.94 s,能耗为E=39 373.31 J.以能耗为优化目标时,根据优化结果,实测能耗E=35 776.07 J,时间为T=43.61 s.以时间和能耗同时作为优化目标,优化结果如表2所示.

表2 优化结果Tab.2 Optimization results
优化结果对比如表3所示.由表3可知:在该铣削过程中,若以铣削时间较少为目标,则能耗值相对较大.以能耗最低为目标,则铣削时间相对较长.当同时考虑时间和能耗时,结果介于两者之间.当所考虑的目标重点不同时,所选择的铣削参数也不相同,选择较为合理的铣削参数对铣削过程中的节能优化有着重要的影响.
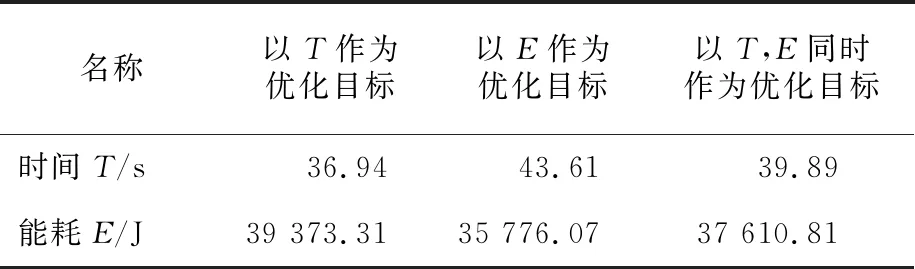
表3 优化结果对比Tab.3 Comparison of optimization results
5 结语
本文就如何使铣削时间和铣削过程中的能耗在约束条件下达到Pareto最优为目的,将铣削过程的能耗分为待机能耗、空载能耗和实际铣削能耗,建立了以铣削时间和铣削能耗为目标的多目标优化模型,以主轴转速、进给量、铣削宽度为优化变量,并采用前决策法将多目标优化函数转化为单目标函数,用PSO对该模型进行了求解,得到全局最优变量,为铣削加工的节能优化研究起到了一定的理论指导.但在实际机加工中,一个零件往往需要经过铣削、磨削、钻削等多工步或多工序,在接下来的研究中,多工序或多工步的研究将会是重点,以便为工艺路线节能优化打好基础.

