基于博弈论滤波的无人机目标跟踪
苑瑞林,朱志甫,孙 华
(1.鹤壁职业技术学院 电子信息工程学院,河南 鹤壁 458030; 2.东华理工大学 江西省新能源技术研究中心,江西 南昌 330013)
无人机已经被广泛应用于军事、航空、医学救援、远程测量等多个领域,目前,雷达/红外跟踪系统由于具有灵活性、冗余性、简单性和可靠性而被广泛使用[1-2].雷达是一种有源传感器,它利用无线电波确定目标的距离和方位角.然而,电磁信号很容易受干扰,这些不想要的信号可能来自内部和外部源,包括被动的和主动的[3].红外传感器是一种无源传感器,对电磁干扰无影响,对大气环境敏感[4],利用雷达和红外传感器可以大大提高目标跟踪精度.然而,雷达和红外传感器的测量都是非线性的,因此,雷达/红外无人机跟踪系统需要研究无人机跟踪滤波器.
模型不确定性、测量噪声和目标未知的转向指令是无人机跟踪系统中具有挑战性的问题[5-6].在文献[7]中,用一种蚁群估计器追踪机动目标.在文献[8]中,目标跟踪问题被公式化为零和博弈,并且开发了一个极大极小值算法估计目标在传感器网络中的位置.在文献[9]中,将目标跟踪问题描述为随机对策,对线性连续时间系统的h∞最优状态估计滤波器问题进行了求解.在文献[10]中,为解决无人机跟踪过程采用粒子滤波算法存在粒子贫化现象,提出了基于蝙蝠回声频率和响度变换定位机制的群智能启发算法.为了扩展线性离散动态系统约束状态变量的极大滤波器,在文献[11]中,提出了一种约束状态估计滤波器.所有的算法都假设测量矩阵是常数,它们不能用于雷达/红外目标跟踪系统中.为了解决这一缺陷,本文采用离散时间博弈理论.
首先将目标跟踪问题转化为离散时间零和对策;然后提出了一种基于博弈的状态估计算法,用于雷达/红外目标跟踪系统的同步更新算法.利用代数方法建立了该问题的求解方法,并在三维笛卡尔坐标系中开发了一种精确估计无人机位置和速度的迭代算法.该算法是一种鲁棒的极大极小值迭代滤波器,通过最差的转向命令、最小化估计误差而获得.
1 无人机跟踪模型建立
1.1 无人机运动模型
为了实现对无人机位置的精确估计,首先建立无人机的运动学模型,建立离散时间无人机动态模型如下:
(1)
式中:k为时间指数;xk∈Rn为三维笛卡尔坐标中系统在第k步的位置、速度和加速度状态向量,R为维度;C为将系统状态和无人机目标转向指令相关联的系数矩阵;zk∈Rr为测量向量;vk∈Rm和ωk∈Rr分别为过程噪声和零均值高斯序列的测量噪声,相应的协方差矩阵分别为Qk和Rk;A为状态转移矩阵;B为系统噪声系数矩阵;μk为未知转向指令向量;f(·)为非线性函数的测量模型,并在稍后定义.
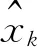
1.2 传感器量测模型
式(1)中,f(·)取决于传感器的类型.本文采用雷达/红外传感器组合形式对无人机运动进行跟踪,其量测包括目标距离、方位角及俯仰角信息.用于量测机器人位置的雷达/红外传感器设置于同一平台上,假定两个传感器位于同一位置.建立三维笛卡尔坐标下无人机与传感器平台的几何关系,如图1所示.
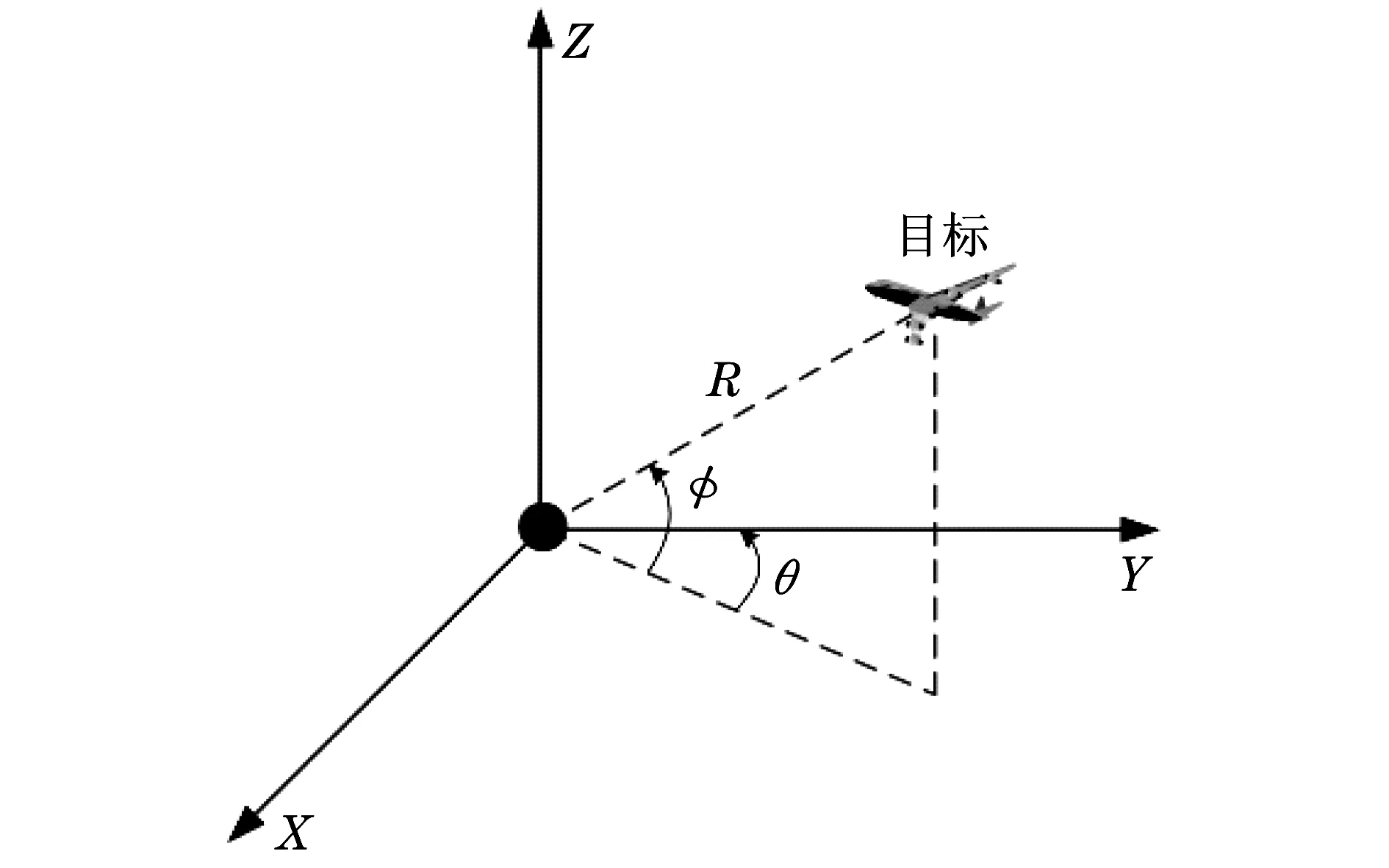
图1 无人机与传感器平台的几何关系Fig.1 Geometric relationship between unmanned aerial vehicle and sensor platform
(6)

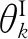
(7)
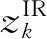
考虑到以上所述,f(xk)可写为
(8)
1.3 状态估计方法
状态估计指对无人机过去的运动状态加以平滑,并对现在的运动状态进行滤波以预测未来的运动状态.由于在目标跟踪系统中,偏状态估计滤波器比有偏状态估计更适合.采用无偏滤波器对运动状态进行估计,其滤波器结构具有零值平均初始条件,即
(9)

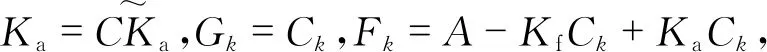
(10)

为了采用博弈论进行状态估计,将式(10)给出的估计误差分解如下:
(11)

(12)
式中:Ke为设计常数.
2 博弈论滤波算法
在获得无人机位置信息后,引入博弈论的方法对估计位置进行平滑,以提高位置估计精度,并实现目标跟踪.
2.1 离散零和动态博弈
在零和博弈中,采用离散时间动态博弈.定义成本函数为
(13)
式中:Wk为正定矩阵;N为时间范围.
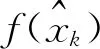
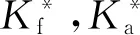
(14)
2.2 博弈解与状态估计滤波器
式中:M为协方差权重矩阵;D为对角权重矩阵.
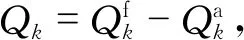
(17)

(18)
式中:Pk为协方差矩阵.
进一步,假定给出了f(xk)的雅可比矩阵Ck,则可以递归地利用以下关系得到状态估计:
电动汽车市场是我国最重要的新兴产业之一,是交通行业发展的必然结果。目前中国电动汽车市场处于萌芽阶段,朝气蓬勃,具有较大的潜力,同时具有较高的风险。但是只要采用了符合市场、符合消费者偏好的商业模式,会大大降低电动汽车行业的风险。
(19)
为获得Ck,使用式(6)和式(7)的雅可比矩阵可获得相应测量矩阵为
(20)
综合式(19)和式(20),获得矩阵Ck表达式为
(21)
可以看出Ck=Jf是一个时变矩阵.
3 仿真结果分析
为验证基于博弈论滤波的雷达/红外定位方法对无人机位置的跟踪效果,在Matlab/Simulink环境下,对无人机变高度飞行和恒定高度飞行进行了跟踪误差仿真.
3.1 仿真设置
雷达/红外传感器均位于笛卡尔坐标的原点,采样速率为t=1 s,雷达传感器的测量噪声向量是标准偏差为30 m、方位角为0.86°的零均值高斯序列,红外传感器测量噪声向量是方位角和仰角均为0.57°的标准偏差,过程噪声为0.08 m/s2的零均值高斯序列.通过100次蒙特卡洛进行仿真测量,采用均方根误差(Root Mean Square Error,RMSE)和累积均方根误差(Cumulative Root Mean Square Error,CRMSE)作为位置和速度估计的性能指标,其表达式如下:
(22)
(23)
式中:K为采样点数;T为采样时间.
3.2 变高度飞行跟踪
3.2.1标称噪声干扰
假设无人机的初始位置为[3 600 3 600 0],其运动轨迹为1~10 s,以[-10 10 20]m/s的速度做匀速直线运动;在10~25 s之间以恒定速度[20 20 20]运动;在25~40 s之间的恒定加速度[2 -2 0]运动,其后在50~60 s之间的保持速度不变.
根据无人机运动轨迹,对比博弈论滤波、扩展卡尔曼滤波和容积卡尔曼滤波下,无人机位置和速度的均方根误差,如图2所示.
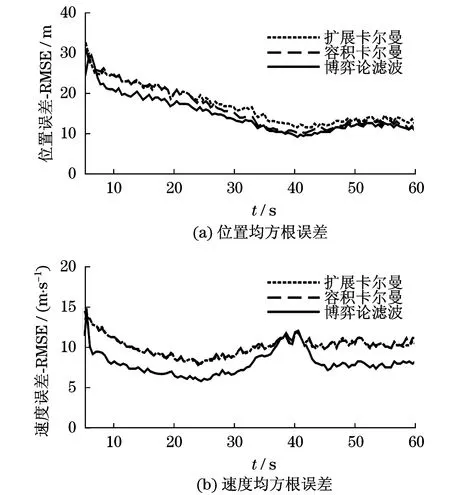
图2 标称噪声干扰下无人机变高度飞行跟踪误差Fig.2 Tracking error of unmanned acerial vehicle at variable height under nominal noise
由表1可以看出:虽然博弈论滤波能够获得无人机更准确的估计结果,但结果表明,所有滤波器均能以合理的精度估计三维笛卡尔坐标系中无人机的位置和速度.3种滤波器下的位置均方根误差分别为20.85,22.63和23.42 m,速度均方根误差分别为8.6,11.6和11.7 m/s.
3种滤波器下无人机CRMSE和运行时间如表1所示.可以看出,对比累积位置误差,博弈论滤波的比扩展卡尔曼滤波降低了6%,比容积卡尔曼滤波降低了3%.此外,博弈论滤波的累积速度误差比另外2种滤波方法减小了9%.3种滤波方法中容积卡尔曼滤波运行时间最长.

表1 标称噪声干扰下无人机变高度CRMSE及运行时间Tab.1 CRMSE and running time of unmanned acerial vehicle at variable height under nominal noise
3.2.2非标称噪声干扰
为进一步研究噪声干扰对跟踪精度的影响,采用相同的飞行路径,设置雷达传感器的测量噪声向量是标准偏差为60 m、方位角为1.72°的零均值高斯序列.红外传感器测量噪声向量是方位角和仰角均为1.15°的标准偏差的零均值高斯序列.获得无人机位置和速度的均方根误差,如图3所示.

图3 非标称噪声干扰下无人机变高度飞行跟踪误差Fig.3 Tracking error of unmanned acerial vehicle at variable height under non-nominal noise interference
从图3可以看出:3种滤波方式下位置均方根误差分别为25.63,40.71和43.65 m,速度均方根误差分别为16.36,32.64和32.85 m/s,表明博弈论滤波在非标称噪声扰动下的跟踪性能同样优与另外两种滤波方式.进一步对比分析3种滤波器的累积均方根误差,如表2所示.
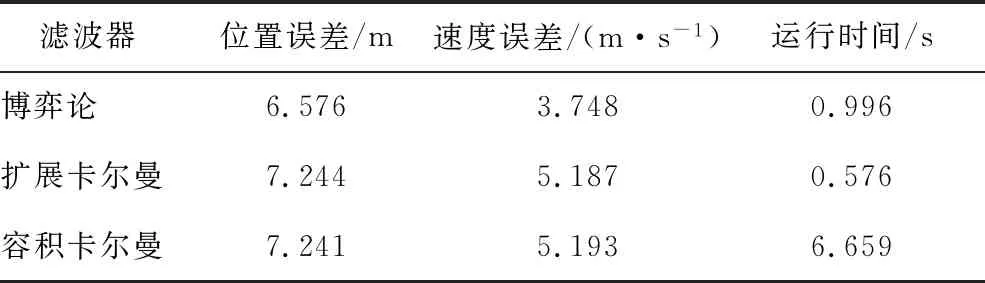
表2 非标称噪声干扰下无人机变高度CRMSE及运行时间Tab.2 CRMSE and running time of unmanned acerial vehicle at variable height under non-nominal noise
由表2可以看出:与扩展卡尔曼滤波和容积卡尔曼滤波相比,本文提出的博弈论滤波的位置CRMSE减少了12%,速度CRMSE减少了36%.
基于上述分析可知,当噪声统计量是标称时,扩展卡尔曼滤波、容积卡尔曼滤波和博弈论滤波均能以合理的精度在三维笛卡尔坐标系中估算无人机的位置、速度.但是,如果噪声统计信息未知,则本文提出的博弈论滤波具有更好的跟踪效果.
3.3 恒定高度飞行跟踪
根据无人机的特征,很长一段时间内在恒定高度飞行,因此,有必要研究恒定高度飞行下的跟踪效果.设定无人机的飞行轨迹为
(24)
3.3.1标称噪声干扰
无人机恒定高度飞行过程中,在标称噪声干扰下,其位置和速度的均方根误差如图4所示.
显然,与博弈论滤波相比,扩展卡尔曼滤波和容积卡尔曼滤波存在相当大的估计误差.博弈论滤波导致位置均方根误差在8.35 m左右,而扩展卡尔曼滤波和容积卡尔曼滤波的平均位置误差分别为18.25和18.63 m(几乎是原来的2倍或更多).3种滤波方式下的平均速度误差分别为12.63,32.62和32.15 m/s.表3列出了3种过滤器的CRMSE和运行时间.
由图3(a)可以看出:博弈论滤波的位置CRMSE对于扩展卡尔曼滤波减少了32%,对于容积卡尔曼滤波减少了26%.如前所述,容积卡尔曼滤波的运行时间比博弈论滤波和扩展卡尔曼滤波长.
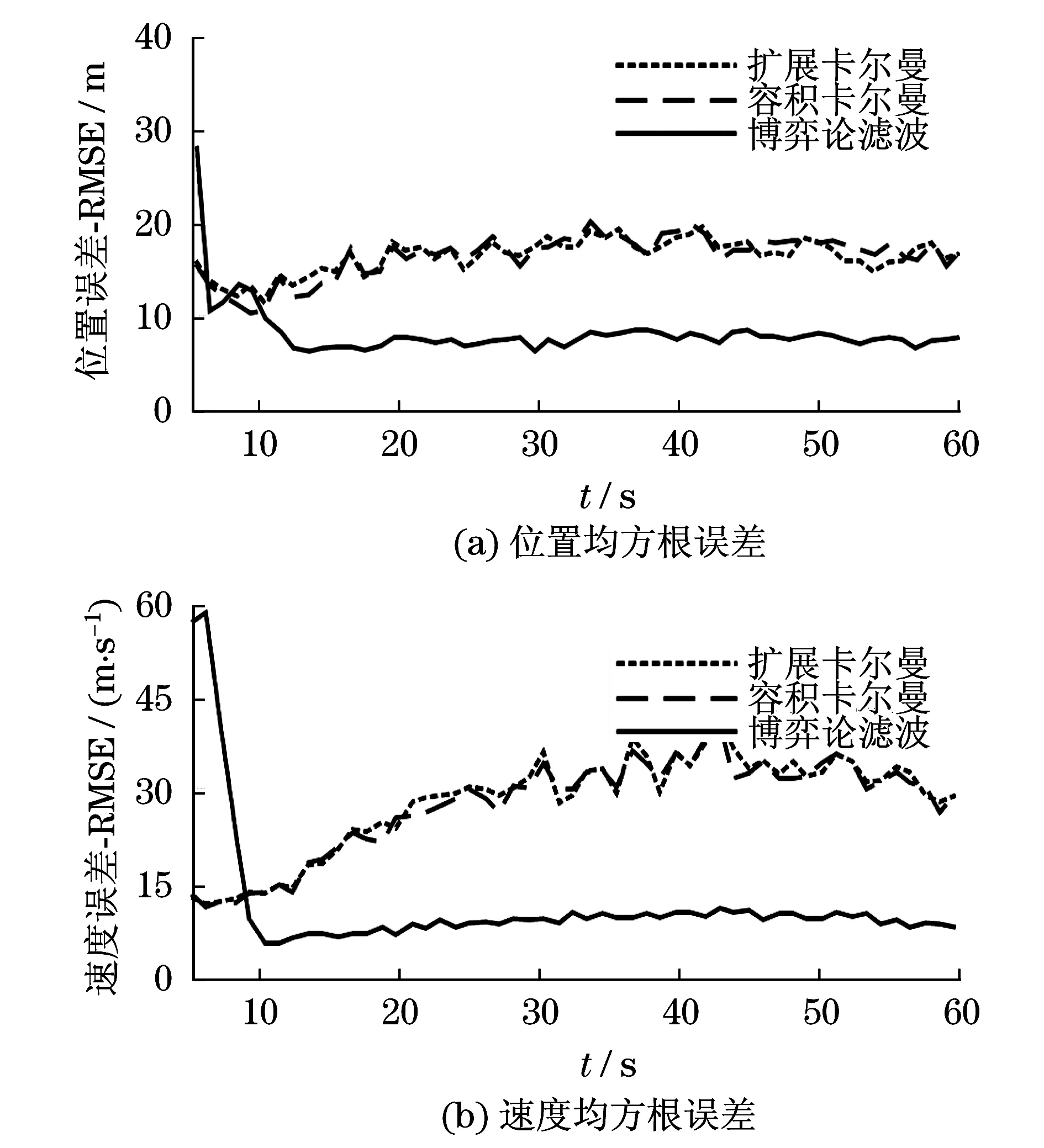
图4 标称噪声干扰下无人机恒定高度飞行跟踪误差Fig.4 Flight tracking error of unmanned acerial vehicle at constant heigth under nominal noise interference
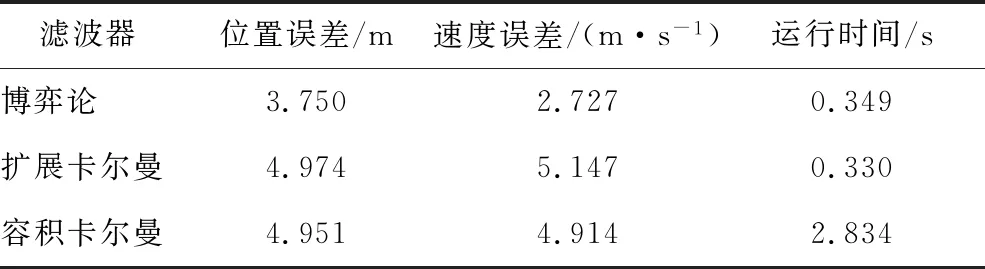
表3 标称噪声干扰下无人机恒定高度CRMSE及运行时间Tab.3 CRMSE and running time of unmanned acerial vehicle at constant height under nominal noise
3.3.2非标称噪声干扰
设置雷达传感器的测量噪声向量为零均值高斯序列,标准偏差为60 m,方位角为1.72°,红外传感器的测量噪声向量为零均值高斯序列,方位角和仰角的标准差为1.43°.模拟非标称噪声干扰下的跟踪效果,如图5所示.
由图5(a)可以看出:博弈论滤波产生的平均位置误差在40 m左右,而扩展卡尔曼滤波和容积卡尔曼滤波的平均位置误差分别为100.35和105.74 m.由图5(b)可以看出:博弈论滤波平均速度误差在45.62 m/s左右,而扩展卡尔曼滤波和容积卡尔曼滤波平均速度误差分别为113.52 m/s和105.26 m/s.另外,3种滤波器的状态估计和运行时间测试的CRMSE如表4所示.由表4可以看出:对于扩展卡尔曼滤波和容积卡尔曼滤波,博弈论滤波的CRMSE减少了46%.博弈论滤波的速度CRMSE对于扩展卡尔曼滤波和容积卡尔曼滤波均减少了53%.

图5 非标称噪声干扰下无人机恒定高度飞行跟踪误差Fig.5 Flight tracking error of unmanned acerial vehicle at constant height under nominal noise interference
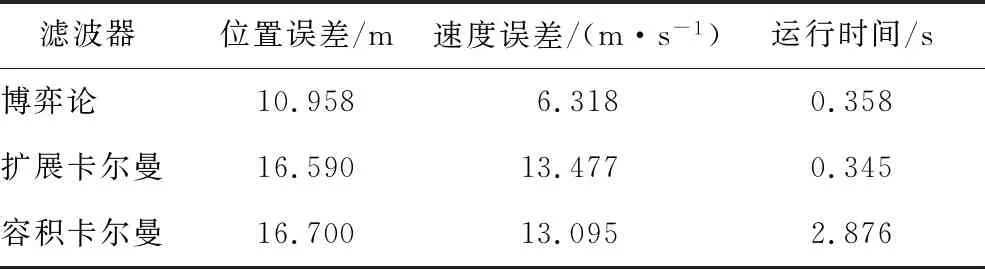
表4 标称噪声干扰下无人机恒定高度CRMSE及运行时间Tab.4 CRMSE and running time of unmanned acerial vehicle at constant height under nominal noise
4 结语
本文将博弈论滤波算法应用与雷达/红外无人机目标跟踪,将其描述为零和博弈,导出了博弈均衡点,以获得三维笛卡尔坐标系中无人机位置和速度的最佳估计.所提出滤波器增益可通过假设目标的最可能未知的转向命令来计算,使得其对目标的转向命令具有一定的鲁棒性.通过对变高度飞行和恒定高度飞行进行仿真,与扩展卡尔曼滤波和容积卡尔曼滤波相比,证明了博弈论滤波器的有效性和高精度性能.
——博弈论

