球形全向移动自平衡机器人的建模与控制
王江华, 张 莉, 曾建学
(华北科技学院 电子信息工程学院,河北 三河 065201)
0 引 言
轮式机器人按照平衡性能分类,可分为静态平衡机器人与动态平衡机器人两种[1]。静态平衡机器人一般具有3个以上的自由度,以保证机器人的静态稳定性,但由于自由度的增加,势必会造成驱动冗余,使得运动效率降低,同时由于机器人自由度的增加,使其对崎岖路面的适应性变差;相比之下,动态平衡机器人由于其自由度少于平面运动的自由度,导致其不稳定性增加,但随之而来的是灵活的运动特性和较高的运动效率。由于动态平衡机器人机构的独特性,必须采用独特的动态平衡原理才能实现正常运动。
本文所研究的球形全向移动自平衡机器人作为轮式机器人中的一种,由于其采用具有完整约束的全向轮,使其可以实现横向移动而不打滑,轻易在平面内实现3个自由度运动,具有全向移动的特点[2]。机器人采用一个球形轮作为驱动轮,外观上只具有一个自由度,因而其运动效率极高,理论上在任何路况中都能够保证与路面等接触。
该机器人理论原型为倒立摆,故也称为“倒立摆机器人”,区别于传统线性倒立摆,球形全向移动自平衡机器人将线性约束扩展为空间约束,这就对控制系统的稳定性与灵活性提出了更高的要求[3]。与传统机器人相比,球形全向移动自平衡机器人具有以下特点:① 依靠单个球形轮作为支撑轮,能轻易实现360°全向运动;② 可以实现0半径转弯;③ 依据轮式机器人对地面的连续接触性,故适用于全地形路面。
从理论研究角度,该机器人系统具有多变量、多驱动量、多自由度的特点,是一个极为复杂的MIMO非线性系统,再加上欠驱动的系统特性,可以为如今先进控制理论的验证和优化提供理想实验平台。对球形全向移动自平衡机器人的研究不仅对于提高机器人对复杂地形环境的适应能力具有现实意义,还推动了先进控制理论的研究应用。
本文从球形全向移动自平衡机器人运动原理着手,对机器人的逆Atlas球面运动平台(Inverse Atlas Spherical Motion Platform, IASMP)模型[5-6]进行分析,推导机器人运动控制方案;介绍机器人控制系统的设计和仿真模型的搭建,依据控制系统仿真模型,在Ballbot机器人上设计控制程序,以进行实物验证,检验机器人控制系统对实现机器人的直立控制与运动控制的合理性与有效性。
1 基于IASMP模型的运动学和动力学模型分析
由图1可知,Ballbot系列机器人使用3个直流无刷减速电机驱动3个全向轮,以控制机器人的球形轮,进而驱动机器人运动[4],这是一个典型的IASMP模型。研究将从IASMP模型出发,对机器人进行运动学和动力学模型分析。
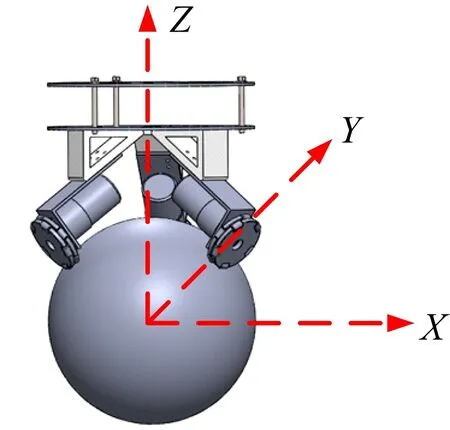
图1 机器人仿真设计图
机器人在不自旋的情况下,其运动可通过XOZ与YOZ两个正交平面实现。定义图1中YOZ平面中Y轴正向为机器人左向,定义XOZ平面中X轴正向为机器人前进方向。图2表示机器人全向轮与球形轮的位置关系,图中各参数的含义如表1所示。
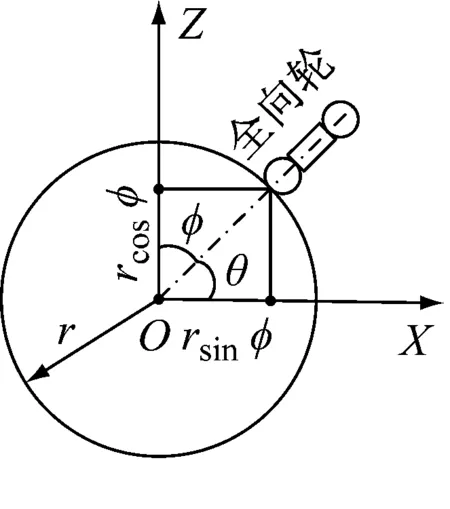
(a)

(b)
图2 机器人坐标系定义

表1 参数定义
机器人3个全向轮在机器人本体坐标系中的位置向量为P,方向为由坐标原点指向全向轮与球面接触点的方向[7]。实验机器人其全向轮与球面接触点和球心的连线与Z轴组成的倾角φ=45°
(1)
(2)
机器人采用双铝全向轮能够实现360°运动,具有旋转和侧身机动性。对全向轮速度进行分解,分为沿驱动方向的速度vs和垂直于驱动方向的速度vf。其中vf是球形轮转动所产生的速度,真正能够改变球形轮运动状态的是驱动方向的速度vs。故引出驱动向量si,按照图2所示的全向轮在机器人坐标系的位置,可得到3个全向轮的驱动方向:
(3)
至此可推导出全向轮沿驱动方向的速度vsv:
(4)
由式(4)即可得到各全向轮驱动方向的实时转速,对照图2,可得出机器人向X、Y方向的实时速度。
当轮子绕着Y轴旋转时,表示机器人正在沿前后方向运动,由图2可得其驱动方向的速度为:
(5)
当轮子绕着X轴旋转时,表示机器人正在沿左右方向运动,由图2可得其驱动方向的速度为:
(6)
若考虑机器人的自旋,则其绕Z轴驱动方向的速度为:
(7)
由式(5)~(7)得出机器人X、Y、Z3个方向的速度合成之后所得到的3个全向轮的最终速度vi为:
(8)
由于机器人滚球轮X、Y方向的球面线速度即是机器人当前的速度,故记:
(9)
则式(8)可改写成:
(10)
若设全向轮旋转角速度为ωi,由式(2)可推导出球形轮的角速度矢量Ω与全向轮旋转角速度的关系[8]:
(11)
式中,J表示机器人结构的雅可比矩阵,它将每个全向轮转动的角速度映射到球体的角速度。解算之后的逆雅可比矩阵和雅可比矩阵定义如下:
(12)
式中,rb和rw分别表示滚球轮与全向轮的驱动半径。由于仰角θ与天顶角φ之和是90°,即φ+θ=90°,由图2可见,同时由此即可得到:sinθ=cosφ,cosθ=sinφ。故解算之后的逆雅可比矩阵和雅可比矩阵又可以改写为:
(13)
故球体的角速度矢量Ω可由下式表出:
(14)
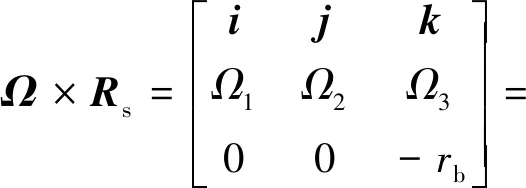
-rbΩ2i+rbΩ1j+0k=Vxi+Vyj+Vzk
(15)
故,对于机器人的速度V可表示如下:V=Vxi+Vyj+Vzk;其中3个分量:Vx,Vy,Vz在笛卡尔坐标系下可表示如下:
(16)
由式(16)可得三个速度分量的关系:
(17)
利用式(17)对时间的导数,可得到基于IASMP模型的运动学和动力学方程:
(18)
2 球形全向移动自平衡控制系统的设计
考虑到球形全向移动自平衡机器人与四轴飞控系统具有相似的特点,即非线性、强耦合、多变量等等[9]。因此,基于第1节对球形全向移动自平衡机器人的运动学分析,将四轴飞控的控制思路应用于机器人。
机器人控制部分,参考国外Pixhawk开源飞控,其旋翼控制部分主要采用串级PID控制技术,实现诸如误差校正、姿态解算、姿态控制、位置控制等等,并取得了较好的控制效果。
四旋翼通过4个电动机实现空间6自由度的运动,只需克服空气阻力(可以忽略不计)即可迅速改变机身姿态;而球形全向移动自平衡机器人则是通过3个直流无刷减速电动机,配合全向轮,通过无滑动的摩擦作用驱动球形轮,以实现机器人在平面上3自由度的运动。相比之下,四旋翼对于控制器的实时性、精确性要求更加严格;而对于该机器人,由于其控制输出需要通过静摩擦进行传递,期间必然存在一定的滞后性,对系统的实时性要求相对较低。基于以上对比分析,考虑通过串级PID技术,设计球形全向移动自平衡控制系统。
2.1 控制系统整体设计思路
基于对上一章机器人运动原理的分析,机器人控制可通过XOZ与YOZ两个正交平面实现。依据MPU6050运动传感器的轴向,以其水平X、Y轴对两个平面建立两套串级PID控制器,控制机器人的X、Y方向。根据运动传感器MPU6050的6轴数据,使用4元素法,通过卡尔曼滤波与互补融合,解算出3轴欧拉角输入X、Y方向的PID控制器的输出,依据式(10),将两个方向的PID控制器输出,映射到机器人3个电机上,以驱动球形轮实现机器人直立控制与全向移动。
2.2 机器人姿态控制方案
串级PID控制技术作为对传统适用于线性时不变系统的单级PID控制技术的改进,通过内外两环并联调节,大大提高了系统的抗干扰能力[10]。参考飞控控制思路,确定以球形全向移动自平衡机器人的角度环作为主控制回路,主回路设计角度PID调节器作为主调节器;角速度环作为副回路,设计角速度PID调节器作为副调节器。主回路使用由MPU6050运动传感器的6轴数据解算得到的3轴姿态角作为反馈信号,与设定值做差后作为主回路PID的输入。主回路的角度PID输出与角速度融合后直接作为副回路的输入,副回路PID调节器输出作用到执行机构[11]。
球形全向移动机器人串级PID控制系统框图如3所示。由图3可知,角度/角速度串级控制系统执行顺序是先执行角度控制,再执行角速度控制。为避免内外环产生共振,也考虑到进一步提高反应速度和工作频率,将系统角速度控制周期设为角度控制周期的一半,平均每5 ms角速度PID控制器进行一次控制更新,每10 ms角度PID控制器进行一次控制更新。如此设置,一来可以使得内环角速度对干扰能够进行快速而有效抑制,二来也将外环的误差对内环的影响降到最低,进一步增强了机器人系统的抗扰性。
2.3 机器人全向移动控制方案
对于运动控制,就四旋翼控制系统而言主要包括4个量:油门与3轴姿态角。由于空中运动的空间优势,使得其具有较大的可控制裕量,通过设定其姿态角,产生姿态偏差,在姿态控制器的调节下趋使其向某个特定方向运动[12]。而对于Ballbot机器人,其偏角的角度需要考虑驱动轮的驱动力,驱动力受重力分力的限制,若不外加支撑,其可调裕度非常有限,稍微控制不好就会导致控制失效。另外由于机器人的速度是根据3个电动机编码器解算得出的,该机器人又属于动稳定机器人,故其解算数值必然存在较大噪声[13]。但由于机器人对于控制的实时性要求较低,故本文通过中值滤波与均值滤波相互配合实现对机器人运动速度的测算。

图3 角度/角速度串级PID原理框图
基于此本文提出对已有的角度/角速度串级PID进行改进,在角度环外再加入速度环,将速度环的输出进行量程转换与当前反馈的姿态角进行叠加,共同作为角度环的输入,构成3闭环控制系统。即将速度控制转换成角度控制,通过直立环调节速度响应,使得控制作用更加平滑[14]。
机器人的运动控制框图如图4所示。

图4 机器人运动控制框图
3 机器人控制系统仿真模型的设计
机器人控制主要由X、Y方向的两个串级PID控制器组成,由于机器人结构的对称性,两个控制器设计方法基本一致,仅3个电动机对应X、Y两个方向的转向以及组合输出的比例有所不同。故仅从X方向控制器仿真模型的设计出发展开介绍。
机器人控制系统仿真模型的设计主要包括两部分:基于Matlab的SimMechanics工具箱设计机器人动力学仿真模型;机器人串级PID控制器Simulink仿真模型。
3.1 机器人动力学仿真模型
Matlab SimMechanics工具箱[15-16]主要用于多体动力机械系统及其控制的建模仿真。使用工具箱按照系统的运动机理,设计出对应的刚体、铰链、约束以及外力,以此搭建系统的刚体仿真模型,在仿真时,使用SimMechanics可视化工具,可将机构系统及其运动转化为直观的动画显示。区别于其他机械系统仿真软件,SimMechanics可以与Simulink结合,为控制系统的仿真设计提供了方便。
本文为简化模型,将3个全向轮直接转换为X、Y两个方向的作用力,对球形全向移动机器人建立SimMechanics模型如图5所示。
3.2 机器人控制系统仿真模型
机器人控制系统使用串级PID控制器进行设计,控制器由速度、角度、角速度组成3闭环控系统,控制器输出直接作用到机器人的动力学模型,得到各状态变量的反馈值,并送往控制器反馈端进行调节。机器人控制系统的Simulink仿真模型如图6所示。
3.3 机器人运动控制仿真
为验证机器人运动控制的有效性,设计验证试验,设置机器人初始参数:[0,0,0,0,0],即3个姿态角控制量均为0°,机器人两个控制方向的速度给定值为0。随后,给定X方向的速度设定值设定单个方波信号,观察机器人姿态角的变化。
由仿真结果可知(见图7),当给定信号发出后,机器人速度环输出引起机器人姿态变化,在姿态环的控制下,驱使机器人朝着X方向运动。当控制信号撤除后机器人能够及时矫正姿态,保持直立状态。由仿真结果可以看出,控制器能够完成设定任务。
4 实物验证
为进一步验证控制系统设计的合理性与有效性,本文根据控制器仿真模型,对Ballbot机器人设计实物验证。设计的机器人如图8所示。

图5 SimMechanics动力学模型图

图6 机器人控制系统仿真模型
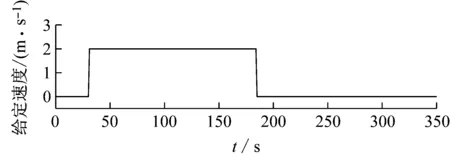

图7 运动控制器产生的姿态变化曲线

图8 Ballbot机器人实物图
本文所设计的实验分为两个部分,实验检验机器人姿态控制和机器人运动控制能力。
实验主要通过机器人机身运动传感器的3个姿态角(俯仰角Ax、翻滚角Ay、偏航角Az)反映机器人在静止状态下的平衡情况以及运动过程中的方向偏差情况;通过机器人的X、Y两个方向的速度(Vx、Vy)反映机器人定点直立、速度配合效果。机器人实物测试数据如图9所示。

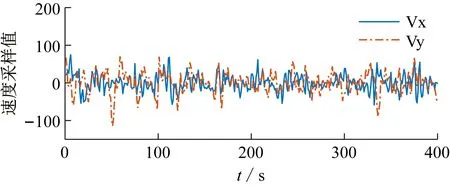
图9 姿态控制测试结果图
在姿态控制器的控制下,机器人上电初始化后,直接进入定点直立模式,不需要对机器人进行任何额外设定。通过机器人3个姿态角的变化曲线以及机器人速度变化曲线可看出:机器人一直在原地调整姿态,各姿态角度控制在3°以内,机器人的运动速度一直在原点附近波动,同时机器人X-Y方向上的速度也在x=0附近调整,保证机器人可以在原点保持直立。据此可判定机器人能够完成直立状态下的姿态控制。
机器人运动控制,主要通过测试机器人进行直线运动与圆周运动来检验机器人运动方向的准确性与速度控制的稳定性。机器人运动速度通过图10可以看出在进行直线运动与圆周运动时,机器人均能够平稳的调节运动速度以达到控制目的。
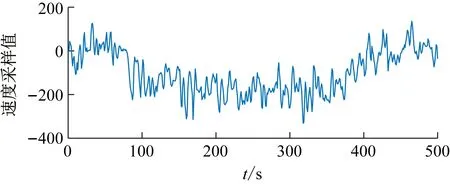
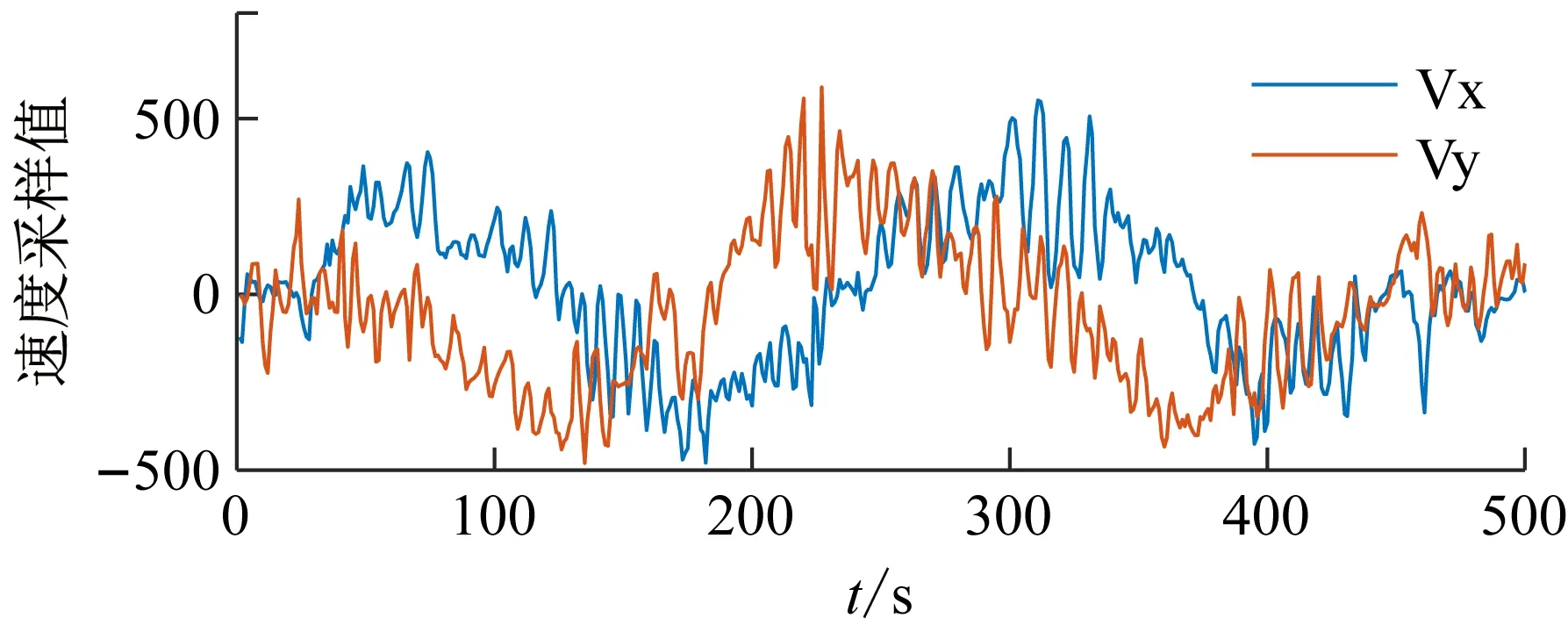
图10 运动控制速度曲线图
由图11所示,在机器人直线运动测试中,机器人Yaw轴的航向角变化曲线可知,机器人在运动过程中,其航向角变化在3°以内,可认为机器人运动方向稳定,体现出速度控制的有效性。
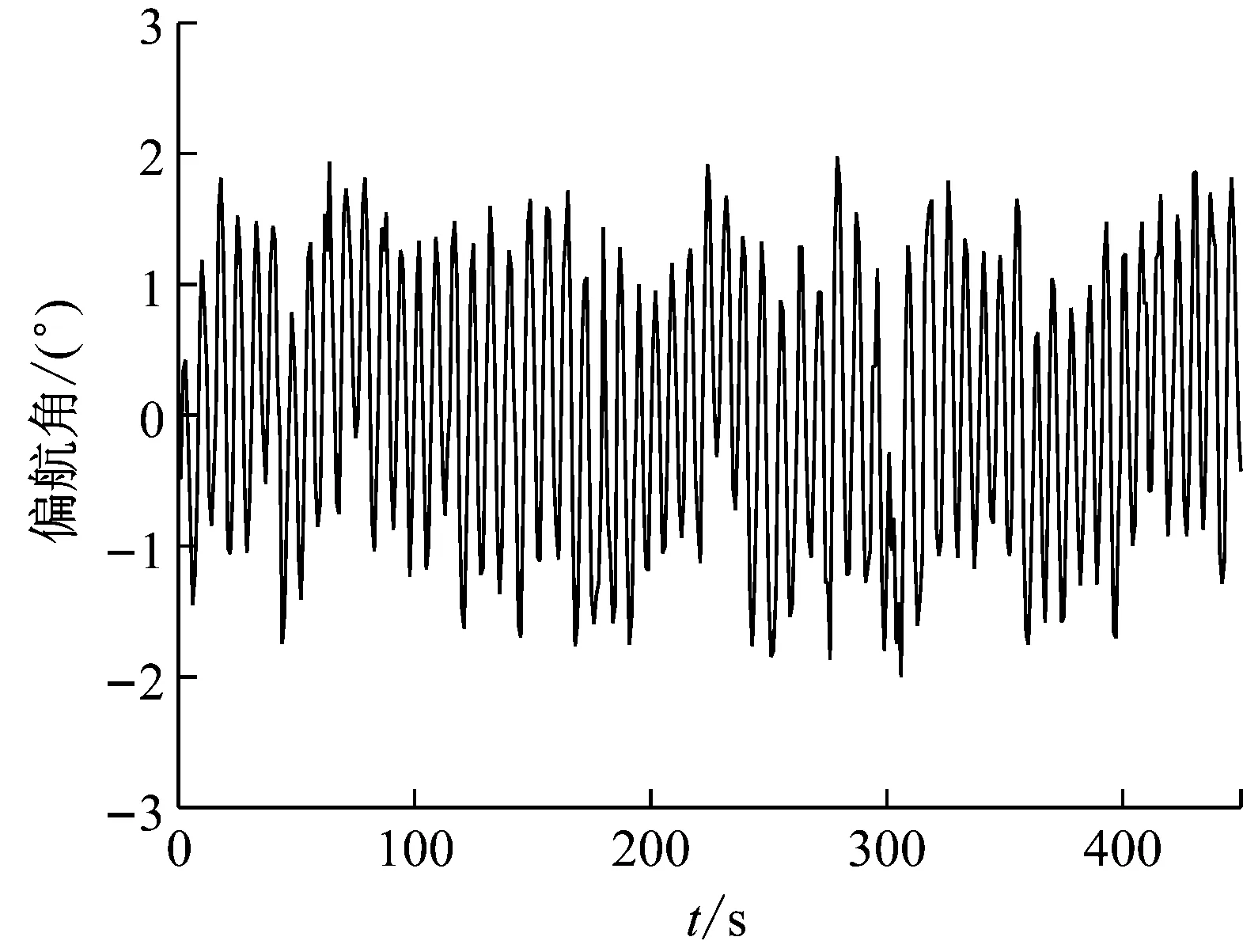
图11 机器人运动方向曲线图
5 结 语
本文重点研究球形全向移动自平衡机器人控制系统的设计。控制系统的控制对象是一种以运动高效性、灵活性为特点,并以单个球形轮作为运动轮的全向移动机器人(Ballbot机器人)。实现关键在于设计以串级PID技术作为控制方式的控制器,以实现机器人的直立和全向移动。
本文从机器人的IASMP模型出发,对机器人进行运动学和动力学分析,由此得出机器人3个无刷减速直流电动机的组合控制方案;并在SimMechanics工具箱设计机器人动力学仿真模型的基础上,设计机器人控制系统的Simulink模型进行仿真;同时按照仿真模型的设计方法,在实验室Ballbot机器人上设计软件控制器,实现了机器人定点直立与全向移动控制。
球形全向移动自平衡机器人控制系统具有多自由度、多驱动量、多传感器的特点,是一个极为复杂的MIMO非线性系统,再加上欠驱动的系统特性,可以为如今的先进控制理论的验证和优化提供理想实验平台。对球形全向移动自平衡机器人的研究不仅对于提高机器人对复杂地形环境的适应能力具有现实意义,也推动了先进控制理论的研究应用。

