基于准滑模控制的路径跟踪研究

李 伟，唐 峥，王洪民

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

随着科技进步和经济发展，汽车保有量迅速增加，非专业驾驶人员增多，道路交通事故的发生更加频繁，已经严重影响到人们的出行和生命财产安全。驾驶员注意力不集中是导致交通事故频发的重要原因之一。研究开发智能汽车有助于减轻驾驶员的劳动强度，提高车辆行驶安全性，减少道路交通事故和提高交通系统通行效率[1]。而智能驾驶汽车中的一个技术难点就是路径跟踪控制。智能驾驶汽车路径跟踪控制是指智能驾驶汽车的自动转向控制，其主要的目的是跟踪目标路径，同时保证车辆行驶安全性和乘坐舒适性[2]。它是智能驾驶汽车体系结构中的底层控制系统，其性能的好坏直接影响到智能汽车执行能力的优劣。当智能驾驶汽车的路径给定时，就要求汽车能够快速而准确的按照期望路径跟踪。其主要的内容是设计控制器确保汽车按照期望轨迹行驶，该期望轨迹由上位机通过车的传感器、通讯设备等获得的道路信息经过计算而得，设计的控制器与汽车的数学模型有关[3-4]。

目前智能汽车路径跟踪比较主流的算法一般有滑模控制，鲁棒控制，新型增量式PID控制以及强化学习自适应PID控制。滑膜控制方法是一种基于切换增益参数自调节的控制方法。其主要采用自适应滑模控制器实现了智能车辆的期望路径跟踪，并根据李雅普诺夫稳定理论消除了外部干扰和系统抖动[5]；鲁棒H输出反馈控制，在不考虑车辆横向速度的情况下实现了车辆的路径跟踪[6]；新型增量式PID控制算法，该方法可以相较于传统增量式PID算法，无人车路径跟踪的上升时间、调整时间均减小，响应速度加快，超调量减小，车辆实现快速稳定的路径跟踪[7]；强化学习自适应PID路径跟踪控制算法，该方法可以有效减小超调和震荡，可以较好地实现系统动态性和稳态误差性的优化[8]。

滑模控制的一个特点便是滑动模态可按需要而自行设定，当系统在滑模面运动时，系统的状态与对象参数的改变以及被控制系统的扰动相互独立，因此滑模控制系统具有较强的鲁棒性。然而，滑模控制的另一个特性是抖振问题，抖振问题是由滑模控制器的不连续开关特性而引起的。选用基于准滑模控制算法，从本质上较弱或者消除了抖振，从而可以很好的应用在实际中[7]。

建立二自由度车辆动力学模型、基于准滑模控制理论，设计准滑模路径跟踪控制器。建立基于二自由度车辆动力学模型的Simulink仿真模型，对车辆的路径跟踪控制策略进行离线仿真，并与传统的PID控制进行横向误差比较，仿真结果表明准滑模控制器具有更小的横向误差。利用dSPACE进行控制策略的硬件在环验证，仿真和实验结果表明所设计的控制器在追踪期望路径时具有较好的横向稳定性。

1 二自由度车辆动力学模型

下面以二自由度车辆动力学模型为例，如图1。

图1 二自由度车辆模型Fig. 1 Two-degree-of-freedom vehicle model

由牛顿第二定律和转矩平衡方程可得：

(1)

式中:m为质量，kg;U为车辆方向的速度,m/s;I为极惯性矩，(km·m2);Cr为后轮轮胎侧偏刚度，N/rad;Cf为前轮轮胎侧偏刚度，N/rad;v(t)为横向速度，m/s;a为质心至前轴的距离，m;b为质心至后轴的距离，m;δ(t)为方向盘转角，rad;ω(t)为车辆横摆角速度,rad/s;G为转向齿轮传动比。

将公式(1)改写为矩阵形式：

(2)

由图1可以求得车在X,Y轴上的速度为

(3)

式中：ψ(t)为车的横摆角，rad。

又横摆角非常小，所以式(3)可以写为

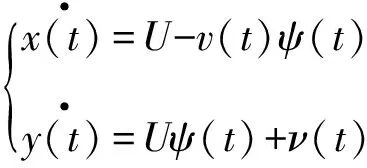
(4)

又

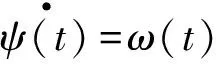
(5)

根据式(1)、式(4)、式(5)可以得出二自由度模型为

(6)

简写为如下形式

(7)

将式(7)的连续系统离散化，可得

X(k+1)=AX(k)+Bδ(k)

(8)

定义车的输出变量为

Z(k)=CX(k)

(9)

其中，

Z(k)=[v(k),ω(k),y(k),ψ(k)]T,

C=[1，0,0,0；0,1,0,0；0,0,1,0;0,0,0,1]T

2 基于准滑动模态的滑模控制设计

2.1 准滑模控制描述

为了解决滑动模块控制的抖动性，我们利用准滑动模态控制。所谓的准滑动模态，是指系统的运动轨迹被限制在理想滑动模块的某一领域内的模态。从理想轨迹方面来说，具有理想滑动模态的控制是使一定范围内的状态点均被吸引至切换面。而准滑动模态控制则是使一定范围内的状态点均被吸引至切换面的某一领域内，通常称此领域为滑模切换面的边界层[9]。

在边界层内，准滑动模态不要求满足滑动模态的存在条件，因此准滑动模态不要求在切换面上进行控制结构的切换。他可以在边界上进行结构变换的控制系统，也可以是根本不进行结构变换的连续状态反馈控制系统。准滑动模态控制在实现上的这种差别，使它从根本上避免或削弱了抖振，从而在实际中得到了广泛的应用[9]。

2.2 基于准滑模控制的位置跟踪

2.2.1 滑模面的参数设计

针对线性系统

(10)

滑模面设计为

(11)

式中：x为状态向量；C=[c1…cn-11]T。

在滑模控制中，参数c1,c2,…,cn-1应满足多项式

pn-1+cn-1pn-2+…+c2p+c1为Hurwitz，其中，p为Laplace算子。

2.2.2 滑模控制的工程意义

针对路径跟踪问题，设计滑模函数为

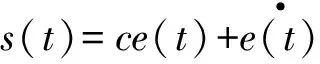
(12)

收敛结果为

e(t)=e(0)exp(-ct)

(13)

即当t→∞时，误差指数收敛于0，收敛速度取决于c值。

如果通过控制律的设计，保证s(t)指数收敛于0，则当t→∞时，误差变化率也是指数收敛于0。

2.2.3 基于准滑模控制的路径跟踪控制律推导

由车辆二自由度转化模型可知，车辆侧向位置的变化率为

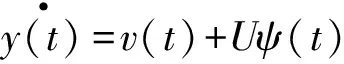
(14)

(15)

取位置指令为值yd(t)，那么e=y-yd为跟踪误差。

并且

(16)

定义跟踪误差函数s为

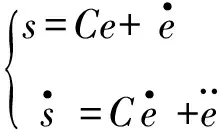
(17)

C为滑模面参数，且C>0,故:

(18)

采用指数趋近律，有：

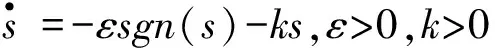
(19)

结合式(16)和式(17)，得：

(20)

利用饱和函数sat(s)代替理想滑动模态中的符号函数sgn(s)。

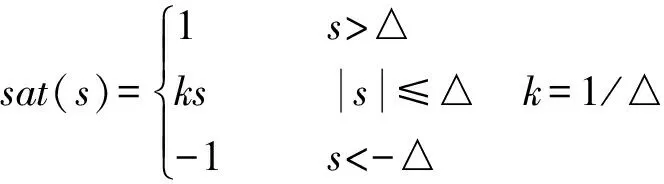
(21)

其中△=0.8

结合式(5)和式(20)，所以转向盘控制律为

(22)

3 路径跟踪仿真

蛇形线是常用的评价汽车操纵稳定性的典型道路模型，为模拟汽车的路径跟踪情况，采用蛇形线作为理想的道路模型输入。取道路轨迹为实际道路中心线的轨迹。

3.1 蛇形线路径跟踪仿真

蛇形线试验道路模型尺寸如图2。

图2 蛇形线道路模型Fig. 2 Serpentine road model

图2中各段的参数为：S0=L=2U；5L=10U；S=3U；B=2.46 m。其中U为车的速度；B为标杆宽度。驾驶员实际的跟踪轨迹如图3所示的经过三次样条拟合得到的一阶导数连续的三阶曲线。

因此，蛇形线的道路模型为

(23)

图3 蛇形线路径Fig. 3 Serpentine path

编写基于准滑动模态控制位置跟踪算法，建立Simulink仿真模型。

汽车整车参数如表1：

表1 汽车整车参数Table 1 Vehicle parameters

3.2 仿真结果

为了验证该算法对于路径跟踪控制的优劣性，我们引入工程中常用的PID控制进行对比试验，下面是PID控制的路径跟踪误差。

图4和图5反映了路径跟踪的结果和绝对误差，仿真结果表明准滑模路径跟踪控制在车辆追踪期望路径时具有较好的横向稳定性。

图5和图6分别是滑模控制和PID控制的路径跟踪结果偏差，结果显示滑模控制的路径跟踪结果偏差比PID控制要好。

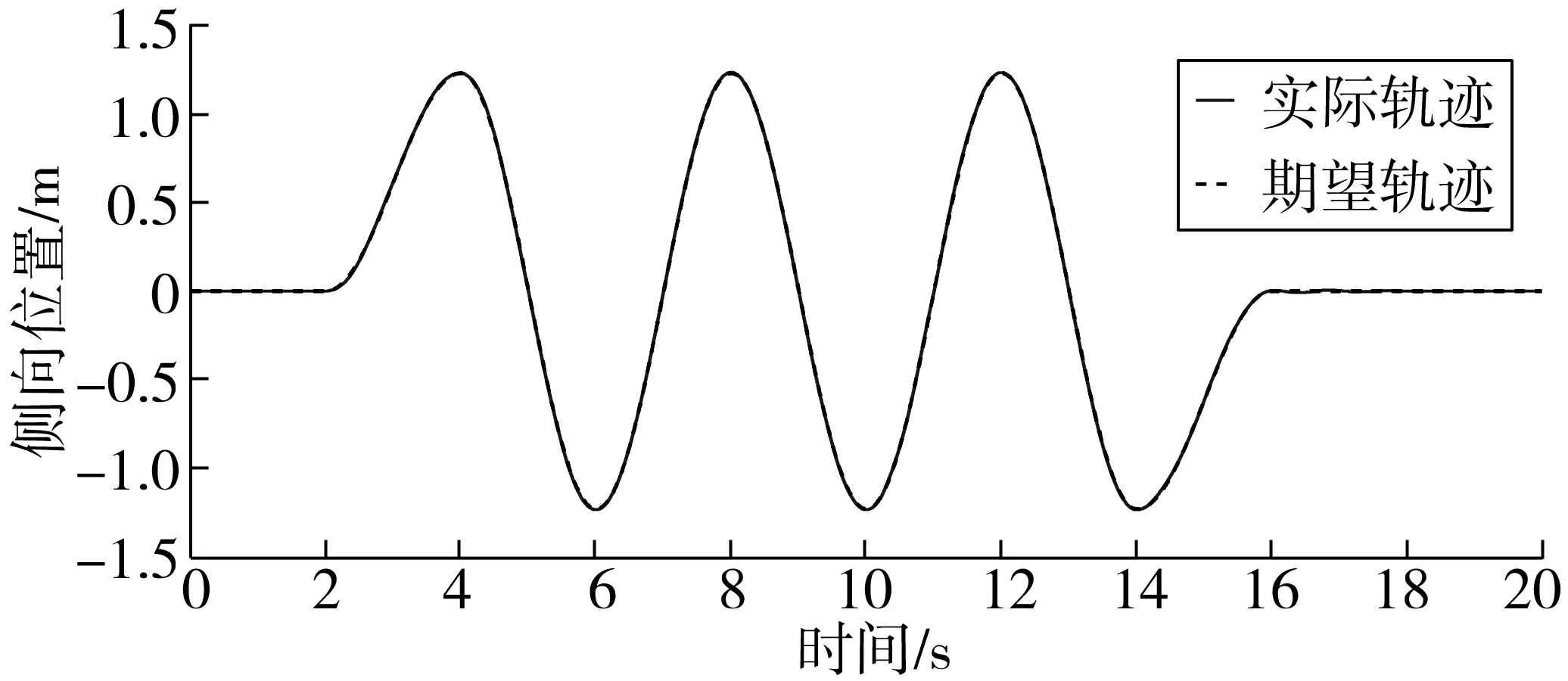
图4 侧向位置跟踪结果Fig. 4 Lateral position tracking results

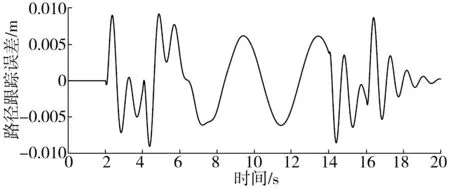
图5 蛇形线路径跟踪结果偏差Fig. 5 Tracking result deviation of serpentine path

图6 PID路径跟踪结果偏差Fig. 6 PID path tracking result deviation

4 硬件在环实验

4.1 硬件在环实验台搭建

硬件在环(hardware-in-the-loop)仿真测试系统是把控制程序直接烧结进处理器从而运行仿真模型来模拟受控对象的运行状态[10]，我们这里用AutoBox仿真器代替实车，其通过一系列数学模型模拟车辆的动力系统。

为了测试准滑模变结构路径跟踪性能的优劣，搭建dSPACE HIL仿真试验台。本次实验是在清华大学恒隆转向研究所的实验室里面进行。借助其实验设备完成了本次硬件在环实验。

如图7，其包含有dSPACE仿真器、上位机及电机、传感器、驱动板和执行机构。该dSPACE仿真器通过CAN总线与上位机相连，可以将实时仿真模型导入仿真设备中并控制模拟过程。

图7 路径跟踪硬件在环实验台Fig. 7 Hardware-in-the-loop experimental platform for path tracking

建立硬件在环Simulink模型，设备中的dSPACE ASM模型与dSPACE I/O版通过RTI模块相互连接, dSPACE/Simulink模型可用于快速原型开发，自动产生C代码烧结到实时硬件中，实现对该模型的快速控制。

4.2 仿真结果和硬件在环实验结果对比

图8给出了理想轨迹、车辆侧向位置响应的仿真结果和硬件在环实验结果，结果表明车辆在笔者所采用的控制策略下具有较高的路径跟踪控制精度。

图9和图10为横摆角速度和侧向速度仿真结果和硬件在环实验结果，结果显示笔者所采用的路径跟踪控制策略能保证车辆在路径跟踪过程中具有较好的横向稳定性。

图11给出了在路径跟踪过程中方向盘转角变化的仿真结果和硬件在环实验结果；图12给出了车辆横摆角响应的仿真和硬件在环结果。

图8 侧向位置跟踪结果Fig. 8 Lateral position tracking results

图9 横摆角速度响应曲线Fig. 9 The yaw rate response curve

图10 侧向速度响应曲线Fig. 10 Lateral speed response curve

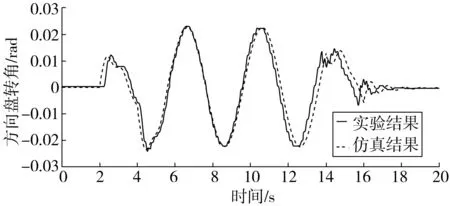
图11 方向盘转角响应曲线Fig. 11 Steering wheel angle response curve

图12 横摆角响应曲线Fig. 12 The yaw response curve

5 结 语

综上可得，仿真和硬件在环实验结果均表明准滑模路径跟踪控制能使车辆追踪期望路径时具有较好的横向稳定性。

从对比图还可以看出，仿真结果和实验结果还是存在一定的偏差，原因可能有以下几点：数据之间的传输用CAN通信，CAN信号从发送经过执行机构之间的传输会产生一定的延迟；执行器本身的特性，比如执行机构之间存在机械摩擦；外界环境的干扰等。这些都会造成实验结果与仿真结果之间的偏差。