波罗的海干散货航运指数混沌特性分析
杨 蕾,张厚保
(中国交通通信信息中心,北京 100011)
1 BDI 指数与混沌
BDI 指数由波罗的海航运交易所发布,一直以来都反映国际干散货航运市场的整体态势,被称为“晴雨表”。BDI 指数的计算以11条干散货航线的运价为基础,按照一定的权重对每一条航线的运价进行加权平均而得出。它代表了干散货航运市场的运价水平。在航运市场具有很高的权威性。
所谓混沌,指的是金融系统中一种看似无序实则有序的状态。它是一种非线性的存在形式,具有混沌属性的系统有着非常深层次的有序的结构规则,并且表现出特定的周期性和对称性。
2 数据来源与处理
本文基于相空间重构理论对波罗的海干散货航运价格系统进行混沌分析。数据源选取波动较大的1999年11月3日至2013年3月24日的BDI指数,数据样本量为3,351个,数据来源为克拉克森官网。此时间段的数据波动情况如图1所示。
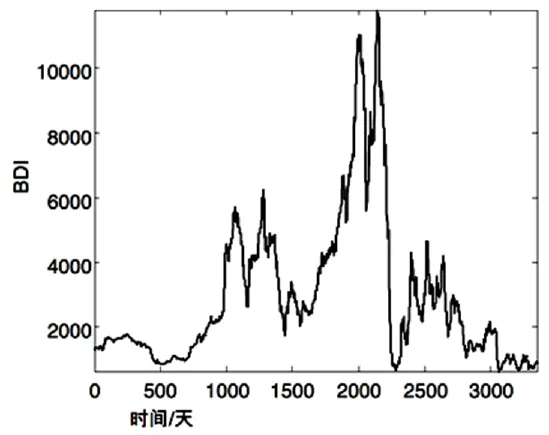
图1 BDI指数
3 BDI 指数相空间重构
相空间重构技术是目前混沌识别主要工具,主要被应用于工程领域处理复杂系统。相空间重构技术核心的理论依托是:复杂系统内部各个状态之间是相互影响的,每个状态都是由与之关联的其他状态分量演化决定。因此系统的每个状态都存于某个分量的发展中。选取合适的时间延迟和嵌入维度,就能够重构出系统的完全面貌。
确定时间延迟τ 与嵌入维数m,对波罗的海干散货航运价格系统进行相空间重构。
3.1 延迟时间的确定
互信息法是最常用的求延迟时间的方法。利用互信息法求某个时间序列Xn=(x1,x2,…,xn),的延迟时间,见下式:
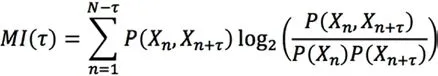
式中,时间序列Xn的概率密度是P(Xn),Xn与X(n+τ)的联合概率密度是P(Xn,X(n+τ))。
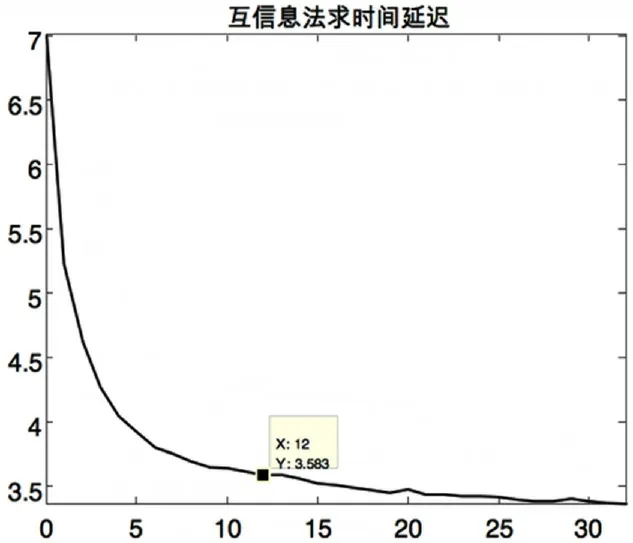
图2 时间延迟
由图2可以看出,第一个最小值出现于12,因此延迟时间为12。
3.2 嵌入维数的确定
系统混沌识别的另一个重要步骤是选择恰当的嵌入维数。过大的嵌入维数需要更多的数据支撑和计算资源,过小的嵌入维数又不足以反映出系统内在的情况。
本文选取CAO 方法求系统的最佳嵌入维数。
式中,‖·‖为向量的范数,常用的范数为‖Xk(m)-Xl(m)‖=max0≤j≤m-1|xk+jτ-xl+jτ|;Xn(i,m)(m)为上述范数定义下,距Xi(m+1)最近的向量。如果Xn(i,m)(m)与Xi(m+1)相等,则按照范数的定义寻找另一个最近的向量。
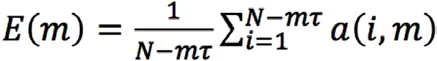
式中,E(m)为a(i,m)的均值。令E1(m)=E(m+1)/E(m),检测E(m)的变化。当m 大于m0时,E(m)保持不变,m0+1即为最合适的嵌入维。
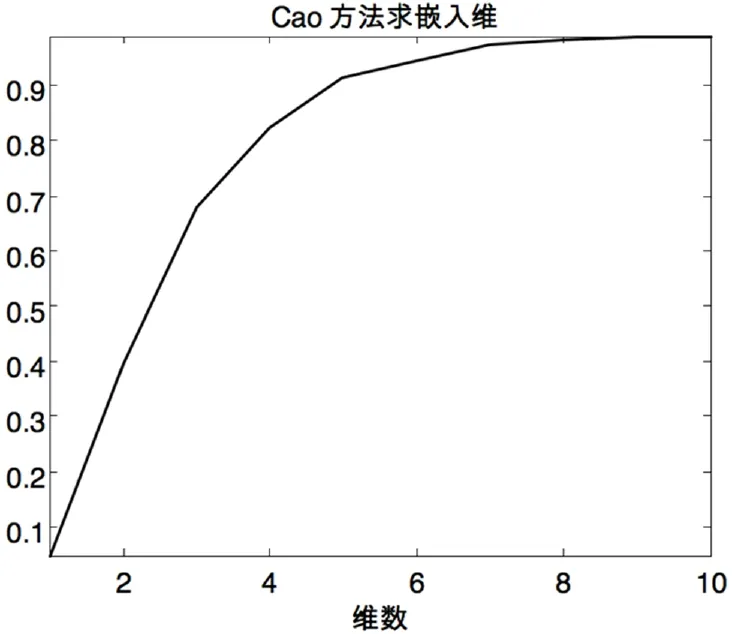
图3 嵌入维
如图3所示,可以看出当维数为9时,E(m)保持稳定,不再变化,所以9为最佳嵌入维数。
4 干散货运价系统混沌状态的识别
本文选取李雅普诺夫(Lyapunov)指数法为混沌识别方法。1983年,数学家格里波基证明:某个时间序列的最大李雅普诺夫(Lyapunov)指数大于或等于零,即可证明该系统存在混沌属性。
假设存嵌入维数m,时间延迟为τ 的时间序列Xn=(x1,x2,…,xn),重构其相空间:
Y(t)={x(t),x(t+τ),…,x[t+(m-1)τ]},(t=1,2,…,M)M=N-(m-1)τ
对该序列进行相空间重构后,选取一点Y(t),同时选择与Y(t)的绝对距离小于ε 的若干个临近点。如下式:
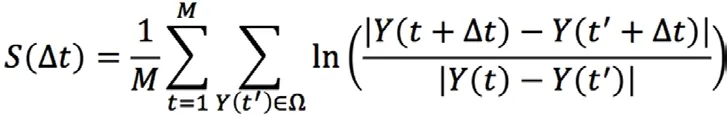
式中,Ω 是与临近点的集合;S 为预测误差;Δt 为预测的时间。通过对S 关于Δt 函数的图像指数拟合,得出λ 即为该序列的最大Lyapunov 指数。
S=eλΔt
对嵌入维9,延迟时间12的BDI 指数序列进行相空间重构,做出函数图像,如图4所示:
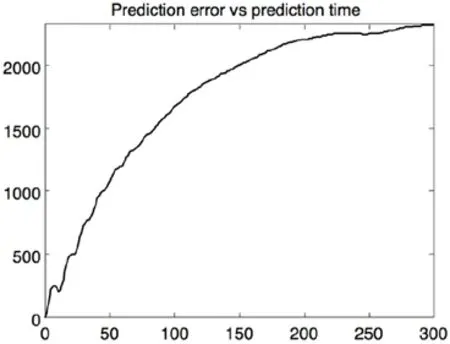
图4 李雅谱诺夫指数
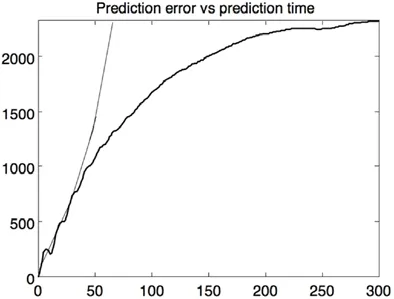
图5 拟合结
最后对该函数进行指数拟合,如图5:S=e0.1542Δt,得出最大Lyapunov指数为0.1542。因此,国际干散货运价系统具有混沌特性。
5 结束语
本文的研究结果说明:一是国际干散货运价系统具有混沌特性;二是波罗的海干散货运价指数与世界经济息息相关,受经济影响明显;三是借助金融手段对干散货运价系统进行干预,可以降低航运市场的金融风险。本文的研究结论对于干散货航运市场的有效监管具有一定的借鉴意义,发挥好BDI 指数“晴雨表”的作用,借助金融手段有效干预航运市场,对于稳定市场秩序具有重要意义。

