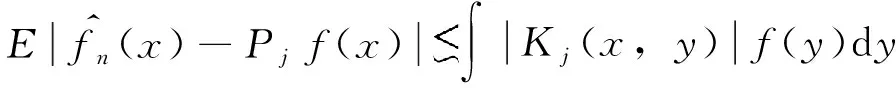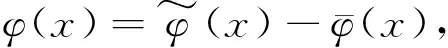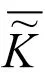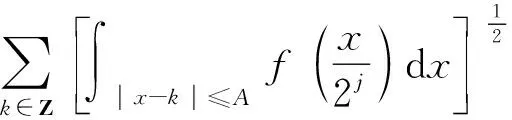NA样本密度小波估计的相合性

许俊莲

(宝鸡文理学院数学与信息科学学院，陕西 宝鸡 721013)

小波分析的一个重要应用是非参数密度估计。设X是连续型随机变量，它服从的概率密度函数f(x)未知。 经典的密度估计问题是: 如何通过n个同分布的随机样本X1,X2,,Xn定义恰当的估计器fn使其在某种意义下逼近f。关于独立同分布随机变量序列的概率密度函数的估计问题已经得到了完善的结论[1-3]。在可靠性理论，渗透理论和某些多元分析问题中，随机变量往往不是独立的，而是具有一定的相关性，负相协随机变量就是一类常见的相关随机变量。1981年， Alam等[4]首次提出了负相协随机变量的概念：

定义1称随机变量X1,X2,,Xn是负相协的(negatively associated，简记为NA)，如果对于集合{1,2,,n}的任意两个不相交的非空子集A和B，

Cov(h1(Xi,i∈A),h2(Xj,j∈B))≤0

其中h1和h2是任意两个关于每个自变量非降(非增)的多元函数，Cov(X,Y)表示随机变量X与Y的协方差。

显然，独立随机变量是负相协的。随后， Joag-Dev等[5]对于负相协随机变量做了更深入的研究，得到了一系列常用性质：

性质1[5]设随机变量X1,X2,,Xn是NA的，任给集合{1,2,,n}的m个两两不相交的子集A1,A2,,Am以及m个单调关于每个变元非降(非增)函数f1,f2,,fm，则随机变量f1(Xi,i∈A1)，f2(Xj,j∈A2),,fm(Xk,k∈Am)仍然是NA的。

性质2[5]设X,Y是NA随机变量，则E(XY)≤(EX)(EY)。

近些年来，鉴于负相协随机变量的重要性，该样本下密度函数的估计问题也引起了一批学者的关注。李永明等[6]、杨善朝[7]分别用核方法和最邻近估计方法讨论密度估计的相合性问题。此外，针对噪声密度估计模型，Chesneau等[8]利用小波方法讨论了NA样本下密度的估计问题。在此基础上，文献[9-12]做了进一步的讨论研究。

鉴于小波估计器的良好表现，本文将讨论负相协样本下概率密度函数的估计问题。具体地，利用小波方法定义线性小波估计器。进一步，在不假定密度函数具有任何光滑性的条件下，证明该估计器的Lp,1≤p≤∞平均相合性。首先给出本文涉及到的小波分析中的几个基本概念。

定义2[13]平方可积函数空间L2(R)中的多分辨率分析(multiresolution analysis，简记为MRA) 是指满足以下条件的一列线性闭子空间{Vj}j∈Z:

(i) 单调性:Vj⊆Vj+1,j∈Z;

(iii) 伸缩性:f(x)∈V0⟺f(2jx)∈Vj,∀j∈Z;

(iv) 基的存在性: 存在φ∈L2(R)，使得{φ(x-k)}k∈Z为V0的标准正交基，其中φ称为该MRA对应的尺度函数。

(1)

定义4[14]尺度函数φ满足S条件是指存在有界径向非增函数Φ使得

|φ(x)|≤Φ(|x|)(a.e.)

且

当尺度函数φ满足(θ)条件时，

绝对收敛。从而正交投影核

满足

(2)

正交小波基的重要性在于它不仅是L2(R)中的标准正交基，而且在一定条件下也是Lp(R)(1

注意到，φ满足(θ)条件蕴含φ∈L(R)∩L∞(R)，从而φ∈Lp(R),1≤p≤∞。另一方面，S条件可推出(θ)条件(见文献[14]，引理8.5)。

1 若干引理

首先给出本文用到的几个相关引理。

特别地，当u(x)=v(x)=φ(x)时，下述结论成立：

Su等[15]将独立随机变量的Rosenthal不等式做了推广，得到了NA情形下的Rosenthal不等式。

2 主要结论

其中

下面给出本文的主要定理，为了定理证明的需要，选取尺度函数φ是紧支有界变差函数且满足S条件。为了方便，不妨假定φ的支撑集含于集合[-A,A]中。

(3)

注意到|Kj(x,y)|≤2jF(2j(x-y))，那么，

=Aj(x)+B(x)

(4)

且

所以Lebesgue控制收敛定理蕴含

(5)

定义

(6)

(7)

(8)

(9)

类似地，

(10)

将式(7)-(10)代入式(6)，利用Jensen 不等式有

(11)

其中

根据式(4)和式(11)，

(12)

证明注意到

(13)

(14)

从而，

这样，式(14)化为

(15)

当p≥2时，由Rosenthal及Jensen不等式可知

因此，

故

(16)

(17)

(18)

将式(16)～(18)代入式(15)，有

(19)

以及

从而，式(13)在1

再利用f(x)≤ω|x|，得

(20)

结合式(20)，有

(21)

(22)

从而

(23)

则

(24)

根据Jensen不等式及性质2，我们有

(25)

因为

结合式(25)和(21)得