从两个乘法公式的教学浅析学生运算素养的培养
□余志渊 张晓斌
(重庆市第一中学校,重庆 400030;重庆市教育科学研究院,重庆 400015)
一、问题的提出
小学数学计算主要涉及数的运算,从认识上比较单一具体,进入初中,用字母表示数,大量的数学符号出现,学生感到数学突然变得难以捉摸,难以理解,在小学认为很简单的运算在初中反而变得很难;另一方面,教师在教学过程中也感觉到,不管自己怎样细致地讲解,耐心地指导,学生在计算上仍然存在很大问题.所以,在日常教学中怎样培养和提高学生的计算能力,是我们不得不考虑的问题.下面通过具体的教学案例,谈谈我们在培养和提高学生数学运算素养方面的一些做法.
二、学生运算错误原因分析
搞清楚学生在运算方面存在的问题,是培养和提高学生运算能力的前提.通过对学生的习题错误进行分析,主要有以下几种因素导致学生运算错误率较高,运算素养不高.
(一)缺乏对公式的正确认识
我们先来看学生常见的一些错误案例.
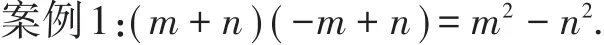
此错误的原因是对平方差公式的结构认识表面化,认为就是用第一项的平方减去第二项的平方,没有真正认识到是用相同的项的平方减去相反的项的平方.
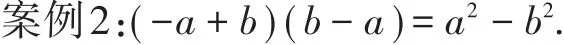
此错误的原因是没有搞清楚平方差公式适用的条件.

此错误的原因是受“积的乘方”公式影响,在定式思维影响下,想当然地造出这个错误公式.在平时的教学中这种错误出现次数很多,学生要经过多次讲解、强调,反复练习,才能逐渐消除.
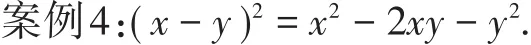
此错误的原因是受定式思维的影响,因为在平时的教学中,我们非常强调负号参与运算时要注意结果的符号问题,这里学生受这种思维的影响,自然刻意地去想结果也应是负号.
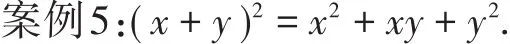
此错误的原因是没有认清公式结构,认为左边各项系数都是数学1,右边各项系数也不会有其他数字出现.
以上错误充分说明学生对基本概念、公式、法则的认识是非常模糊的,试想学生连公式的基本结构、公式适用的基本条件都没有搞清楚,错误自然难以避免.
(二)缺乏对数学思想方法的认识
进入七年级的学生,对数学思想方法的认识很薄弱,基本上不知道有数学思想方法这一概念,由于不具备基本数学思想方法作指导,学生在处理一些题目时往往无从下手,即使听教师讲解也难于理解,难以转化成自己的解题经验.下面通过几个具体的案例来说明.
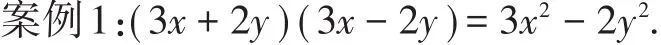
此错误的原因是缺乏整体思想,没有分别将3x,2y看作是一个整体.
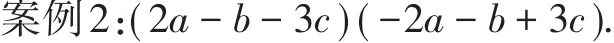
此题学生往往难于下手,最后只有用多项式乘法法则进行运算,但较为烦琐,利用整体思想,将式子重新组合为[-b+(2a-3c)][-b-(2a-3c)],再利用平方差公式,运算就非常简便了.
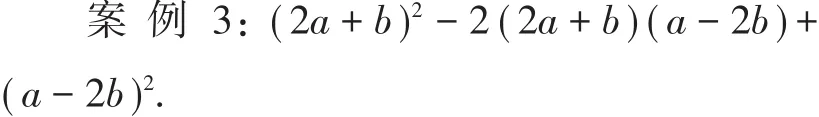
此题学生往往不会将(2a+b),(a-2b)分别看作一个整体,再利用完全平方公式得到[(2a+b)-(a-2b)]2,从而简化运算,而是直接利用乘法公式和乘法法则进行运算.
以上题目,因为学生没有利用有效的方法将计算简化,以致运算量过大,导致错误率上升.
(三)缺乏较好的运算习惯
通过对学生运算过程的观察,发现学生在运算习惯上存在一定问题.
首先,没有认真审题的习惯,许多学生一拿到题就开始算,没有认真观察算式的结构,找出简便的算法,这样往往使运算量增大,导致错误率上升.
第二,在做题过程中没有对易错点进行短暂停顿、进行查误的习惯,只是一味地继续往下面算,往往因为一个环节的错误导致整个题目的错误.
(四)缺乏良好的心理因素
学生数学运算素养与学生的心理因素有一定关系,学生心理所呈现的这些特征,往往是有意识的.有时虽然教师指出其错误答案,但不知道自己错误的真正原因.
第一,定式思维中的消极因素往往影响学生对概念、公式、法则的正确认识,从而导致运算在数学本源上的错误.
第二,缺乏自我评价意识,只要找到一种算法就一直死算下去,而不再考虑算法是否合理、简捷,往往因运算量大而使错误率提高.
第三,受记忆还原影响,当学生对新的知识掌握不扎实,就容易被原来相近的知识所取代,从而造成新旧知识的混淆,对基础知识的认识模糊,导致运算的错误.
三、培养和提高学生数学运算素养的教学思考
(一)加强对基本概念、公式、法则的教学
培养学生运算素养的首要前提是让学生准确掌握数学概念、公式、法则.这些概念、公式、法则有的是运算的依据,有的是运算的步骤,综合起来就是运算的行为准则.我们在教学时,应该注重公式的推导过程,注重从不同的角度验证公式,总结出公式的适用条件,分析公式的结构特点,利用正反例加深对概念、公式的认识,多角度、多侧面地让学生认识公式.
(二)科学有序地组织学生对公式进行应用
我国心理学家冯忠良教授认为,一般心智技能的形成分为三个阶段,即活动模式定向阶段、活动模式操作阶段、活动模式内化阶段[1].运算技能的训练与之对应的三个阶段是:(1)模仿练习阶段:在例题示范下进行练习,所选习题难度不大,变化不大,要求学生直接套用公式,保证结果的正确性;(2)变式练习阶段:在学生初步掌握知识和技能的基础上组织练习,习题难度适当提高,要求学生在求得正确答案后,对运算的过程、依据、方法进行总结与概括,促使操作方式上升到理性水平;(3)综合练习阶段:此时可选择具有一定难度的综合题,训练学生确定运算方向,灵活运用运算法则的能力[2].
教学实例:“平方差公式”的应用,即例题、习题设计.
通过对“平方差公式”基本结构部分的教学,学生对公式有了一定的认识,接着通过例题和巩固、变式等练习加深对公式的认识.
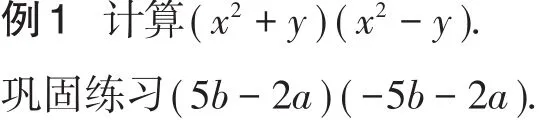
此例题是对公式的直接应用,起到再次熟悉公式的目的.
例2简便计算79×81.
此例题是训练学生思维的灵活性,学生在习惯字母运算的同时,通过这个例题让学生的思维在字母和数字之间灵活转换.
变式练习1:计算1002-992+982-972+…+22-12.
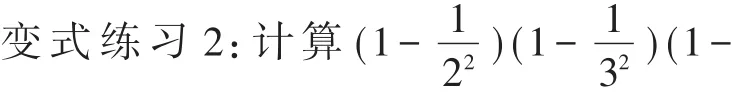
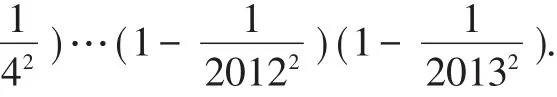
以上例题都是对平方差公式的综合(正向和逆向)应用,在难度上逐渐提高,通过例题讲解和变式练习,让学生了解并熟悉这些题目结构,并逐渐掌握解决这些题目的思路和方法.
(三)切实做到练习中的两个重视
第一,重视练习效果的及时反馈.心理学研究表明,如果对正在进行技能训练的学生及时提供训练结果的反馈信息,如每次练习的得分,练习过程中不断给予鼓励,分析练习中出现的错误等,练习效果就会显著提高[3].因此,在平时的教学中,要及时批改学生作业;及时讲评学生作业中出现错误较多的题目;多与学生交流,了解他们在做题过程中的真实想法,并给予评价和指导.
第二,重视学生练习的自我纠错.建构主义学说认为,数学学习活动是一个以学生已有的知识和经验(已有的认知结构)为基础的主动建构过程[4].因此,让学生经历自我发现错误并且自我改正错误的过程,是提高运算能力的必要措施.在平时教学过程中,多让学生上讲台板书解题过程,引导学生发现解题过程中的得与失;严格落实学生的改错过程,采取有效办法帮助学生纠正错误.
(四)使学生养成对知识进行总结的习惯
在平时的教学过程中,发现学生普遍缺乏对所学知识进行总结的习惯.在运算上经常出现同样错误反复出错的现象;对一些较难题的解答也不稳定,前面刚做过,后面遇到又不知道该怎么算了.因此,引导学生将所学知识进行总结、归纳、反思,是培养和提高学生运算能力的重要方法.
教学实例:“完全平方公式”的复习总结教学.
(1)对公式结构的总结与观察:

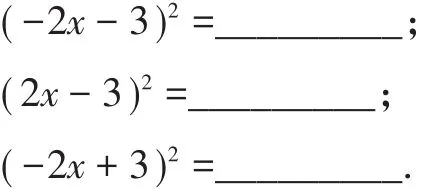
学生在直接用完全平方公式时,若首项系数为负数时容易出错,引导学生认真观察分析发现:两项同号时就用“和”的公式,两项异号时就用“差”的公式.
(2)对公式推广的总结:将两项和的平方变成三项和的平方,即

学生知道这个公式,在解决如(2a-b+3c)2这类题目时就比较容易了.
(3)与其他公式综合运用的总结:如计算(a+b-c)(a-b+c);(x-y)2(x+y)2.
(4)将a+b,a-b,a2+b2,ab看作整体进行运算的总结:如已知(x+y)2=9,(x-y)2=5,求xy的值.
将公式整理为 (a±b)2=a2+b2±2ab,(a+b)2-(a-b)2=4ab,根据已知条件选用不同的公式,就很容易求出答案了.
(5)逆向运用公式的总结:如计算(2a+b)2-2(2a+b)(a-2b)+(a-2b)2.
(6)配成完全平方式的总结:如已知x2+y2-2x+4y+5=0,求x,y;又如若x2+16x+k是完全平方式,求k的值.
在对知识进行总结时,要将知识和平时的练习相结合,这样才能使学生对知识的理解更具体,更深刻.
四、结论和反思
以上探究,经过日常教学实践,取得较好效果,特别是中等水平学生进步明显,这部分学生数学运算水平有较大提高,并逐渐养成良好的运算习惯,运算信心得到提升.但是因为数学运算具有系统性特点,对于运算知识掌握不系统、不熟练的中下水平学生,会因为以前运算方面存在的问题而影响现在的运算正确率.
学生在数学运算能力方面的不同表现,反映了学生不同的数学水平,学生在数学水平上的差异,给我们的教学带来一定的困难,因此在注重以上提出的方法之外,对不同运算水平的学生给予不同的要求,经常鼓励学生,耐心等待学生的成长,学生的数学运算素养必定会越来越好 .

