基于排队论的烟叶卸车服务台数量设置的建模与分析

梁 嘉，杨玉才，张万全，盛小贺

（红云红河烟草（集团）有限责任公司 曲靖卷烟厂，云南 曲靖 655000）

1 引言

原烟交接通常是卷烟收储最为忙碌的环节之一，原烟交接包含了车辆报到、烟叶卸车、取样分析、信息跟踪等多个环节。而目前国内复烤厂多采用人工卸车，不仅存在效率低下、安全隐患大的问题，而且用工成本逐年攀升，给复烤企业带来了较重的经济负担。除此之外，由于传统卸车服务台设置的不尽合理，造成烟车排队时间过长，从复烤厂的角度来看，增大了其管理成本，从货车司机的角度来看，降低了其货车的利用率，从各级收烟点的角度来看，加大了其库存压力。

排队论在很多行业都已经得到了非常普遍的应用，比如银行的排队智能服务系统，通过优化的窗口及排队设置，可以有效减少顾客等候时间及服务不满发生的流失率[1]；比如通信系统，优化的路由及硬件设置可以解决通信拥塞问题，提高信息传送质量及效率[2]；比如物流系统，通过合理的服务台数量设置、路线规划及跟踪优化，可以大幅提高物流运送效率，节约成本[3]。本文将依托烟叶卸车装框系统及收储管理平台，使用排队论建立排队模型，设置合理的排队系统以平衡资金投入及排队的效率。

2 排队论理论

排队论（queuing theory）又称随机服务系统理论，是通过对顾客到来及接受服务时间的统计分析及研究，得出顾客等待时间、顾客排队长度、系统繁忙程度等数量指标的相关规律，然后根据指标来改进服务系统的服务结构及模式，优化顾客的排队形式[4]。以此使排队服务系统既可以满足顾客对服务质量的需要，又能使服务机构的服务成本最低或能满足其他的要求，其系统排队模型如图1所示。

图1 系统排队模型框图

排队系统的三个基本组成：

（1）系统输入：顾客到达的规律；

（2）排队规则：顾客等待服务的排队规则；

（3）服务规则：服务台数量以及按照什么样的规则服务，顾客介绍服务的时间分布等。

3 烟叶卸车服务台模型建立

3.1 烟叶卸车服务台的工作模式

单台烟叶卸车服务台每次可为一辆货车提供卸烟装框服务，采用机械与人工结合的形式，每台烟叶卸车服务台1台剪叉电动式升降平台，升降平台上设置一台卸货链板输送机。升降平台可随卸货高度的变化自由调整高度，以适应人工搬运的需要。烟包卸车装框能力≥550包/h，基本配置为每个平台8人。

3.2 烟叶卸车服务台的建模

排队模型用X/Y/Z/A/B/C进行表示。第一个符号X表示顾客到达流或顾客到达间隔时间的分布：第二个符号Y表示服务时间的分布：第三个符号Z表示服务台数目；第四个符号A是系统容量限制；第五个符号B 是顾客源数目；第六个符号C 是服务规则，如先到先服务FCFS，后到先服务LCFS 等。并约定，如略去后三项，即指X/Y/Z/∞/∞/FCFS 的情形[5]。表示顾客到达间隔时间和服务时间的分布的约定符号为：M指指数分布，D指确定型；Ek-k指阶爱尔朗分布：G指一般服务时间的分布。例如，D/M/l 表示相继到达间隔时间为确定，服务时间为指数分布，单服务台的等待制系统。

针对复烤厂，将等待卸烟的货车定义为顾客，将烟叶卸车服务台定义为服务台。模型建立后主要目的为得出最优服务台设置数量，既能很好的满足客户需求，又能达到投资平衡点。经分析，可以将到达的顾客流看作是泊松分布[6]，服务时间即服从负指数分布。该系统即为典型的M/M/n排队模型，如图2所示。设系统有n 个服务台，各服务台工作相互独立；货车按泊松流到达，到达强度λ；各服务窗服务时间服从负指数分布，平均服务时间为1/μ，顾客在系统中的平均逗留时间为W，平均排队时间为Wq；系统中顾客数L，排队等待的顾客数为Lq；服务台空闲的概率为P0。

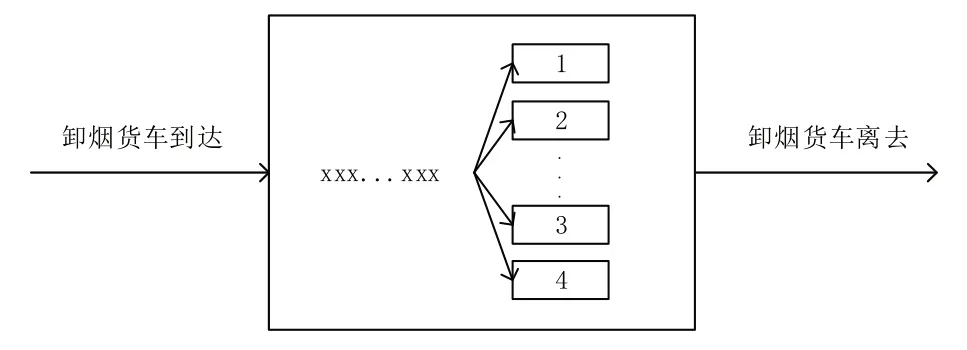
图2 M/M/n排队模型

对于n 个服务台的模型，ρ=λ/nμ 为衡量系统服务效率的重要标志，ρ 越小代表服务效率越高，服务质量越好，当ρ＞1 时，系统队列将无限长，代表该排队系统是无意义的。

因此，系统的平衡条件为ρ＜1。

M/M/n模型的系统运行指标为：

（1）平均排队等待队长：

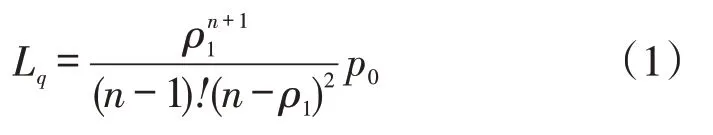
（2）平均正在服务的服务台个数：

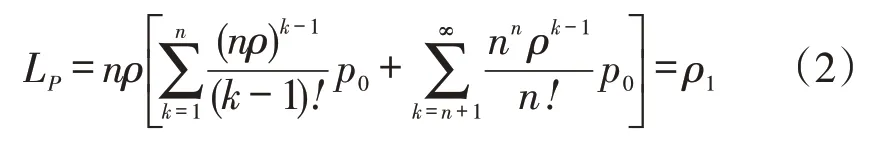
（3）系统内排队队长：

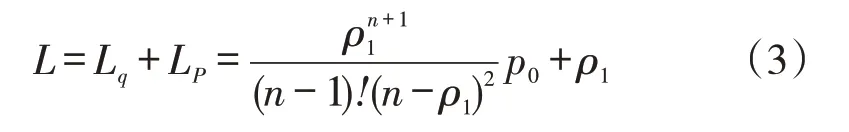
（4）顾客的平均排队等待时间：

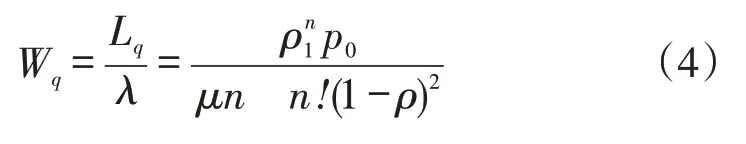
（5）顾客在系统中的平均逗留时间：

3.3 系统投资模型

每个服务台的一次性建设投资为T，单个烤季每个工人的用工支出为B，每个烟叶卸车服务台用工数为G1，以服务台设计使用寿命为S，投资平衡点时间为D，传统全人工卸车模式单个服务台所需用工数为G2，服务台建设数量为n1，目前复烤厂人工服务台数量为n2。整个模型需要同时满足以下2 个公式才具有意义，该系统才有投资价值。

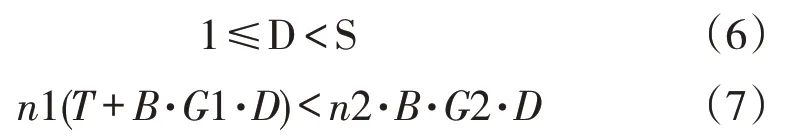
4 烟叶卸车服务台的模型验证及优化

4.1 系统参数

烟叶卸车服务台的设计稳定能力为550包/h，经统计，复烤厂在收烟季每天到达客户平均数量为40车，每车装载烟包600包左右。

复烤厂卸烟工作时间为上午8时至下午16时30分，每天客户到达时间区间为上午8时至下午15时，时长为7h。

客户到达强度在统计基础上稍留一定余量，则λ=6车/h；服务台的服务时间1/μ=1.1h/车。

烟叶卸车服务台建设投资T=100 万元/台，单个烤季每个工人的用工支出B=2 万元/人，每个烟叶卸车服务台用工数G1=8人/台，传统全人工卸车模式单个服务台所需用工数G2=18 人/台，目前复烤厂人工服务台数量为n2=9，服务台设计寿命S=15年。将各个参数代入式中得：

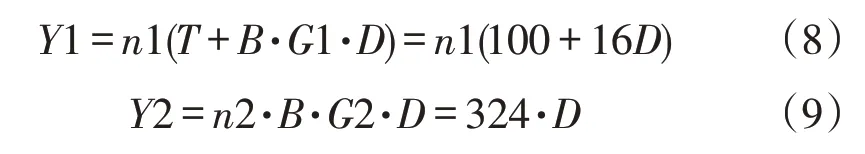
将式（8）、（9）代入式（6）、（7）得：

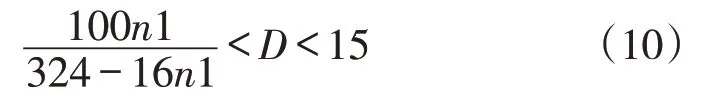
即n1 ≤13。

根据系统稳定条件ρ=λ/nμ＜1，将参数代入上式可以得出：n＞6.6，即服务台数量大于6.6台，且n为正整数，因此n≥7。综上，该模型存在的约束条件是服务台数量n 满足7≤n≤13。

4.2 模型计算及优化

将λ=5，1/μ=1.1，n 由7 至13 依次代入（1）至（5）的排队模型中进行计算，可以得到数据见表1。

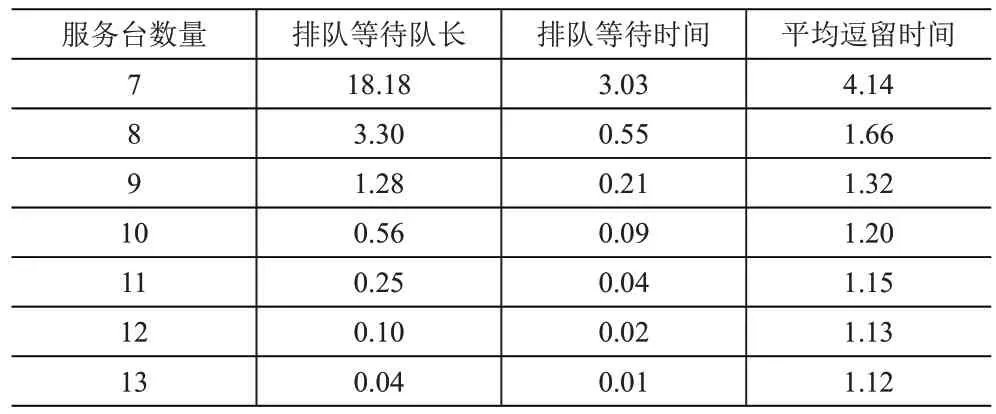
表1 不同数量服务台的顾客排队情况

为了更直观地进行分析，根据表1的数据绘制不同数量服务台的顾客排队队长折线图如图3所示，不同数量服务台的顾客排队时长折线图如图4所示。

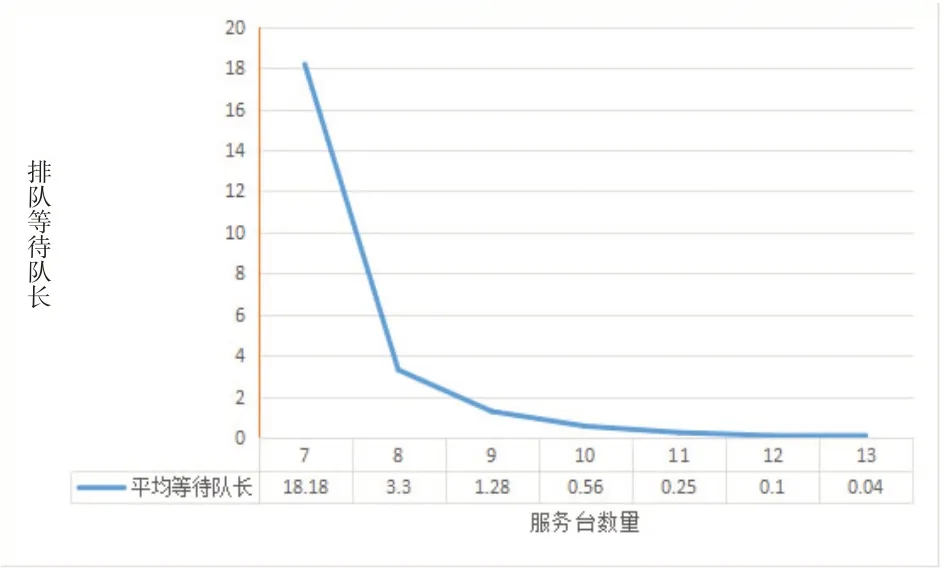
图3 不同数量服务台的顾客排队队长

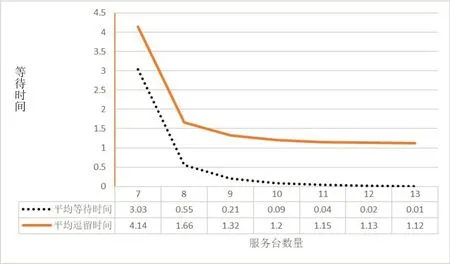
图4 不同数量服务台的顾客排队时长

根据模型结论，可以从图3、图4中直观的看出服务台数量为7 时，整个系统的服务质量较低，存在排队队长及排队时长较长的问题，显然会造成顾客的堆积。当服务台数量为8时，系统服务质量可以得到大幅改善，顾客在系统中的平均逗留时长为1.66h，若最后一位顾客为当天15时到达系统，而系统16时30分关闭服务，顾客能被完整服务的概率较小。当服务台数量为9 时，系统指标较好，顾客在系统中的排队等待时间为12.6min，逗留时长为1.32min，顾客等待时间可以接受，且能够得到完整服务的概率较大。因此，将服务台数量设置为9台是该烟叶卸车系统的最低要求。

在生产实际中，通常会为部分系统设置一定余量，以满足设备在故障情况下的正常生产。考虑该系统中留有1 台烟叶卸车服务台用于设备的故障备用、检修轮换，将服务台数量设置为10台即可满足要求，服务质量较9台更好。

设置10 台服务台，其在整个生命周期内的使用投入曲线如图5所示，对比原有的全人工卸车模式使用投入，在系统投入使用6年后，已达到投资平衡点，当15年生命周期满后，若以目前的人工成本计算，可节约资金约1 460万。

5 结论

通过使用排队论建模计算及优化分析，可以得出即能满足复烤厂卸烟能力要求，又能最节约投资的服务台数量设置。即使在收烟末尾客户流量较小的时期，也可以通过统计来量，对今后一定阶段的客户流进行预测，使用模型计算，相应的调整服务台使用数量，以达到节约人力成本，延长设备使用寿命的目的。该模型对物流排队新建系统具有很强的指导意义，针对不同的设计能力，通过计算甚至加上仿真实验验证，都可得到令人满意的效果。

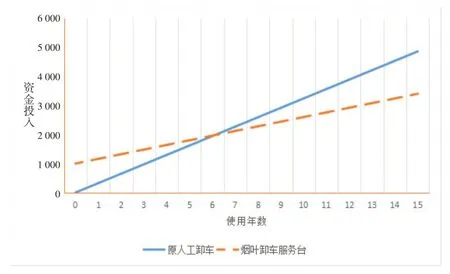
图5 原人工卸车及烟叶卸车服务台资金投入对比