一种多重构型约束条件下编队飞行卫星碰撞规避方法研究及应用

段 优，苏 鹏，高 燕，漆亚江，杨士其

(1.西安建筑科技大学，陕西 西安 710311； 2.西安卫星测控中心，陕西 西安 710043)

0 引言

随着我国在轨航天器数目的增加，在轨航天器之间以及在轨航天器和空间其他目标碎片发生碰撞的几率越来越大，其中低轨卫星发生碰撞的几率相比其他类型航天器更大[1]。目前，低轨卫星进行碰撞规避采取的普遍策略为：在碰撞预警时刻前12～24小时之间，对卫星进行升轨或者降轨控制，将卫星的轨道半长轴增加或者减小百米左右，使卫星飞行轨迹与目标星轨迹的最近距离保持在安全范围以内，从而起到规避碰撞风险的作用[2-4]。此类控制策略虽然规避效果良好，但仅适用于单独飞行、载荷独立使用的卫星。

对于以编队飞行的卫星星座，多星之间具有多重构型约束[5]，载荷也采用联合工作模式，当星座中某一颗卫星发生高碰撞风险事件时，若以常规碰撞规避策略对单颗卫星实时规避控制，将会使卫星星座迅速超出空间相对位置保持约束条件[6-7]，严重影响载荷协同工作效能，甚至导致载荷无法正常工作。而若同时对多颗卫星实时规避控制，虽然可以实现规避，但编队的重构会消耗大量卫星燃料，同时存在无法恢复至原有构型的风险。因此，研究在满足多重构型约束条件下，以单星小量半长轴控制方式，对编队飞行卫星实施碰撞规避具有重要意义。

本文针对编队飞行卫星碰撞问题，提出了一种在满足多重构型约束条件下，以单星小量半长轴控制方式对编队飞行卫星实施碰撞规避的方法。通过该方法，制定出以最小工程代价，同时保证载荷正常使用与卫星星体安全的控制策略。

1 编队飞行卫星星座构型约束条件

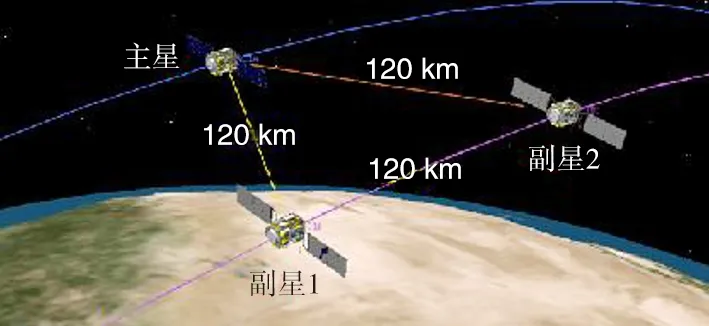
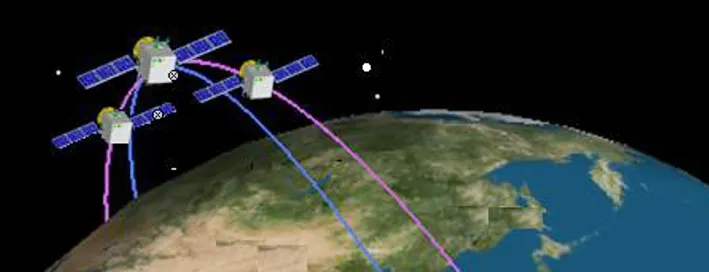
编队飞行卫星星座共包括N组卫星，每组卫星包括一颗主星(主星)和2颗副星(副星1、副星2)，其中副星1、副星2处于同一轨道平面内，主星所在轨道面与副星1、副星2轨道面仅升交点赤经存在小角度差。当每一组卫星的主星位于赤道正上空时，该组3颗卫星的标称位置构成边长为L公里的正三角形，副星1、副星2相对于主星具有组内构型保持约束要求，如图1所示；该编队飞行卫星星座中，各组卫星以运行于第一轨道面的F基为基准星，其他各组运行在多个轨道面内，每个轨道面平均分布2组卫星，F基与各组卫星在空间构成类walker星座，如图2所示。因此，每颗卫星在空间的位置，均受到组内、组间的多重相对位置保持约束限制，当卫星之间相对位置超出任何一种约束限制时，将使载荷协同工作效能急剧下降，甚至导致载荷无法正常工作。

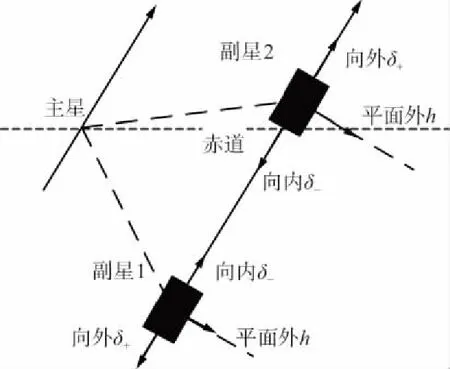
图1 副星1和副星2空间相对位置约束条件示意

图2 组间构型分布示意

1.1 组内构型约束条件

该编队飞行卫星星座每一组的三颗卫星以主星为基准，副星1、副星2相对于主星，具有轨道平面内向内、向外以及轨道平面外3个方向的空间相对位置约束条件，如图1所示。根据该编队飞行卫星星座天线设计特点及载荷工作原理限制，副星1、副星2在轨道平面内(δ)向内、向外以及轨道平面外(h)向内、向外最大漂移距离分别为-△、+4△、-6△和+3△，4个方向的约束构成一个矩形范围，称为控制盒。

1.2 组间构型约束条件

该编队飞行卫星星座每组可视为一个由三颗小卫星组成的虚拟分布式卫星，各组均以F基为基准，构成类walker星座，空间分布如图2示意。各组卫星所在轨道面，与基准轨道面之间保持△ΩN/2的标称升交点赤经差，并允许存在-Ωmax～+Ωmax的升交点赤经漂移偏差；在每一轨道面内的两组卫星相位相差180°，且允许在-△φmax～△φmax的范围内存在相位漂移偏差。

2 基于编队飞行星座构型保持的碰撞规避策略制定

根据航天器动力学相关特性[8-9]，近圆轨道卫星半长轴发生变化时，由于地球扁率J2项摄动影响，其轨道升交点赤经以及轨道平面内相位角(简称相位)也会发生变化。在对编队飞行卫星星座进行碰撞规避控制时，需要结合构型保持约束条件，在接近时刻之后，再次进行构型维持控制，以保证整体星座构型满足约束条件。因此，在选取编队飞行卫星星座碰撞规避控制量时，必须同时结合规避时刻前后星座构型以及两次控制最小间隔时间T(天)。

2.1 长轴变化对升交点赤经的影响

近圆轨道升交点赤经的漂移方程为：

式中，a为长半轴；e为偏心率；i为轨道倾角；n为卫星平均运动角速度；Re为地球半径。设标称轨道半长轴为a*，半长轴增量Δa，半长轴增量Δa导致升交点赤经漂移量为：

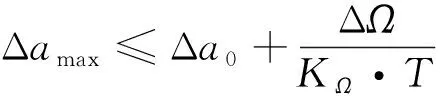
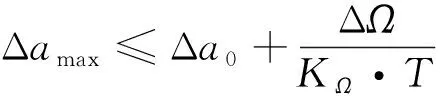
即：半长轴变化1 m时，每一天升交点赤经变化约KΩ度，称为相对升交点赤经变化率系数。以碰撞规避控制后T天内组间升交点赤经差约束仍满足要求为条件，最大控制量Δamax的范围为：

式中，△Ω为距离边界的升交点赤经差；△a0为目标星与基准星之间的轨道半长轴差。

2.2 半长轴变化对相位的影响

两组患者术后均有并发症发生，其中观察组患者的术后并发症发生率低于对照组患者，数据比较差异有统计学意义（P＜0.05）。 见表 2。

当卫星轨道半长轴发生变化时，相位漂移率控制方程为：

因此，轨道半长轴变化引起的相位漂移率方程为：

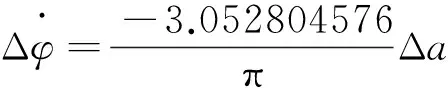
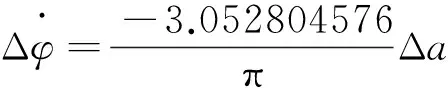
即：半长轴变化1 m时，每一天相位变化约Kφ度，称为相对相位变化率系数。以碰撞规避控制后T天内组间相位差约束仍满足要求为条件，最大控制量Δamax的范围为：

式中，△φ为距离边界的相位差。

2.3 组内平面外方向约束下的控制量选取

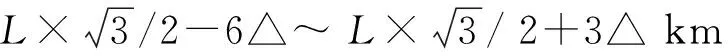
图3 组内平面外方向距离算法示意

由于星座组内平面外方向构型约束条件要求，当使三星中某颗卫星的半长轴变化Δa时，应满足：

Δa·KΩ(弧)·T·(ax+Δa)·sinix≤Δh，

式中，KΩ(弧)=2.0953*10-8为按弧度值计算的相对升交点赤经变化率系数；ax为轨控目标星X的半长轴(X代表主星、副星1、副星2中的一颗)；ix为轨控目标星X的轨道倾角(按角度值计算)；△h为当前目标星位置到平面外方向构型控制盒边界的距离值。对于该编队飞行卫星星座，轨控引起的半长轴变化量Δa远小于轨道半长轴ax，则在组内平面外方向构型约束下，以碰撞规避控制后T天以内构型不超差为条件，最大控制量Δamax的范围为：

2.4 组内平面内方向约束下的控制量选取

在轨运行时，该编队飞行卫星星座每一组内三颗卫星相对位置并不是完全保持不变。在每一圈的飞行轨迹中，当主星由南向北经过赤道上空时，三星呈正三角形构型(主星在副星1、副星2左侧，即图4(c)中A点位置)，此时主副星之间星间距离处于最大值，如图4(a)所示；随纬度升高，主星逐渐向副星1、副星2靠近；当达到最高纬度时按三星按副星2、主星、副星1顺序构成一条直线(主星位于图4(c)A'点位置)，此时主副星之间星间距离处于最小值，如图4(b)所示；随纬度减小，主星开始远离副星1、副星2；当主星由北向南经过赤道上空时，三星再次呈正三角形构型(主星在副星1、副星2右侧，即图4(c)中A"点位置)。

(a)主副星间距最大

(b)主副星间距最小

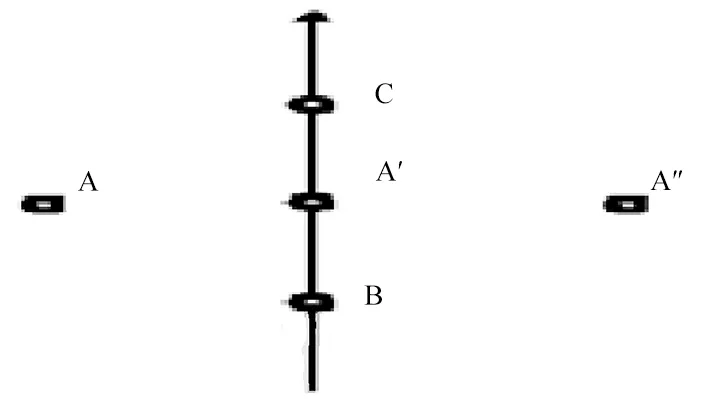
(c)主副星示意图4 某编队飞行卫星星座三星相对位置变化示意图

由于该编队飞行卫星星座每一组内主副星之间具备星间链路，可相互传送GPS定位信息，因此可直接计算出主副星间距离。相对于传统定轨数据，通过主副星之间星间距离数据确定三星相对位置，具有精度高、实时性强等特点。因此在轨运行期间，主要使用主副星星间距离数据最小值(星间最小距离)来确定该编队飞行卫星星座组内平面内方向构型。即：在标称位置处，主星至副星1与主星至副星2之间最小距离均应为L/2 km，在组内平面内方向构型约束下，星间最小距离应保持在L/2-△ km～L/2+4△ km之间。

因此，对于该编队飞行卫星星座，当某一颗卫星轨道半长轴变化1 m时，每天相对于自身标称位置(或同一轨道面内两星之间相对位置)变化约Kam，称为相对半长轴变化系数。则在组内平面内方向构型约束下，以碰撞规避控制后T天内构型不超差为条件，最大控制量Δamax的范围为：

式中，△S为当前目标星位置到平面内方向构型控制盒边界的距离值。

综上所述，在对该编队飞行卫星星座中的某一颗卫星制定碰撞规避策略时，除了要考虑卫星自身与碰撞目标之间的位置关系和轨道特征外，还需要结合组内、组间多重构型约束条件，计算在每一种约束条件下的最大控制量，选取满足所有约束条件的半长轴控制范围实施规避控制，才能在保证载荷正常使用情况下完成碰撞规避[10-12]。

3 方法应用

根据测算，2017年7月××日××时××分××秒，该编队飞行卫星星座F1组主星与某空间非合作目标红色预警级别碰撞风险，由于该空间目标为航天器碎片，不具备轨控能力，因此需要通过对该编队飞行卫星星座实施轨道控制来实现碰撞规避。此次碰撞规避控制是我国低轨编队飞行卫星进行的首次碰撞规避，在综合考虑保证载荷使用效能与满足星座组网构型多重约束条件的情况下，确定了以小量半长轴控制方式，仅对F1组主星实施轨道控制的碰撞规避策略。

根据前文分析得出的最大控制量选取策略，结合该编队飞行卫星星座F1三星以及F基最新轨道参数及星间距离遥测数据，按规避控制3天后进行构型维持控制为时限条件，即T取3天，计算出各种约束条件下最大控制量的选择范围如表1所示。

表1 各种约束条件下的最大控制量选取范围

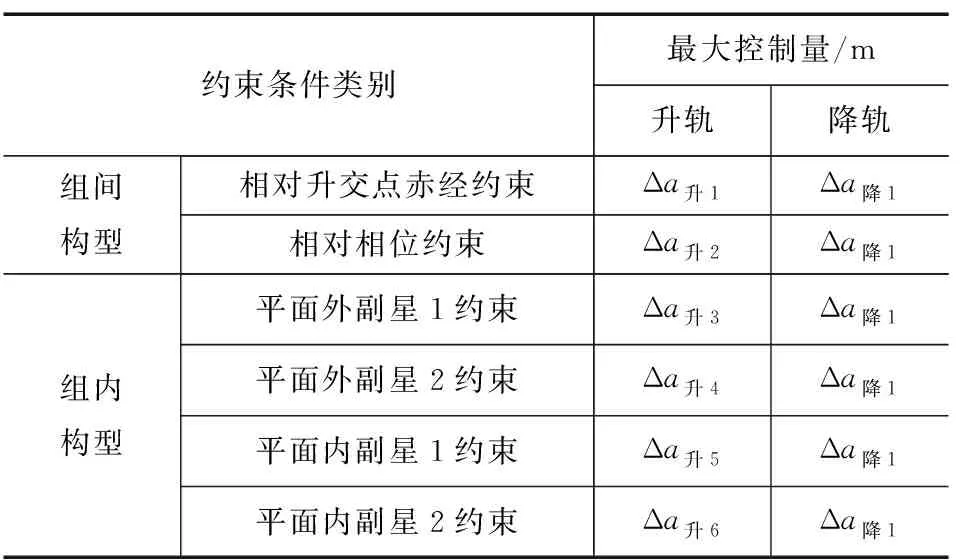
约束条件类别最大控制量/m升轨降轨组间构型相对升交点赤经约束Δa升1Δa降1相对相位约束Δa升2Δa降1组内构型平面外副星1约束Δa升3Δa降1平面外副星2约束Δa升4Δa降1平面内副星1约束Δa升5Δa降1平面内副星2约束Δa升6Δa降1

通过确定Δa升1～Δa升6之间的最小值与Δa降1～Δa降6之间的最小值，可以得出满足多重构型约束条件的最大升轨控制量和最大降轨控制量。最终，根据F1组主星与目标碎片的空间位置，确定出采用升轨控制的方案，选择于碰撞预警时刻前18小时，对F1组主星进行控制量为X m的升轨控制；并在碰撞预警时刻后12小时，对该星进行了计划控制量为Y m的降轨控制，用以进行构型维持。经过预警测算、精密定轨以及构型分析，采用上述策略实施的此次碰撞规避，在保证载荷使用效能未收到任何影响前提下，圆满的完成了碰撞规避任务，保证了卫星的安全。

4 结束语

编队飞行卫星星座包含卫星数量多，星座构型复杂，为保证以协同工作方式使用的载荷能够达到最佳使用效能，星座内卫星之间的相对位置具有多重严格约束。当星座中某一颗卫星发生高碰撞风险事件时，不论以常规的单星控制方式或者以多星同时控制的方式，均难以在满足保证载荷使用效能前提下，以较小的消耗和风险，完成碰撞规避。本文针对某低轨编队飞行卫星星座构型的多重约束条件，详细的研究了各类约束条件下，碰撞规避半长轴控制量的选取范围，提出了一种满足多重构型约束条件下，以单星小量半长轴控制方式，对编队飞行卫星实施碰撞规避的方法。并以2017年实施的我国首次低轨编队飞行卫星碰撞规避过程为例，验证了该方法的正确性。随着越来越多与该编队飞行卫星星座类似的卫星星座在轨运行，研究内容及结论对此类卫星的碰撞规避实施具有一定的借鉴价值。