LTE混合组网中基于多目标粒子群的自规划

董宏成，王腾云

(1.重庆邮电大学 通信与信息工程学院，重庆 400065； 2.重庆邮电大学 通信新技术应用研究中心，重庆 400065； 3.重庆信科设计有限公司，重庆 401121)

0 引言

随着移动通信网络的不断发展，频谱资源越来越稀缺，单制式基站独立组网由于容量限制，已无法适应网络需求，运营商为满足逐渐增长的吞吐量需求，合理地利用资源，在各地区逐步推进LTE混合组网[1]。LTE混合组网是将现有的高频TDD LTE与频率重耕的低频FDD LTE同时部署，异频的基站通过混合组网大大降低了同层之间的干扰，同时可以最大限度发挥每个系统的优势，弥补不足，降低投资成本，为用户提供高质量网络服务。LTE混合组网越来越受到关注，目前对其混合组网基站选址自规划要求变得越来越高。基站选址规划作为基站部署的重要参数，对网络的覆盖与容量有极大影响。现今移动通信网络复杂度越来越高，在很多场景下多制式基站并存，人工选址规划的方式很难找到最优解，同时运营商又要求缩减成本，提高规划效率，传统的以路测信息的人工网络规划方式难以适应需求，因此通信基站选址自规划显得尤为重要。基站选址自规划是通信网络自规划策略中的一种[2]，一般是选择最优站点位置以提升网络性能。近来有许多关于通信网络基站选址自规划的研究，文献[3]为降低TD-SCDMA基站网络建站代价，给出了一种基于免疫计算的基站选址优化方案。文献[4]在多基站协作通信场景下，构建了嵌套优化方案求得最小基站数目。文献[5]在宏基站和微基站异构网络下，从网络负载和网络能效2个方面进行多目标规划分析。文献[6]研究了LTE和WLAN融合组网中，用户接入自规划策略。此类自规划问题为NP难题[7]，目前多采用的智能优化算法主要有遗传算法[8]、模拟退火算法[9]、粒子群算法[10]以及其他改进的算法[11-13]。

综上所述，现有的网络自规划方法往往考虑目标不全，且改进的算法过于复杂，实用价值不高，无法适用于LTE混合组网下的网络自规划。LTE混合组网基站自规划与传统的基站组网自规划不同，规划FDD，TDD基站时需同时考虑多个目标，目前亟需研究LTE混合组网基站自规划，为运营商提供高效的基站部署方案。本文在以上研究结果的基础上，以覆盖率、负载率、能效比和成本为优化目标构建了LTE混合组网分层多目标基站规划模型，并根据粒子群算法使用范围广、收敛速度快的特点，使用改进的多目标粒子群算法优化模型。

1 LTE混合组网基站选址模型

1.1 问题描述

LTE混合组网自规划的一大特点是区域内存在2种制式的基站，FDD和TDD基站。其中FDD采用对称频谱，上下行传输由不同的频率承载，而TDD采用不对称频谱，上下行传输由不同时隙承载。在相同的单载波宽度条件下，TDD系统上行受限，覆盖范围明显小于FDD基站。在文献[14]已经指出LTE混合组网理想回传的部署方案，FDD作为宏基站，主要提供广覆盖，TDD作为小基站部署，主要吸收容量。由此在建模时应充分体现出LTE系统的优越性，建立双层网络，服务于热点区域和普通区域。

1.2 系统模型

无线网络规划的核心问题是在给定的区域内部署合理数量的基站，由于地理位置数量限制，能够安装基站的区域可能会出现无法安装或者已经安装基站的情况，因此在基站站址规划过程中，常常采用从候选站址集合中选取子集合的方法来规避该问题。现假设在给定的地域面积内，根据用户的数量和业务需求来设计一个最优网络规划，建模方法参考文献[15]。首先对所在地区进行业务预测，得到热点区域和普通区域，一个区域方块用方块中央测试点表示，该测试点的覆盖与容量情况就表示该区域方块的覆盖与容量情况。假设一共有N个测试点，N测试点又分为普通测试点N1个和热点区域测试点N2个。基站选址点为M个，TDD和FDD基站可共址建设，共有2层网络，k表示建设哪种网络。在M个候选子集上部署k层网络，每个基站都有2种选择，混合组网的基站选址矩阵为：

(1)

式中，akm为第k层m位置基站部署情况，“1”表示m位置上建设k层基站，“0”表示m位置上不建设k层基站。为体现LTE混合组网双连接的特点，测试点可以接入任意层网络，因此不必对测试点接入基站数量和类型做限制，只考虑是否满足测试点的业务速率，因此基站接入的指使函数为：

(2)

式中，Rmin，n为满足测试点n接入需求的最小速率，Rk，n，m为测试点n接收k层m位置处基站所能达到的业务速率，且热点测点的业务速率比普通测试点要求高。计算公式为：

Rk，n，m=Bk，n×lg(1+SINRk，n，m)，

(3)

式中，Bk，n为测试点n连接k层基站的带宽；SINRk，n，m为信噪比。测试点n的信噪比为：

(4)

(5)

(6)

式(4)中，Pk，m为k层m基站的发射功率；δ2为噪声功率。式(5)中，LOSSm，n为基站m到测试点n的路径损耗；(xn，yn)为测试点n的坐标；(xm，ym)为基站m的坐标；α为路径损耗系数，一般取大于2。式(6)中，In，m为测试点n接入到基站m后受到k层其他基站干扰。

由基站选择矩阵和测试点接入指示函数可得测试点最终接入基站选择矩阵H为：

(7)

覆盖率计算公式为：

(8)

网络能效比计算公式为：

(9)

网络负载计算公式为：

(10)

式中，

(11)

式中，Pth，m为基站m部署时应达到的负载阻塞门限，用于限制基站接入测试点接入数量[16]，仿真时取Pth，m=1。Ψk，n，m为基站m中的负载量占基站需求负载的百分比，实际工程中当此值超过门限Pth，m时，用负载限制因素exp(Pth，m-Ψk，n，m)来调节降低接入基站m的负载量。

自规划总成本计算公式为：

(12)

式中，Ck为第k层基站的成本单价。

综上所述，LTE混合组网的多目标自规划可以表达成如下模型：

(13)

2 求解算法描述

2.1 离散粒子群算法

基站自规划是一个多目标、多阶段、离散、非线性、受约束的混合整数规划问题[17]。离散粒子群算法是针对粒子群算法再网络规划中应用的一种改进[18]。离散粒子群算法采用二进制编码，粒子的每一维分量编码被限制为二进制1或0，对应每一层基站选址的状况，粒子速度的每一维分量是粒子位置分量编码选择0或1的概率，结合“V”型函数[19]，将粒子的速度映射到区间[0，1]上，更新后的速度和位置表示为：

(14)

(15)

(16)

(17)

式中，t为当前迭代的次数；tmax为最大的迭代次数；ωmax，ωmin分别为ω最大和最小的惯性权重，通常取ωmax=0.9，ωmin=0.4。

2.2 改进的多目标粒子群算法

求解离散多目标问题时，通常将Pareto排序机制和上述离散粒子群算法相结合，通过粒子间的支配关系确定粒子的历史最优解并更新非劣解集。本文根据粒子间的支配关系利用外部档案存储并输出Pareto最优解集，使用模糊决策方法选取最优的自规划方案(MDPSO/FD)。

多目标优化中，密集距离是对外部档案中每一个个体的度量指标，它表示个体与外部档案中相邻个体的拥挤程度，反映解集的完整性以及收敛性。粒子的密集距离具体计算公式为：

(18)

为提高Pareto解的多样性和均匀性，采用文献[18]中的循环删除方法进行非劣解集的更新，即按照式(18)拥挤距离排序后，去除密集距离最小的解，再计算剩余的Pareto解的密集距离，循环计算，直至剩余Pareto解的个数为预期设定的外部容量S。

在Pareto非劣解集中使用模糊决策方法，选出解集中粒子隶属度最大的最优折衷解。Pareto解集中粒子i的标准隶属度函数[20]ui表示为：

(19)

式中，

(20)

式(19)中，uij为第i个Pareto解的第j个目标值以及一般隶属度函数。

基于Pareto最优解的多目标离散粒子群算法的求解步骤如下：

① 输入数据。输入候选基站数目、测试点信息以及接入速率、函数边界和维度。

⑤ 根据式(14)～式(16)更新粒子的位置x和速度v，根据边界关系的值对位置x和速度v进行限定，并重新计算个体的适应度。

⑥ 更新外部档案。将进行位置更新后的粒子依次加入外部档案并判断支配关系。若新加入的个体支配外部档案中的个体，则加入该新个体并删除支配个体；若新个体不支配外部档案中的个体，则不加入；若无法比较，则比较当前外部容量S′和预期设定的外部容量S，若S′≤S，则新个体加入外部档案，S加1，当外部档案中的解大于规定值，使用上述循环删除方法进行非劣解集更新。

⑦ 更新粒子的Pbest。若满足最大迭代次数，则停止搜索，根据外部精英解集输出Pareto最优前沿，使用模糊决策方法[19-20]找到折衷解。否则t=t+1，转步骤④。

3 仿真结果分析

针对某电信分公司工程案例，对该城市密集市区进行理论化分析。该地区建设面积400 km2，根据现有流量业务预测判断，普通需求测试点N1有230个，热点需求测试点N2有220个，原有候选位置有70个。

仿真过程中设置网络负载最低门限Tload=2 000，种群规模P=100，算法最高迭代次数t=70次，外部文档最大容量S=100，图1展示了粒子迭代70次后初步自规划结果，总共选址得到基站数目为35个。大圆圈代表FDD基站，小圆圈代表TDD基站，加号点代表热点测试点，实心点代表普通测试点，图中显示热点区域基本被FDD和TDD基站覆盖，普通区域则基本被FDD覆盖到，说明本文提出的自规划方法初步具有可行性。

图1 基于MDPSO/FD的选址结果

为进一步验证提出的自规划方法可行性，将其与传统预规划中4个单目标最优规划进行分析对比，分别是混合组网中基站最大覆盖率(Max F)、最小网络能效比(Max E)、最大网络负载(Max L)和最小成本(Min C)。为验证本文改进算法的有效性，从上述4个方面将本文改进的算法(MDPSO/FD)与常规多目标离散粒子群算法(MDPSO)进行对比，得到2种算法在LTE混合组网自规划问题求解的性能对比图。

首先从最大化基站负载进行对比分析，为直观体现基站负载随粒子迭代次数的变化趋势，因此对基站负载数目进行归一化处理，对比结果如图2所示。

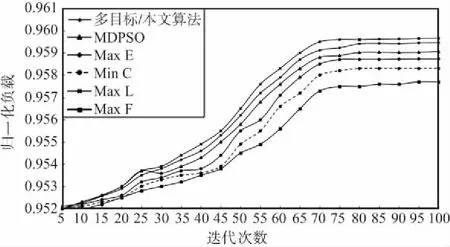
图2 网络归一化负载随迭代次数变化

由图2可以看出，归一化负载在粒子迭代到70次时趋于平缓，所以本文迭代次数取70。其中达到最高归一化负载的是最大网络负载的单目标模型，多目标模型优化的归一化负载迭代曲线与最大网络负载单目标模型保持一致，且始终高于最大化覆盖率单目标模型，最大网络能效比单目标模型，最小化成本单目标模型。MDPSO/FD算法随迭代次数递增达到归一化负载值始终大于MDPSO算法。

同样使用归一化能效作为参考，对各算法性能进行对比，对比结果如图3所示。

图3 网络归一化能效随迭代次数变化

图3展示了归一化能效随迭代次数的变化。迭代次数高于70时，归一化网络能效曲线趋于平缓。其中达到最高归一化网络能效比的是最大网络能效比的单目标模型，多目标模型优化的归一化能效比迭代曲线与最大网络能效比单目标模型保持一致，且始终高于最大化覆盖率单目标模型，最大网络负载单目标模型，最小化成本单目标模型。随迭代次数增加MDPSO算法达到的归一化负载值一直低于MDPSO/FD算法。

通过查询设备商报价，得到基站单价，FDD基站单价为38万元/个，TDD基站单价为42万元/个。在各算法下粒子迭代70次后，取覆盖率和成本进行对比，结果如表1所示。

表1 覆盖率以及成本比较

基站规划覆盖率/%成本/万元收敛代数(MDPSO/D)98.555070Max F99.185070 Max E92.680070 Max L93.285070Min C93.040070MDPSO97.060070

由表1可以看出，经过迭代70次后，多目标自规划模型的覆盖率低于最大化覆盖率单目标模型，且高于最小化能效比单目标模型、最大化负载单目标模型以及最小化成本单目标模型，同样经过MDPSO算法迭代的覆盖率略低于MDPSO/FD；另外，多目标自规划模型的成本低于最小化成本单目标模型，且高于最大化覆盖率单目标模型、最大化能效比单目标模型，以及最大化负载单目标模型。经过MDPSO/FD算法迭代后的成本低于MDPSO算法。上述对比结果表明，多目标自规划策略综合考虑到LTE混合组网的特性，尽可能地搜索到覆盖率高、成本低、负载多和能效比小的基站选址组合，具有一定的可行性。同时从4个方面将MDPSO/FD算法与MDPSO算法对比发现，MDPSO/FD算法在各方面都优于MDPSO算法。

4 结束语

LTE混合组网对基站自规划要求较高，本文结合混合组网策略，从4个方面改进了自规划方法。在自规划模型上，从覆盖率、能耗比、负债率、成本等4个方面综合考入自规划效果，建立低复杂度模型。多目标自规划模型能够在成本以及网络能效较低的情况下保证基站覆盖更多的测试点，具有可行性。在优化求解方面，本文引入改进的多目标离散粒子群算法进行寻优，与传统算法MDPSO进行了对比，提出的算法在寻优结果上均较优，能够得到合理的基站建设方案。LTE混合组网是运营商移动宽带的重要演进方向，因此网络自规划越来越重要。在下一步工作中，应提高自规划效率，逐渐摆脱个人经验，建立更加适合当前网络规划系统。