自适应池化卷积神经网络马品种识别研究

米克热依·迪里夏提，张太红

(新疆农业大学 计算机与信息工程学院，新疆 乌鲁木齐 830001)

0 引 言

近年来，突出马品种多元化发展、丰富马产业文化内涵已成为现代马产业发展趋势之一。现代化马产业体系中信息的采集、个体档案的创建、执行方案的制定以及品种溯源等，都需要对马匹进行快速准确的品种识别[1]。马品种的分类和识别一般以头部形状、别征、毛色等外貌特征为主要依据。目前，对于马品种的识别和管理主要靠人工进行，人工识别不但费时费力、费资并效率低。与此同时一般的非专业人员识别时会容易搞混。随着机器视觉理论研究的深入，图像的智能识别与应用已成为人工智能领域的热点。图像识别与人工识别相比，其独到之处是省时省力、效率高，不但能在种群生活的时间内实现实时监测，还能在不依赖人类视觉的情况下，实现行为的量化。当前，在对目标物体进行识别和分类的过程中，深度学习算法具有很好的效果。深度神经网络算法相较于早期依赖于先验知识进行特征提取的算法具有更强的敏捷性和适用性，可以使训练样本满足不同的网络构建特征。特别是在自动学习和图像特征提取方向上，卷积神经网络(convolutional neural networks，CNN)这一重要的深度学习神经网络算法具备较大的优势，这一算法已被应用到了图像识别、搜索引擎等领域，并取得了重大突破[2]。

1 卷积神经网络

卷积神经网络(CNN)是为了处理二维数据而构造的多层次网络结构。采用卷积运算逐层提取图片不同层次的语义，再靠数据样本的训练拟合调节每层卷积核的参数，然后在无监督学习下完成分类特征的提取。特征映射层和特征提取层被看作是卷积神经网络特有的神经元层。特征映射层(卷积层)的每个神经元的输入与前一层局部相连，靠卷积核数对二维数据完成卷积操作，并添加偏置向，提取当前局部特征，二次特征提取和求局部敏感性是通过特征提取层(降采样层、池化层、取样层)完成的[3]。卷积层和池化层在卷积神经网络中是按先后顺序出现的，并依次完成特征提取的工作。通过连续取征，使神经网络在对输入样本进行识别时具备较高的特征学习能力。卷积层中的特征映射是选取前一网络层中特征像的各角度特征，使其拥有扭转、位移不变的特性[4]。得益于CNN的权值共享能力，因而在不同的平面间的映射可以理解为卷积的过程，计算公式如下:

(1)

其中，n表示网络层数；K表示卷积核；Mj表示一种输入特征图的组合方式；b表示所有输出特征图必须具备的偏置项[5]。需要特别注意的是，因为一个输出特征图可能关联一个或多个输入特征图，如果关联多个输入特征图时，这些输入特征图需要对应各自的卷积核。池化层的任务是在上一层相似特征互相叠加的基础上，完成第二次特征提取，从而达到降低隐含层空间分辨率的目的。其次，它主要作用于图片中不重叠的区域，神经元X的计算公式如下:

(2)

其中，down()函数是一种下采样函数，依据池化操作计算方式的区别分为平均池化和最大池化[6]。

由于卷积神经网络通过卷积、池化等操作获取的特征值来计算损失差，并且使用反向传播算法更新网络参数，再通过分类器分类并得出识别结果，因此可否提取有效的特征值对于识别率的提高至关重要。而池化算法决定亚采样的结果，通过对该特征提取过程进行优化，对于识别率的提高意义重大。

2 自适应池化

图像池化从属于特征提取的质量，而提取的图像特征对识别率有很大的影响，常见的平均池化和最大池化模型都属于经典池化模型[7]。在池化操作中，平均池化模型先是对池化域中的所有值求和取平均，再把平均后的值作为子采样的特征值；而最大池化模型是取池化域内元素值最大的，并把它作为子采样特征值。最大池化计算公式如下:

(3)

其中，Rij表示池化值；公式第一项表示在大小为a×a的池化域中取最大值，a表示池化边长；b表示偏置[8]。

由于最大值池化仅对池化域中的元素取最大值，因此并不总会获取到有效信息。如图1所示，在2×2的池化域中a3为最大值，在a1,a2未知的环境下，池化域的特征值用最大值代替时会影响图片特征提取的精确度，从而影响到后期的分类工作。

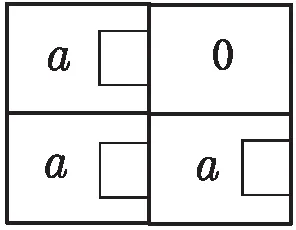
图1 最大池化域示意

针对马品种图像，由于其品种间差异大、图像背景丰富，再加上马体别征的多样性和马体姿势的多变性，使得经典的池化方法难以获取有用的特征值。为了最大限度提高模型的识别率，因此，在最大池化算法的基础上，用插值法建立数学模型并进行函数模拟[9]。其算法如下：

(4)

其中，μ表示池化因子，其原理是用μ改进最大池化算法。优化后的算法能够更精确地获取特征[10]。μ的计算公式如下：

(5)

其中，c表示池化域中除最大值之外元素的平均值；vmax表示池化域中的最大值；δ表示纠正误差项；θ表示特征系数[11]，计算公式如下：

(6)

其中，nepoch为训练次数，通过特征系数和池化域内各项值决定池化因子μ的值。池化因子在池化域大小已定以及迭代周期保持不变的情况下，是靠池化域的不同自适应取值；池化因子面临同一个池化域时，会根据迭代轮数的不同，动态调整并达到最优。池化因子μ∈(0，1)，这样既能在处理最大值特征明显的池化域时不失去精度，又能减小最大池化对其他池化域的影响，从而帮助卷积神经网络在不同次数的迭代下对不同池化域时可以获取到更加精准的特征，使自适应池化层提取到的特征值能够最大程度地反映原始输入图像。

卷积神经网络的卷积和池化过程都是在原始图像或者特征图像上经过从上到下、从左到右等滑窗操作实现的，因此可以用卷积完成自适应池化。由图2(a)所示，输入的特征像尺寸为3×3，卷积核尺寸为2×2，以步长为1进行卷积后的特征像尺寸为3×3，以步长为2进行池化后得到的特征像尺寸为2×2。由该过程可知，卷积结果相对于池化结果是从第2行第2列开始的偶数坐标值累加，而图2(b)表示，将卷积结果从第2行第2列开始的偶数坐标值进行删除操作即可得到池化结果[12]。

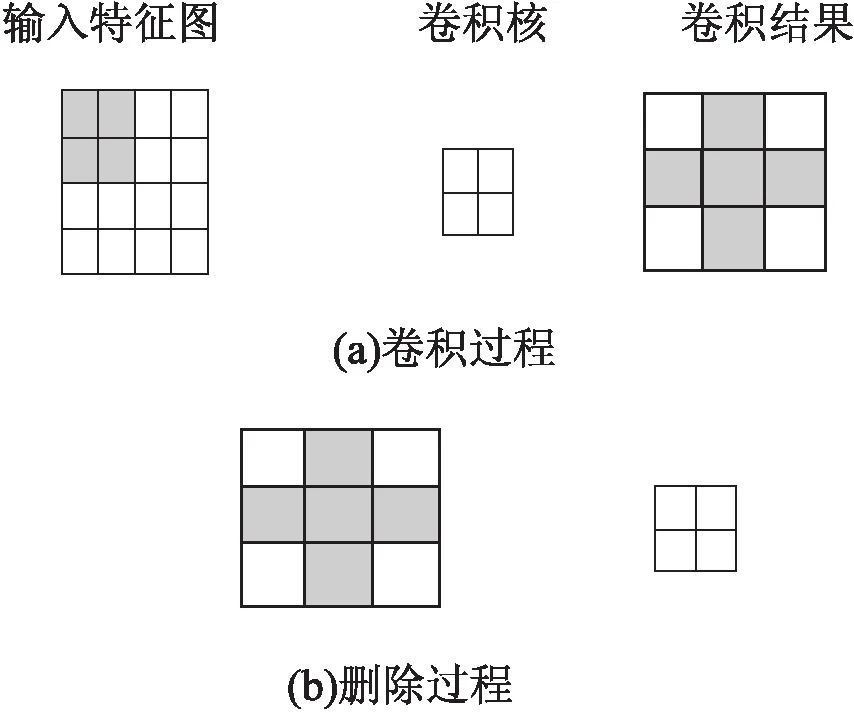
图2 卷积池化操作

图2(a)是大小为4×4的特征图，现有四个大小为2×2的卷积核分别为:

完成卷积计算后提取到4个大小为3×3的特征图，将其合并成4×3×3的多维矩阵，定义为T1，对该空间矩阵求取对应位置的最大值即可得到1×3×3的矩阵T2，对T2进行如上所述删除操作即可得到最大池化的结果[13]。

自适应池化是在卷积的基础上实现的，在得到T1后，在4个二维矩阵上进行对应位置的求和运算得到T3，再计算T3-T2，求剩余元素个数的平均值，即可得到式3中c的取值，根据式4以及c值即可求出池化因子μ值，由此可得自适应池化的结果。由自适应池化算法及实现过程可知，自适应池化是根据卷积与原经典池化的方式实现的，并未引进其他需要训练的变量，从而没有影响神经网络的反向传播算法更新参数的过程。

3 实验方法

3.1 数据预处理

3.1.1 数据集来源

文中数据集是由新疆伊宁市新源县马场和昭苏马场提供，部分数据是通过网络收集得来的。数据集中马品种图片都是RGB的、高分辨率的，其分辨率约为2 355×1 828像素。通过对拍摄和下载得到的图片进行研究和整理，将图像分成8个品种。如表1所示。

表1 自适应池化

3.1.2 图片归一化

在原始图像的采集过程中，由于图像来源于不同的拍摄设备，图像的尺度和焦点并不一致。由于卷积神经网络卷积过程对图像尺寸没有严格要求，因此输入图像经过卷积层后生成的特征图谱的大小会不一样，如果隐藏层直接与全连接层连接，则要训练的连接权值矩阵的大小会随输入图像的大小而改变，导致无法在同一个网络结构中用BP反向传播算法完成训练[14]。因此，将文中用到的所有马品种图像都归一化到224×224像素。为了保证缩放后的图像不失真，在缩放图像之前用resize-image函数对图像四边进行了一次判断，根据判断结果再通过增加黑色边框的方式把图像变成正方形，确保了图像的不失真。图3是吉普赛马图像缩放后的示例。

图3 图像归一化

3.1.3 数据扩增

通过深度学习进行图像分类时，需要具备足够的样本数据进行训练和验证，而当遇到样本数据量不足的情况时，必须通过数据扩增来弥补数据量不足的问题。对样本数据采用平移、旋转等方法，生成一定数量的子图像，由于这些图像是通过原图像产生的，也具备一定的可分类性[15]。除此之外，通过数据扩增可以解决一定程度上数据样本不均衡的问题。图4是阿克哈-塔克马(Akhal-Teke)用图像数据扩充后的案例，图4(a)为原图像，图4(b)是原图像经过水平移动、旋转、水平反转后获得的图像(M=10)。水平移动有利于改善特征定位在极小的面部挪动的条件下的鲁棒性；旋转使得模型可以学习适应复杂的姿势变化，从而解决了数据样本不平衡和少的问题。

图4 数据扩增

3.2 模型设计

文中模仿Alex Net网络框架，设计了11层的卷积网络结构，包括3个卷积层、3个池化层、2个dropout层和1个全连接层以及输入输出层。首先输入层的图像为224×224像素的RGB图像；卷积层conv1到conv3的卷积核数目分别是32、32、64，全部卷积核大小为5×5，对所有卷积都使用非线性激活函数ReLU，采用输入输出大小一致的方法把padding均设为1；池化层类型均为自适应池化(DA-pooling)，核大小均为2×2；Dropout层需确定一个参数表示舍弃激活层神经元值的比例，文中Dropout层舍弃比例分别为0.25、0.5，从而避免训练集复用造成的过拟合现象。为了便于理解，在图5中主要绘制了特征映射层、特征提取层和全连接层这三层网络。预处理图像后传入到网络中，主要通过特征映射层(卷积层、Conv)和特征提取层(自适应池化，DA-Pooling)交替叠加生成，全连接层(Fc)在Pool3之后。隐含层具备参数量少的优点，因为各层之间是通过局部相连和权值共享的方式建立连接。最后通过SoftMax函数对全连接层输出特征分类，并输出分类结果。

图5 Horse Net网络结构

4 实验结果与分析

4.1 实验设置

实验是通过Keras框架完成的。采用上文描述的CNN结构，通过输入规定格式的训练集样本数据进行参数训练，采用高斯分布作为网络初始权重的初始化方法，选取高斯分布标准差为0.01，均值为0。每次批量训练用8张图片。训练集中所有图片遍历一次看作是一次迭代(epoch)的过程，一共迭代1 000次。优化模型采用的是随机梯度下降优化算法(stochastic gradient descent，SGD)，算法动量因子设置为0.9。设置权重参数的初始学习速率为0.001。用“accuracy”方法评估模型性能,即为准确率。按照8∶1∶1比例在原始数据集上做分层取样，其中1 861个样本用于训练集，186个样本用于验证集，187个样本用于测试集。

4.2 池化层构建方法与数据扩增对实验结果的影响

不断使用验证集在训练过程中实时评测模型的预测性能，进而优化模型，将验证集预测的准确率最高的一轮训练结果选取为最终模型，并用于预测测试集数据。在上文为网络训练设置的参数不变的情况下，分别对使用最大池化、自适应池化以及数据扩增的卷积神经网络进行训练，并在测试集上测试模型准确率和误差。文中一共做了三组实验。实验一是在无数据扩增、无自适应池化的条件下搭建最初的网络并进行学习。由图6(a)可得，没有数据扩增、无自适应池化的网络在训练次数超过300后，验证集损失值(Validation Loss)开始不断上升，模型出现了较为严重的过拟合现象。这种严重的过拟合现象影响了模型的准确率，由表2第一行可见，模型在各数据集上的准确率较低、损失值偏高，测试集上的准确率也只有71.09%。为了改善模型，以实验一中搭建的卷积神经网络为基础，只在数据预处理中添加数据扩增一项，并再次学习；实验二训练结果由表2第二行可见。与实验一结果相比，用数据扩增学习后的模型测试集上的准确率比实验一高出9.59个百分点。由图6(b)和图6(a)相比，增加预处理项后的网络在一定程度上缓解了验证集损失值逐步上升的现象，但依然没有很好地解决模型过拟合以及准确率较低的问题。为了试着解决模型所遇到的颈瓶，在数据扩增的同时，对网络结构进行了改造，把原有的最大池化层替换成自适应池化层，并再度学习。由图6(c)和6(d)可得，用自适应池化学习后的模型验证集损失值与训练集保持同步下降、准确率则是保持同步上升，损失值最低达到0.46以下，准确率最高达到87%以上。由表2第三行可见，用自适应池化学习后的模型在各数据集上的准确率比前两次有明显的提高。而测试集上的准确率也达到了88.24%。

可见，自适应池化算法在避免模型出现过拟合现象的同时提高了模型的准确率，而且并没有消耗更多的时间。实验三模型的混淆矩阵如表3所示，模型的分类结果大都集中在混淆矩阵的对角线区域，表明模型具有一定的分类能力。其中模型对吉普赛马、哈福林格马、弗里西亚马的识别准确率较高，而对伊犁马、阿拉伯马的识别准确率较低。

表2 不同网络结构模型的准确率

图6 损失函数值变化曲线与准确率曲线 表3 模型分类结果

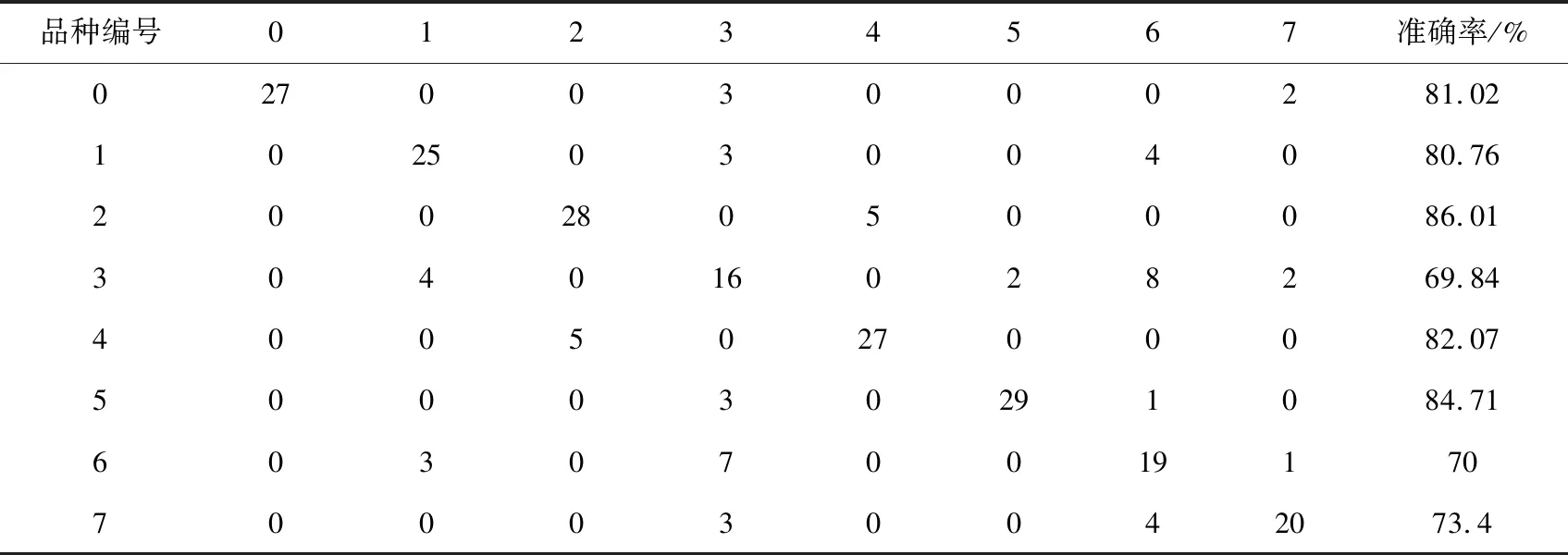
品种编号01234567准确率/%027003000281.02102503004080.76200280500086.01304016028269.84400502700082.07500030291084.71603070019170700030042073.4

5 结束语

文中提出了一种用于马品种识别的基于自适应池化的卷积神经网络模型。由实验结果可得，自适应池化算法在提高神经网络对马品种识别能力时效果最为明显，试着改善了网络拟合以及识别能力低的问题，改善了模型的收敛性和鲁棒性。与此同时，使模型拥有了不错的分类能力。由此可见，该自适应池化模型适合用于卷积神经网络处理二维图像的深度学习算法。