基于最优控制的船舶航向PID控制器设计

徐海东，刘刚，李家淦，周蓉

（山东交通学院船舶与轮机工程学院，山东威海，264209）

0 引言

随着航海业的迅速发展，海上交通密集现象不断增大，致使船舶航行的安全性和经济性等问题日趋凸显，因此，既有安全性又具有经济性的船舶运动控制方法成为业界重要的研究课题。近年来，在船舶航向控制上，发展出各种智能控制算法及各种混合控制算法，这些算法的控制效果较之PID 要好，但结构相比较为复杂，成品率较低[1]，这主要是由于理论到实践过程的滞后加之海上环境的严酷，而PID控制算法简单、可靠，技术比较成熟，促使现阶段船舶上仍会优先采用成熟的PID 控制器，致使智能控制目前还处于理论研究阶段，技术还不够成熟。

本文中为了保证航行过程中即能保持航向又能节省燃料资源，设计基于传统PID 控制算法设计线性二次最优控制器，根据船舶航行工况不同，将航向保持精度和燃料损耗进行折中处理，并在航行过程中改变航向，在模拟海浪干扰下，验证控制器的稳定性和鲁棒性。

1 船舶模型及海浪模型

在模拟航行仿真过程中，船舶运动的状态主要取决于船舶运动数学模型，船舶数学模型是对实际船舶系统的一种简化，并不代表实际的物理结构及全部系统信息[2]。在船舶运动控制领域主要是研究船舶操纵模拟器的设计及船舶航向保持系统仿真，根据研究对象不同选用不同的船舶运动数学模型，前者主要采用复杂的非线性数学模型，后者主要采用简单的线性数学模型。本文主要利用线性化数学模型来进行船舶航向控制器的仿真研究。

本文船舶运动模型采用野本谦作的Nomoto 模型。Nomoto 模型是由日本学者野本谦作在船舶运动线性方程的基础上，根据船舶运动推导出来的响应方程，其使用虽然有相对局限性，但在船舶运动控制仿真领域Nomoto 模型不失为一种较好的控制模型，能够得到较高的控制精度。

Nomoto 模型的两大优点：（1）在低频范围，其频谱与高阶模型的频谱非常接近；（2）设计出的控制器阶次低，易于实现[3]。

在知道船舶运动模型的8 个参数情况下，可以求得该船的K、T 参数，即可求出Nomoto 模型。

表1 船舶参数

“育鲲”轮T=62.38，K=0.31。Nomoto 模型为：

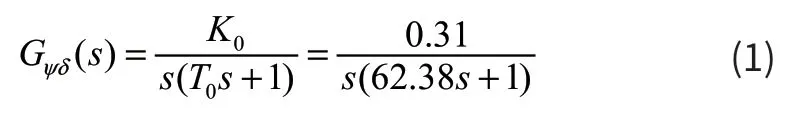
船舶在海上航行时，风浪是引起船舶偏航的主要原因之一，其中，海浪是影响船舶航行过程中最大的影响因素，主要体现在，在海浪的作用下，船舶会产生摇摆，从而造成航向偏差，因此在设计控制器时要考虑海浪的随机影响。实际海浪的主要特点为高度不规则性和较大的随机性，因此在仿真研究中通常将其处理为随机过程，本文中采用的是一种简单的成型的海浪模型，即利用白噪声驱动一个二阶典型环节模拟六级风引起的海浪干扰[4]。其传递函数：

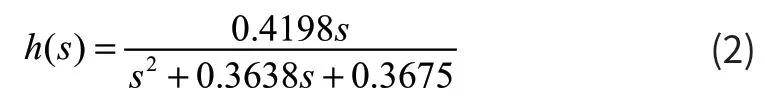
2 基于最优控制的船舶航向PID 控制器设计

PID 控制是应用最为广泛的一种调节方式，在模拟调节系统中技术最成熟，其结构简单，参数调整比较方便，适应性较强，是目前船舶航向控制中一直使用的比较成熟的控制规律，但单纯PID 控制作用规律对船舶航向控制在处理一些实际性问题时显得不够完善，因此，可以在PID 控制的基础上引入最优控制策略。

为了提高船舶航向保持精度，在燃料消耗最少的情况下，以最快的速度到达目标港口，要求整个航行过程始终处于最佳航行状态。由此提出一种自适应控制方案：最优控制。在这种控制中，要求控制器能够根据实际航向、航行环境及燃油燃料消耗情况而自动对舵机进行调节，使整个船舶随时处在最佳航行状态，这对航行的安全性和经济性有重要提升。

船舶在海上航行有两种工况：一是开阔海域，此时船舶以固定航速进行海上定速航行，动舵次数较少，因此主要是控制燃料消耗问题；二是狭窄水域，此时船舶动舵次数较多，来进行航线修正，因此主要是控制船舶航向控制的精准性。根据航行工况不同，将航向保持和燃料消耗进行折中处理，使系统处于最佳控制状态。

航向控制器的控制目标：

(1)在平静的海况下航向保持精度控制在0.50～1.00范围内，恶劣的海况下在航向保持精度控制在1.00～3.00范围内，具备抗干扰的能力。

(2)在船舶转向时，平静海况下航向超调小于5%,恶劣的海况下航向超调不应过大（不得＞30%）调节时间小于航迹引导的周期(30s～60s)。

(3)在整个航行过程中，动舵次数尽要少，幅度要小，以此减少舵机的机械磨损[5]。

控制原理如图1 所示。

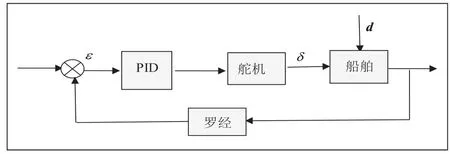
图1 船舶航向控制原理图

实际应用中，考虑到船舶航向保持和燃油燃料消耗两种情况，因此，提出以下性能指标：

其中，ε为航向偏差(ψrψ-),δ为舵角,d为外界干扰（风、浪、流等），λ为权值，根据工况不同选择不同权值。

控制规律型如：

关于权值λ的选取，实船试验表明，在有风浪干扰的海况下，主要是保证燃料消耗少，λ=8-10 时，能够达到比较满意的控制效果；在平静海况下，主要是进行航向的修正，λ=0.1 时，控制效果非常理想[4]。根据最优控制原理，得出式(4)中的各参数分别为：

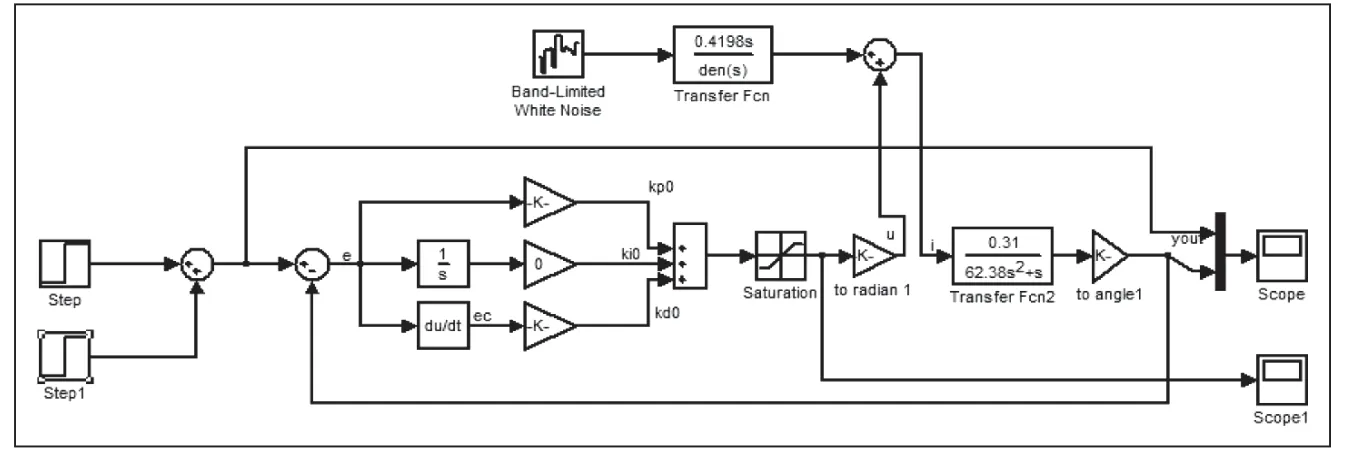
图2 仿真框图

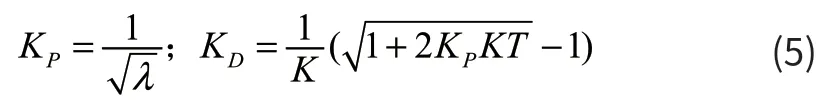
PID 控制表达式为：

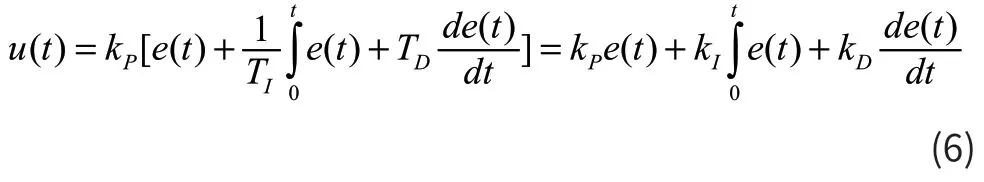
式中：u(t) 为控制器的输出信号；

kP为比例系数；

k I=k P/TI为积分系数；

kD=k PT D为微分系数。

将式5 带入到式6 中，便可得到最优控制PID 调节器。

3 算法仿真

本文借助MATLAB 仿真软件，在其Simulink 仿真环境中，以“育鲲轮”为被控对象，搭建仿真模型，如图2 所示，设置航向保持值40°，仿真时间1000s，并在500s 时进行转向，转向角度10°，仿真框图如图2 所示。

根据上文取λ=8时恶劣海况下，得KP=0.3536，，KD=9.1310.作为PID 控制作用规律参数值，仿真得出航向变化曲线和舵角变化曲线如图3 和图4 所示。

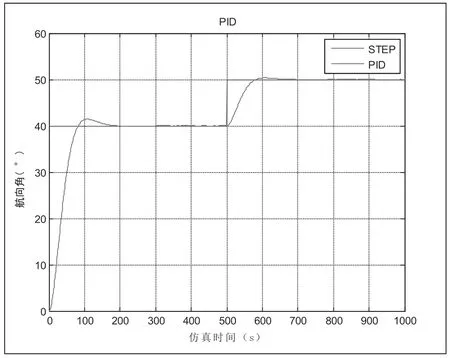
图3 航向输出变化曲线

4 结论

通过仿真曲线可以看出，在恶劣海况下，通过二次最优控制器仿真结果表明：在六级风的干扰下[5]，航向能够稳定在设定航向上，超调量符合要求，在500 秒时航向改变10°，控制器能够较快的控制转舵且动舵幅度不大（动舵死区限制在左右20°上），控制器的跟踪能力较强，超调量较小，稳定性较好，满足上述航向控制目标。此控制器可以作为智能控制算法研究基础。

图4 舵角输出变化曲线