基于锚定效应的估算和数感培养

郑金芳

[摘 要]估算和数感培养的受关注程度不断提升，基于锚定效应的估算和数感培养在小学数学教学中极为盛行。对锚定效应、学生的估算和数感开展基本分析，并结合实证，提出基于锚定效应的估算和数感培养策略。

[关键词]锚定效应;估算能力;数感

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2019）26-0042-03

对于小学生估算能力和数感的培养，教师可首先基于锚定效应培养学生的估算能力，由此学生可形成正确的数学观念，并对“数”产生更加直观准确的判断，进而提升数感。估算能力和数感的培养存在紧密的联系，值得教学一线的教师重点研究。

一、基本分析

1.锚定效应

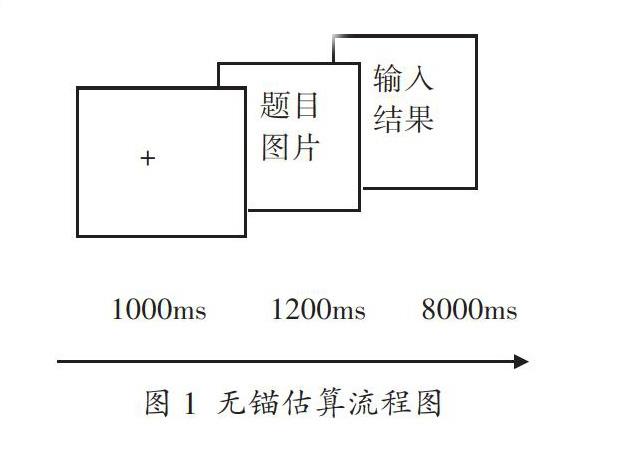
所谓锚定效应，指的是“人们需要对某个事件做定量估计时，会将某些特定数值作为起始值，起始值像锚一样制约着估计值，使估计值落于某一区域中”，如果“锚”定的方向有误，估计值便很容易出现偏差，这种偏差的出现很容易对学生的估算和数感培养造成负面影响。值得注意的是，锚定效应可细分为传统锚定效应和基本锚定效应，其中传统锚定效应包括比较问题和数量问题，两种问题的形式分别为“靶子的维度是高于还是低于某个锚定值”“靶子的维度是多少”;而基本锚定效应则源于“不把锚定值和靶子外显比较而仅仅提供数字而引起的锚定偏差”。为了明确锚定效应对估算和数感的影响，本文研究涉及的锚定效应包括传统锚定效应和基本锚定效应。

2.锚定效应与估算、数感的关系

锚定效应与估算、数感的关系属于国内外学界关注的焦点，如有关研究人员认为：“对领域知识的熟悉情况会影响锚定效应的发生，领域知识渊博的人不受或很少受到锚定值的影响，而专业领域知识较少的人较易受到锚定值的影响而得出更接近锚定值的估计结果。”将这一认知带入数学领域不难发现，数学估算能力较强的个体受到锚定值的影响较小，数学估算能力较弱的个体受到锚定值的影响则较大，而考虑到数感属于一种宽泛的基础性知识，且数感与估算能力二者之间存在一定影响，因此本文认为锚定效应对数感水平较高的个体的估算影响较小，而对数感水平较低的个体的估算影響则较大，由此即可更深入了解锚定效应与估算、数感的关系。

二、锚定效应对估算和数感培养的影响

1.实验对象

为明确锚定效应对估算和数感培养的影响，本文选择了笔者所在小学的235名四年级学生作为研究对象，并应用了李艳霞在《数感水平、锚定信息对小学生数学估计的影响》研究中提出的“小学四年级数感量表”进行学生数感测验，该量表由75道题目组成，答题时间为20分钟。根据结果将学生分为高数感水平组、中等数感水平组、低数感水平组（每组人数均为总数的1/3）。实验共收集数据200份，其中完整有效的数据155份。

2.实验设计

实验采用了3×3×3混合试验设计，数感水平为自变量，锚定效应包括传统锚定、基本锚定和无锚，估算的类型包括测量估算、计算估算、数量估算，组间变量为数感水平，组内变量包括估算类型和锚定条件，被试对象对各种估算任务的反应时和回答的正确率为实验因变量。

3.实验材料和仪器

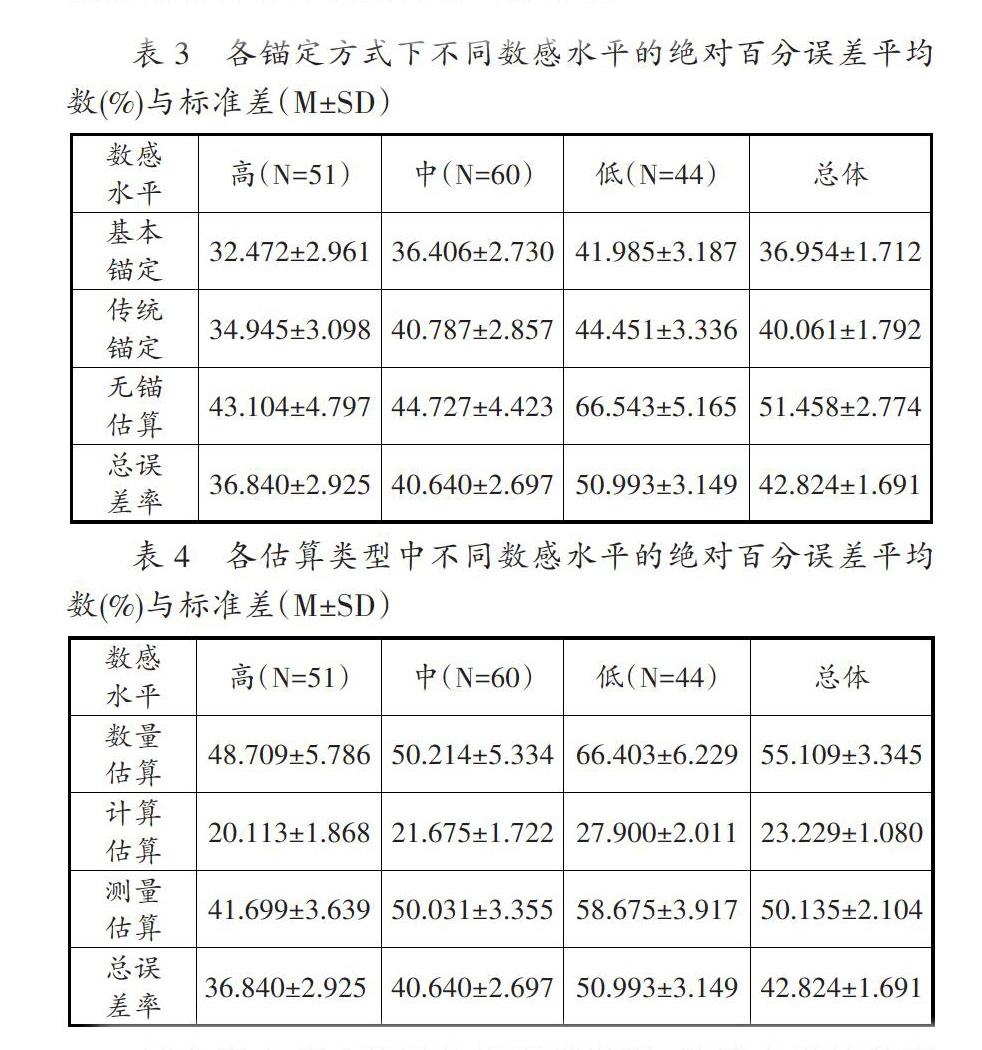
在估算题目的确定中，笔者结合国内外相关研究编制了初始的估算测验，并邀请教育专家进行审阅修改，最终确定了由测量估算、计算估算、数量估算各15道题组成的估算测验，估算测验的范围包括三位数加减法、长度90～250mm的线段、9～23个小方块;而在锚定值的设定中，笔者将确定的题目分成了同等的三部分，并为其中两部分题目设置了锚定值，其中传统锚定效应题目，如测量估算、计算估算、数量估算的锚定值距离精确值的绝对百分误差平均数分别为43.093%、11.185%、46.957%，总平均百分误差则为33.745%，基本锚定效应提出部分则分别为36.823%、15.526%、42.856%，总平均百分误差为31.735%;实验仪器为Windows7系统的计算机，且所有题目与答案输入界面均为白底黑色靶刺激的图片;数感测验采用了上面提到的“小学四年级数感量表”。

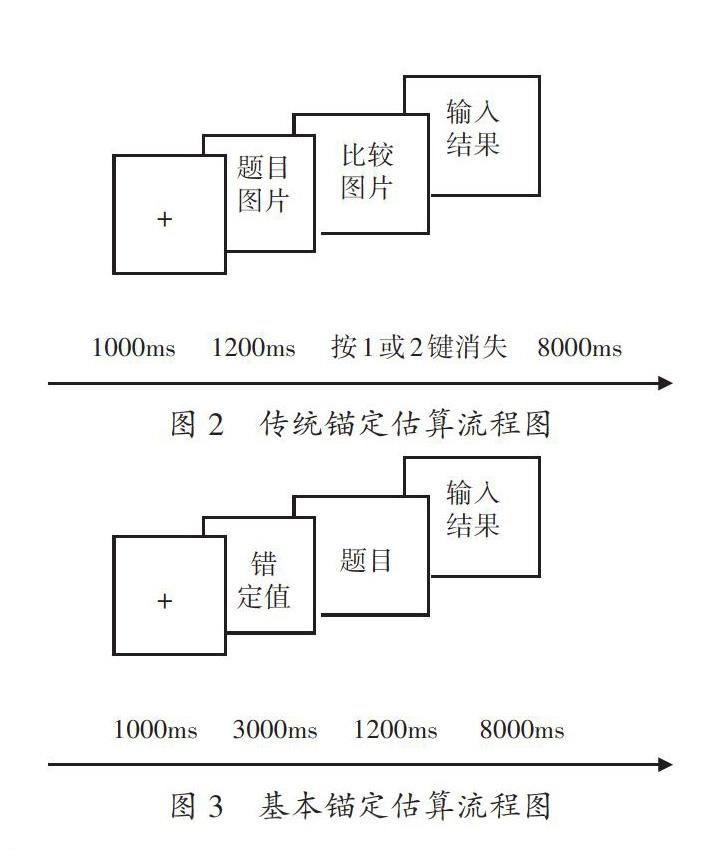
4.实验程序

7.深入探讨

深入分析可确定，被试数感水平越高，其反应时越短、正确率越高，但这种提高的差异并不明显;锚定信息对被试反应时和正确率的影响均较为显著，且锚定信息提高了估算的正确率;不同估算类型中计算估算的正确率最高，这与数学教学特点、小学四年级学生的技能掌握水平存在直接联系;锚定信息对三种数感水平的影响差距不大，但数感水平与锚定方式间存在交互作用，且锚定信息在一定程度上降低了各数感水平分组的百分误差。结合上述实验结果，可直观地发现锚定效应对估算和数感培养存在的显著影响。为了利用这种影响提高学生的估算能力，培养学生的数感，笔者结合自身的工作实践提出了基于锚定效应的估算能力和数感培养策略。

三、基于锚定效应的估算和数感培养策略

1.合理利用锚定效应

虽然实验证明了锚定效应可较好服务于学生估算能力和数感的培养，但实际教学中存在的锚定效应负面影响却使得很多教师不愿意利用锚定效应开展教学。如请一组学生回答问题：①泰国人口数超过4000万吗？②你猜泰国的人口有多少？再请另一组学生回答问题：①泰国人口数超过6000万吗？②你猜泰国的人口有多少？不难发现学生在回答问题二时均会受到问题一的影响，且问题二的答案随问题一中数字的变大而变大，这便是锚定效应负面影响的典型表现，因此基于锚定效应的估算和数感培养必须合理利用锚定效应。

2.合理使用估算情境

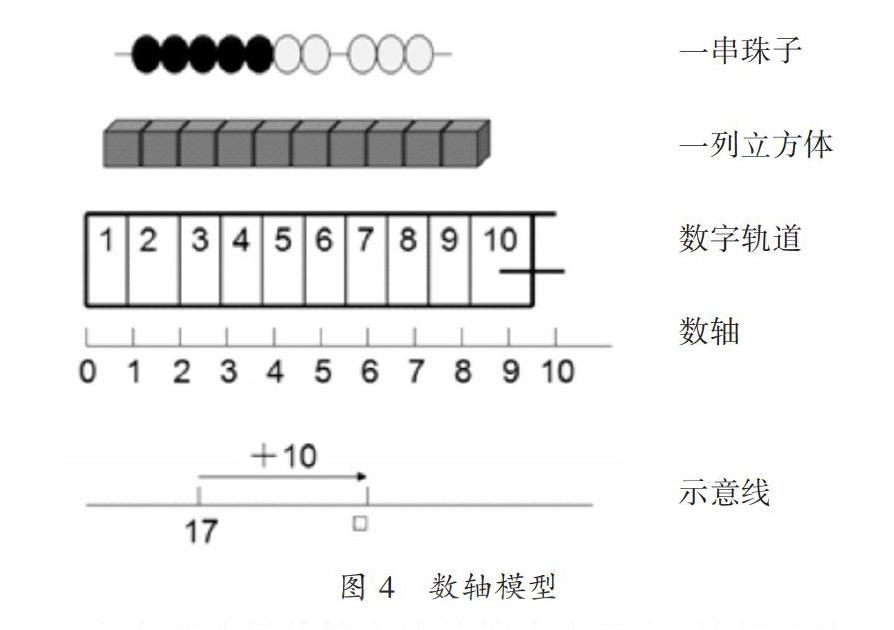
在利用錨定效应的同时，合理设置估算情境来培养学生数感也是很重要的，包括借助具体情境理解数的意义和估算价值、合理选择估算方法、数形结合理解估算等具体策略。其中，借助具体情境理解数的意义和估算价值可保证学生更加深入地理解数的内涵，并正视估算价值。如图4所示的数轴模型便能够保证学生在认识自然数之初深入理解数的内涵。为了使学生能够正视估算价值，教师则可以依据“有32人，每人买一份8元的小礼品”的购物情境，引导学生进行思考，并结合“应该带多少钱”“240元钱够不够用”等具体问题，使学生深入了解估算。

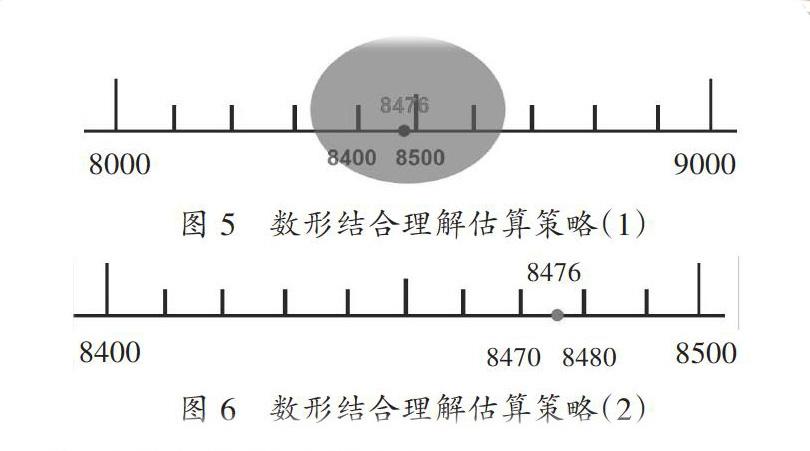
在合理选择估算方法的策略应用中，教师可基于 “242人去春游，每辆车可坐32人，共8辆车，够吗？” 这样的情境引导学生合理选择估算方法，并结合情境为学生提供“32×8≈30×8=240（元）”“32×8≈32×10=320（元）”“32×8≈30×10=300（元）”“32×8=256（元）”四种估算方法，学生便能够直观了解估小、估大、精算等情况下估算策略的应用价值，同时引导学生思考“一个因数小了2，一个因数大了2，为什么误差没有完全抵消？”，为学生的数感培养提供有力支持;而在利用数形结合理解估算策略的应用中，教师可基于图5、图6引导学生理解四舍五入，并应用相同的方法引导学生理解近似数，这同样能够为学生估算能力的提高和数感的培养提供有力支持。

3.应用多样化估算策略

学生的估算、数感培养还可以围绕多样化估算策略展开。具体来说，教师需认识到不同学生存在不同的思考方式和经验背景，由此引导、鼓励学生采用多种方法解决估算问题，使思维方式能够真正脱离传统教学的束缚。

数学教材提供了几种估算策略，且这些策略具备运用简单和差异性明显的特点，但教师在教学中不能局限于教材中涉及的估算策略，而应尊重学生的想法，鼓励学生采用不同的估算策略。例如，可通过“一本数学教科书有多厚”的问题引导学生采用“手测法”“目测法”等估算策略，也可以通过“学校操场面积有多大”的问题引导学生采用“经验法”进行估算，学生的数感、发散思维能力的培养都将由此得到有力支持。

4.重点关注思维过程

值得注意的是，估算意识薄弱、估算方法欠缺属于学生存在的普遍性问题，因此学生的估算、数感培养不能够仅停留在估算方法的教学层面，学生的思维过程同样属于教师关注的重点。为了真正提高学生的思维能力，教师必须通过实例让学生感悟到估算的价值和作用，并保证学生能够结合实际情况合理选择估算方法，通过亲身感受“进一法”“去尾法”“四舍五入”等估算方法的优势与不足，大幅提升学习估算的兴趣，由此真正实现愿意估算、主动估算、自觉估算、灵活估算。在学生估算能力不断提高的同时，数感自然也能够实现提升。

综上所述，锚定效应对估算和数感培养有较为深远的影响。合理利用锚定效应、合理使用估算情境、应用多样化估算策略、正确处理估算与精算的关系、重点关注学生思维过程等策略，为可行性较高的估算和数感培养提供了路径。为了更好地发挥锚定效应的正面作用，不可行锚的锚定效应也应成为教师关注的重点。

（责编 罗 艳）