考虑碰撞的冗余串联机器人冲击运动分析与优化

畅博彦 朱永杰 金国光 宋艳艳 李晓宁 路春辉

(1.天津工业大学机械工程学院， 天津 300387； 2.天津市现代机电装备技术重点实验室， 天津 300387)

0 引言

机器人在工作过程中，不可避免地与外界环境发生接触和碰撞[1-2]。碰撞会使机器人的运动状态和动力学特性发生变化，影响系统的正常运行，严重时甚至会使系统发生破坏[3-5]。因此，有必要在碰撞前对机器人的冲击运动进行分析和优化，以减小碰撞所产生的不利影响。

机器人系统碰撞动力学建模是对其进行冲击运动分析与优化的基础。RYU等[6]针对机械手工作过程中的碰撞情况，运用Lagrange方程建立了机械手的碰撞动力学模型，并用实验验证该模型的正确性；CHAPNIK等[7]考虑了多种阻尼效应，运用有限元法对单臂机器人碰撞动力学建模进行了研究，并模拟了机械臂在冲击载荷作用下的运动；金国光等[8]针对机械臂在运行过程中的接触碰撞问题，基于高斯最小约束原理和系统碰撞前的状态参数，提出了一种确定接触碰撞后系统状态量的分析方法；文献[9-10]针对柔性机器人碰撞时的动力学建模问题，引入冲量势，结合碰撞恢复系数方程，得到碰撞结束瞬时系统的广义速度求解方程；刘辛军等[11-12]对二自由度平面机器人进行研究，针对机器人的综合性能问题，提出了全域性能指标和局域性能指标的分析方法，以确定机器人的构件长度与性能指标之间的关系；贾庆轩等[13-14]根据空间机械臂在轨对接或装配时多重任务的要求，通过分析任务的特点，提出了多目标融合的冗余度空间机械臂碰前轨迹优化方法，并对机械臂碰前轨迹进行了优化；李宪华等[15]使用反变换法求解机械臂运动学逆解，通过给出解的组合原则，得到了该机械臂逆运动学的完整解析解，为机械臂的轨迹规划提供了理论依据；赵占芳等[16]针对冗余机器人的避障问题，根据雅可比矩阵的零空间，通过选取合理的放大系数，对串联机器人进行了运动学规划；温贻芳等[17]针对冗余机器人末端轨迹优化过程中关节空间运动稳定性不足的问题，提出一种以适应度函数为基础的关节空间轨迹优化算法；王安琪等[18]通过空间矢量引导、避障路径的比较，快速找到空间优化路径，实现多目标轨迹规划方法。以上研究工作为冗余机器人碰撞动力学建模和碰前轨迹优化提供了方法。

本文根据机器人的工作环境和使用工况的不同，将机器人的碰撞问题划分为无约束碰撞和有约束碰撞。无约束碰撞是指机器人在其工作空间内，不受环境和自身运动的约束，在任意位置均有可能触发的碰撞。有约束碰撞是指机器人在其工作空间内，受到环境或自身运动的约束而按特定条件触发的碰撞。针对两种碰撞类型，基于碰撞过程中的冲量原理与碰撞恢复系数方程，建立碰撞时系统所受外部冲量的求解模型。对于无约束碰撞，以速度突变量和冲量之间的映射矩阵为基础，从物理意义出发，构造冲击运动性能评价指标，研究冲击运动性能与机器人机构尺寸之间的关系，并绘制对应的局域和全域性能图谱。对于有约束碰撞，在冲击动力学模型的基础上，以系统所受外部冲量最小为目标，分别对定点碰撞和动点碰撞的碰前位姿进行优化，并进行仿真验证。

1 串联机器人系统外部冲量求解模型

在惯性坐标系中，假设机器人执行末端点坐标为Xact，相应的环境接触点坐标为Xenv，机器人的冲击运动如图1所示。

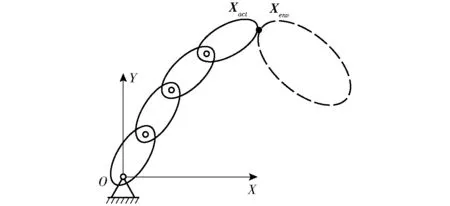
图1 机器人系统接触碰撞示意图Fig.1 Diagram of robot system with collision

针对n自由度串联机器人系统，记系统的广义坐标为q=(q1,q2,…,qn)T。根据Lagrange方程，其动力学方程可表示为

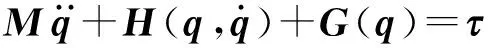
(1)

式中q——n×1维广义坐标向量

M——n×n维系统惯性矩阵

τ——n×1维广义坐标对应的驱动力矩向量

G(q)——n×1维重力对广义坐标的等效力向量

机器人机构的末端点在惯性坐标系中广义坐标的形式为

Xact=φ1(q)

(2)

在任意工作位置附近，令系统末端产生虚位移δXact，根据机器人机构的位置几何关系可知

δXact=Jδq

(3)

(4)

在系统发生碰撞时间间隔δt内，Xenv可以用广义坐标q表示为

Xenv=φ2(q)

(5)

当式(5)关系成立时，在接触点Xact处产生碰撞且外部冲击力为F，冲击力矩为τact。根据虚功原理，系统的主动力、主动力矩对作用点的虚位移作功之和为零，即

(6)

将式(3)代入式(6)可得

τact=JTF

(7)

当机器人末端受到外部冲击作用时，根据静力平衡条件，由式(1)和式(7)可知，机器人系统的动力学方程为

(8)

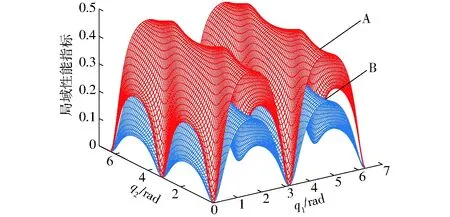
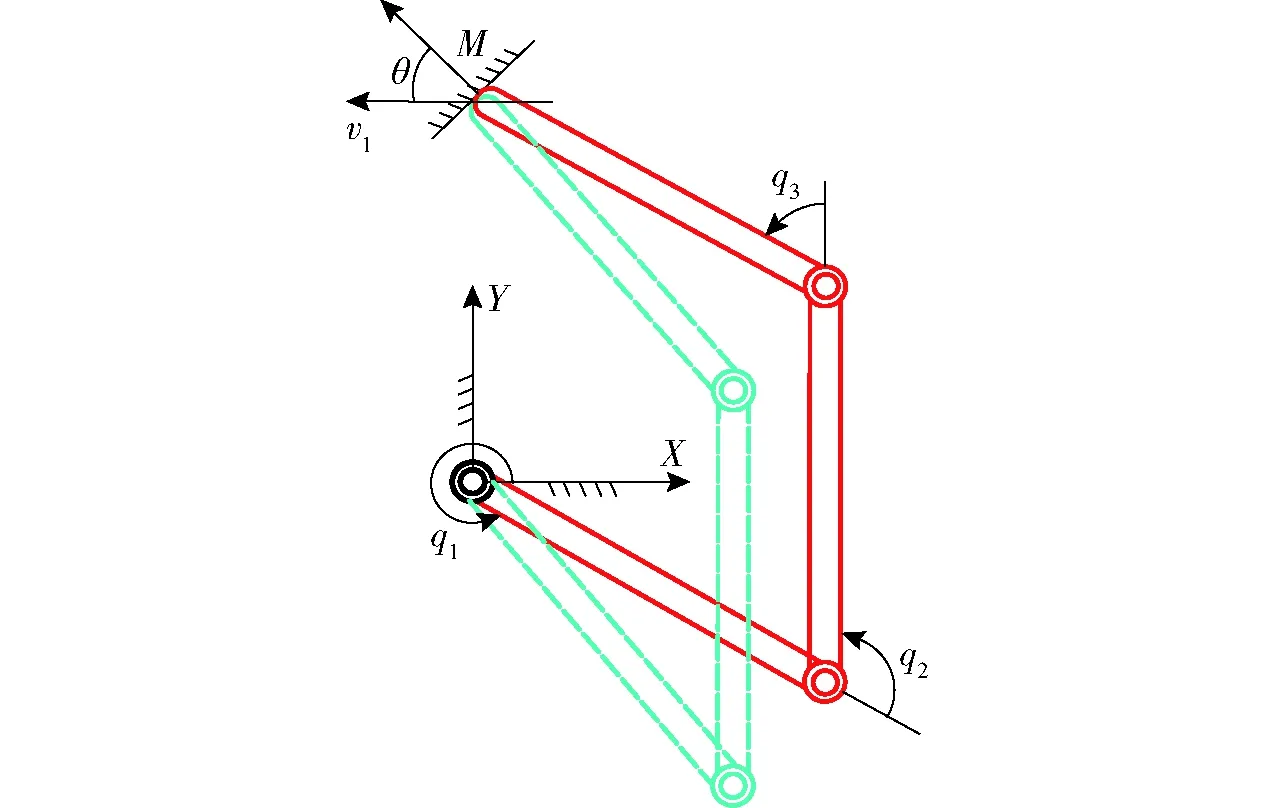
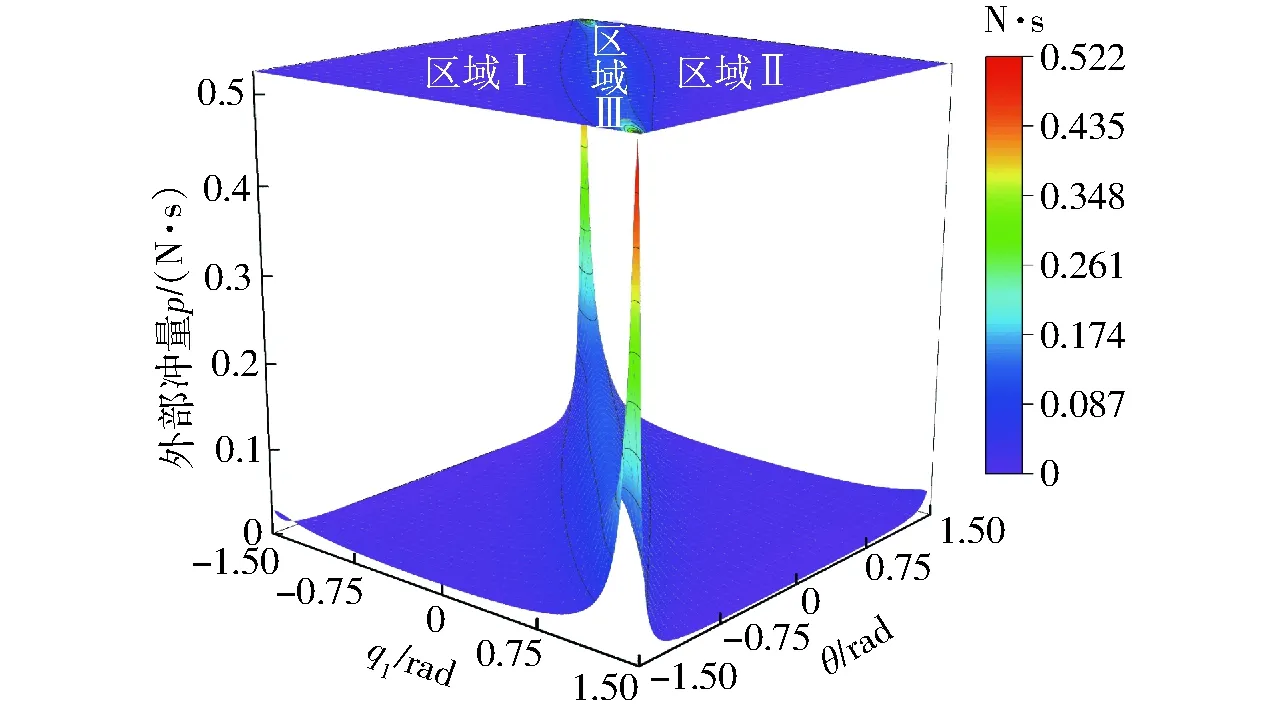
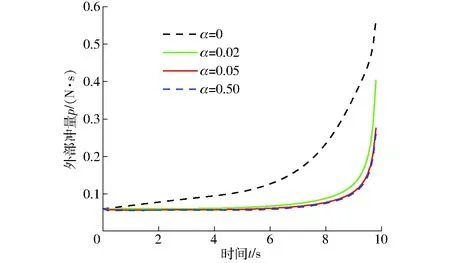
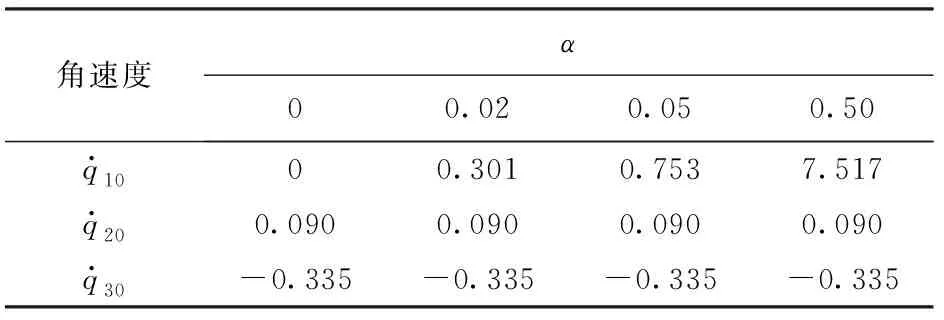
根据经典碰撞理论，对系统作如下假设：碰撞时间无限小，碰撞过程中所有杆的位置和方位不变，碰撞是点接触，碰撞过程中杆的形状和惯量不变[8]。由于碰撞过程多是弹性碰撞，设碰撞恢复系数为e(0

(δv1-δv2)Tn=-(1+e)(v1-v2)Tn

(9)

式中v1、v2——碰撞瞬时两物体在碰撞点的绝对速度

δv1、δv2——碰撞过程中的速度增量

根据上述假设可知，碰撞后机器人关节的位置保持不变，各关节的角速度是有限量。对式(8)在整个碰撞过程δt内积分得

(10)

式中t0——碰撞前的瞬时时刻

因为位移和速度在碰撞过程中为有限量，当δt→0时，式(10)左端的第2项趋于零，得

(11)

其中

式中p——碰撞冲量

由此可得系统广义速度增量的表达式为

(12)

碰撞点处的速度增量为

δv=JM-1JTp

(13)

假设机器人系统与外界环境发生碰撞，若碰撞时接触表面没有摩擦，则碰撞冲量的方向总是沿着接触点法向量n，将式(13)代入式(9)得

(14)

又因为

p=pn

(15)

则系统在碰撞点处所受到的冲量为

(16)

2 运动冗余串联机器人的无约束碰撞

2.1 冲击运动性能评价指标

机器人的冲击运动性能评价指标不仅与机器人的位形有关，而且与机器人的机构尺寸有关，机构尺寸参数的确定是机器人机构设计中的重要课题[19-21]。确定合理的机构参数是研究冗余串联机器人碰撞问题的首要条件，针对无约束碰撞时机构的稳定性分析，提出冲击运动全域性能指标和局域性能指标，可为机器人结构的设计提供依据。机器人发生碰撞时，外部冲量p与系统末端速度增量V之间的映射关系为

V=Jtp

(17)

其中

V=δvJt=JM-1JT

式中Jt——冲击运动映射矩阵，为对称阵

由于冲击力的不确定性，其计算值与理论值总会有一定的偏差δp，因此速度增量也会产生相应的偏差δV，即

(V+δV)=Jt(p+δp)

(18)

由式(17)和式(18)可得

δV=Jtδp

(19)

根据矩阵分析理论，可知

‖V‖=‖Jtp‖≤‖Jt‖‖p‖

(20)

(21)

‖δV‖=‖Jtδp‖≤‖Jt‖‖δp‖

(22)

(23)

式中‖‖表示向量或矩阵的范数。

由式(20)和式(23)可得

(24)

由式(21)和式(22)可得

(25)

由式(24)和式(25)可得

(26)

(27)

条件数kt是评价冲击运动映射矩阵病态程度的重要指标，可用来衡量冲击运动映射矩阵之逆矩阵的精确度，满足条件

kt≥1

(28)

由于机器人的冲击运动映射矩阵Jt是非常数矩阵，它与机器人的位姿、几何参数和物理参数有关。为了定量评价机器人的冲击运动性能，可在整个工作空间上定义其全域性能指标，即

(29)

式中W——机器人的可达工作空间

ηt——机器人发生碰撞时的冲击运动全域性能指标

由式(28)、(29)可知，全域性能指标ηt是一个大于零且小于或等于1的数。

全域性能指标是指每种具体尺寸机器人的性能指标分布在其整个工作空间内的平均值；与全域性能指标相对应，局域性能指标是指某一具体尺寸机器人机构的性能指标在其工作空间内每个形位的分布情况[21]。局域性能指标用ηJ表示。

(30)

用全域性能指标优化机器人机构时，优化结果为平均值最优，不能体现局域性能，还需要考虑性能指标值在具体工作空间内的分布是否合理。所以，在设计机器人机构时，需要综合分析全域性能指标和局域性能指标。

2.2 优化示例

图2的平面3自由度机构是串联机器人系统中最常见的构型，以该机构为研究对象，根据上述理论，研究各杆长度变化对机器人冲击运动性能指标的影响，以确定合理的机构设计参数。

图2 平面3自由度机器人Fig.2 Planar 3-DOF robot

当杆j(j=1,2,3)的长度为基准长度时，kij(i=1,2,3;i≠j)表示杆i与杆j长度的比值，为无量纲参数。由式(30)可分别计算并绘制出机构冲击运动全域性能指标随杆长的变化规律，如图3所示。

图3 机器人的全域性能图谱Fig.3 Atlases of global conditioning index for planar 3-DOF robot

当选择杆1长度为基准长度时，对应机器人机构的冲击运动全域性能图谱如图3a所示，指标值在图谱内的分布规律为：指标值与杆3长度成正比，与杆2长度成反比；由等高线的分布规律可以看出，杆2和杆3长度对指标值的影响程度都很明显。

当选择杆2长度为基准长度时，对应机器人机构的冲击运动全域性能图谱如图3b所示，指标值在图谱内的分布规律为：指标值与杆1长度成正比，与杆3长度成反比；由等高线的分布规律可以看出，杆1长度对指标值的影响程度都明显，当k12<1时，杆3长度对指标值的影响程度不明显，当k12>1时，杆3长度对指标值的影响程度逐渐增大。

当选择杆3长度为基准长度时，对应机器人机构的冲击运动全域性能图谱如图3c所示，指标值在图谱内的分布规律为：指标值与杆1和杆2长度成反比；由等高线的分布规律可以看出，杆1长度对指标值的影响程度明显，杆2长度对指标值的影响程度不明显。

在图3a中选取两组不同的杆长参数进行机构冲击运动局域性能分析，得到图谱如图4所示。其中，曲面A表示3个杆的长度l1=l2=l3=0.2 m时，机构的局域性能指标分布，曲面B表示3个杆的长度l1=l2=0.2 m、l3=0.05 m时，机构的局域性能指标分布。

图4 机器人的局域性能图谱Fig.4 Atlases of local conditioning index for planar 3-DOF robot

根据局域性能图谱可以看出，机器人的冲击运动性能与其位姿有直接关系，当机器人接近奇异位置时，其冲击运动局域性能指标显著降低，当机器人处于奇异位置时，ηJ=0，此时外部冲量的微小变化都会使得系统产生较大的速度波动。另外，由图4可以看出，曲面A所对应的机器人机构在外部冲击作用下保持运动稳定性的能力明显高于曲面B所对应的机器人机构。

3 运动冗余串联机器人的约束碰撞

令串联机器人机构的任务自由度为N1，机构自由度为N2，驱动构件数目为N3，当N1

根据碰撞时约束条件的不同，可对约束碰撞进行分类。当机器人末端与已知目标物在其可达工作空间内的某一定点以确定的运动速度发生碰撞时，称为定点碰撞，即定点碰撞的约束条件为机器人末端的位置约束；当机器人末端在其可达工作空间内沿任务轨迹运动的过程中，在某一瞬时与未知目标物发生碰撞，称为动点碰撞，即动点碰撞的约束条件为机器人末端的轨迹约束。

3.1 定点碰撞问题的优化

以碰撞时产生的外部冲量最小为优化目标，根据定点碰撞的定义，运动冗余串联机器人定点碰撞优化的实质是对碰撞时机器人机构的位姿和碰撞方向进行优化，根据式(2)、(5)、(16)可得其数学模型为

minp(q,θ)=

(31)

(32)

以平面3自由度串联机器人机构(图2)为研究对象，研究机构末端与固定目标物以不同的位姿和碰撞方向发生定点碰撞时所产生的外部冲量。在冲击运动全域性能指标分析的基础上，选取3个杆件的长度均为0.2 m。假设机器人机构末端沿X轴负方向以v1=1 m/s的速度在M点处与固定目标物发生定点碰撞，设定恢复系数e=0.8，θ为执行末端碰撞时的速度方向与接触点法线方向的夹角，q1、q2、q3为机器人机构的广义坐标，设置定点碰撞的约束条件为：Xact=Xenv=(0,0.2 m)，-π/2<θ<π/2，如图5所示。

图5 串联机器人定点碰撞示意图Fig.5 Diagram of serial robot’s immovable-point impact

将上述已知条件代入式(31)和式(32)可得机构发生定点碰撞时，机构位姿和碰撞方向对外部冲量的影响规律，如图6所示。

图6 外部冲量图谱Fig.6 Index of external impulse

由图6可以看出，定点碰撞时产生的外部冲量与机器人机构的位姿和碰撞方向紧密相关，在设计空间中的区域Ⅰ和区域Ⅱ，机器人机构发生定点碰撞时所产生的外部冲量较小，在区域Ⅲ所产生的外部冲量急剧增大，可根据实际工况的需求即尽可能避免冲击或利用冲击，进行相关参数的选取。

3.2 动点碰撞问题的优化

当机器人发生动点碰撞时，由于碰撞点未知，则需对其运动过程中任意时刻的位姿——动态位姿进行优化，使碰撞发生时产生的外部冲量最小。针对动点碰撞问题，首先运用梯度投影法得到考虑关节速度约束的运动冗余串联机器人的逆运动学解析解。

式(2)两边关于时间t求导得

(33)

(34)

式中J+——雅可比矩阵J的广义逆

I——单位矩阵

y——优化指标函数

式(34)右边第1项是方程(33)的特解，是机器人基本运动要求的最小范数解；第2项为齐次解，表示机器人关节空间的自运动。运用雅可比矩阵的零空间可以实现在不改变执行末端运动规律的情况下，对其关节角速度进行优化。

由式(16)可知，冗余串联机器人发生动点碰撞时，碰撞产生的冲量与式中的分母成反比，取冲击运动性能指标函数为

(35)

(36)

α——放大系数

可通过仿真法予以确定[16]。针对动点碰撞问题，通过优化μ值，即在运动过程中使其数值尽可能大，以达到减小外部碰撞冲量的目的。

以平面3自由度串联机器人机构(图2)为研究对象，对其进行动点碰撞问题研究。同样选取3个杆件的长度均为0.2 m，质量为0.1 kg。机器人各关节的初始状态为q1=-2π/3、q2=2π/3、q3=2π/3，如图7所示。

当串联机器人执行末端沿着向量n=(cos(π/4),sin(π/4))T方向，v=0.06 m/s作匀速直线运动时，对应μ如图8所示。由图8可以看出，α取正数时，μ随着α的增大而增大，当α>0.05时，μ值增大不明显，因此可在0～0.5之间选取合适的α值。此外，优化后机器人机构运动过程中的μ值明显大于优化前(α=0)，结合式(16)、(35)可知，优化后的串联机器人在运动过程中的任意时刻发生碰撞，所产生的外部冲量都可得到有效降低，优化效果明显，如图9所示。

图7 串联机器人动点碰撞示意图Fig.7 Diagram of serial robot’s movable-point impact

图8 性能指标函数Fig.8 Performance index function

图9 外部冲量Fig.9 External impulses

基于逆运动学解析解可求得机器人机构中各构件的运动轨迹，如图10所示。

图10 机器人运动轨迹图Fig.10 Diagrams of robot’s trajectory

对应α取不同值时，根据式(34)可求得各关节的初始广义角速度，如表1所示。

由表1可以看出，关节1的初始广义角速度随着放大系数α的增大而成比例增大，且数值变化较大，该结论也可从图10中得到验证，其余两关节的初始广义角速度不变。可以发现，如果α取较小值，发生碰撞时对机器人机构的外部冲量优化效果不明显，如果α取较大值，机器人机构关节空间自运动的速度有可能很高并引起关节速度越限。因此，需要综合分析机器人机构碰撞时外部冲量、运动轨迹及各关节的初始广义角速度，在计算仿真分析的基础上选取合理的放大系数。

表1 机器人关节初始广义角速度Tab.1 Initial generalized angular speed of robot joints rad/s

4 结论

(1)对运动冗余串联机器人的碰撞问题进行了分类研究，根据机器人操作环境和使用工况的不同，将其碰撞问题划分为无约束碰撞和有约束碰撞两大类，约束碰撞中由于约束条件的不同又分为定点碰撞和动点碰撞。

(2)将多体系统冲击动力学方程与碰撞恢复系数方程相结合，推导得机器人系统发生碰撞时的外部冲量求解模型，该模型中碰撞点的速度与碰撞冲量之间解耦，有利于计算求解。

(3)针对无约束碰撞问题，提出了冲击运动映射矩阵的概念，构造了机器人的冲击运动性能评价指标，该指标可用于评价系统在受到外部冲击作用下保持运动稳定性的能力。

(4)针对定点碰撞问题，结合碰撞时的位置约束条件，建立了系统发生碰撞时的优化设计数学模型。针对动点碰撞问题，运用梯度投影法建立了考虑关节速度约束的串联机器人逆运动学求解模型，该方法可使得机器人发生动点碰撞时产生的外部冲量最小。