基于细化法的土壤孔隙骨架提取算法研究

韩巧玲 赵 玥 赵燕东 潘贤君 彭 涌 郑一力

(1.北京林业大学工学院， 北京 100083； 2.城乡生态环境北京实验室， 北京 100083；3.林业装备与自动化国家林业局重点实验室， 北京 100083)

0 引言

土壤孔隙结构是土壤固相颗粒、土壤有机物、微生物等各相物质在空间排列后形成的空隙[1-3]。其几何形状、空间分布、连通性能等三维特征决定了养分运移能力、透气性等土壤功能，对于土壤生态过程具有重要影响。因此，对孔隙三维特征的描述和量化分析是研究土壤功能多样性的一个重要方向。

近年来，计算机断层扫描技术(Computer tomography, CT)在土壤领域的成功应用，能够实现土壤孔隙三维结构的可视化[4-5]。由于土壤组成成分的复杂性，使得孔隙结构具有多种几何形状和多尺度特征：①孔隙呈不规则的几何形状，并向多个方向发育延伸。②具有不同数量级的几何尺寸。③多尺度特征的孔隙相互交错。复杂的拓扑结构，使得土壤孔隙的研究难度大。为了探索复杂孔隙结构的体积、曲折度、连通性等特征，需要结合重构技术对其空间结构和拓扑特性进行分析，在这一过程中，孔隙骨架模型的构建方法至关重要。

现有的骨架化方法中，应用较多的主要有广义势场法、Vonoroi图法、Reeb图法、距离变换法和细化法。广义势场法的构建精度较高，但算法复杂度高，运行时间长，不利于实际应用[6]；Voronoi图和Reeb图是基于几何分析获取的骨架模型，适用于结构相对简单的几何图形[7-9]。应用范围最广泛的距离变换法和细化法易操作，精度高，适用于不规则的土壤孔隙，有利于保持孔隙骨架模型的中心性和连通性[10-11]。

本文将采用距离变换法和细化法构建土壤孔隙骨架模型，并结合土壤孔隙结构的特性增加细化法的限制条件。试验分别以自定义规则结构和土壤孔隙结构为应用对象，在连通性、细化性和中心性3个层面比较2种算法的构建效果，并通过对中心性的量化分析，证明细化法对土壤孔隙骨架模型构建的优越性，为从孔隙尺度理解土壤功能提供一种较为先进的技术手段。

1 土壤样本采集与图像预处理

1.1 土壤样本的采集

研究所用土壤样本采自黑龙江省克山农场(125°8′～125°37′E，48°12′～48°23′N)，该地区属于典型黑土区，年平均气温1.3℃左右，年降水量约502.5 mm，其土壤类型以黏化湿润均腐土为主[12]。于2017年10月初，采用自制的内径和高度分别为10 cm的圆柱形有机玻璃管于土壤深度为0～40 cm的侵蚀沟壁进行原状土取样。通过机械分层法，每10 cm取一次土样，每层重复取样3次，共得到12个土壤样本，以供后续CT扫描用。

1.2 土壤CT图像的获取

所用的土壤CT图像由黑龙江省中医药大学的Philips Brilliance 128排64层螺旋CT机扫描土壤样本获得。在土壤样本扫描前，为了保证土壤成像的精度，采用标准水膜对CT机进行校正。扫描过程的参数选择为：电压120 kV，电流196 mA，扫描层厚0.625 mm，窗宽和窗位分别为2 000和800[13]。经过螺旋扫描，每个土壤样本得到236幅土壤CT图像。

1.3 土壤CT图像的预处理

由于医疗CT机扫描土壤样本后得到的是包含256个灰度级的DICOM格式图像，不便于进行后续的图像处理操作，因此，为保证土壤CT图像的可操作性，将原始土壤CT图像存储为BMP格式。图1a所示为原始土壤CT图像，圆圈内为有效的土壤图像，为了减少算法占用内存和提高图像处理的执行效率，第1步需要对原始土壤CT图像进行剪裁处理。另外，考虑到土壤圆柱与PVC玻璃管边界处会存在一定晃动，可能会导致土壤边界存在一定畸变的情况，因此，本试验采用最大内切正方形的方法，将土壤CT图像剪裁成尺寸为289像素×289像素的图像，如图1b所示。

第2步，基于剪裁后的土壤CT图像进行孔隙结构辨识。而由于CT扫描仪受电路板等硬件的限制和扫描层厚等参数的约束，会导致土壤CT图像受到噪声的污染。因此，选用自适应中值滤波算法去除图像噪声的干扰，增强孔隙结构信息[14-15]。基于图1c所示的滤波图像，本文采用自适应模糊C均值算法完成孔隙结构的二值化[16]，结果如图1d所示，黑色结构为土壤孔隙。

图1 土壤CT图像Fig.1 Soil CT images

基于孔隙二值化图像进行三维重构，是构建孔隙骨架模型的最后一个预处理环节。为了保证三维模型的真实性和消除土壤样本由于移动、碰撞造成的畸变影响，本文选取土壤样本中间部位的216幅图像，采用光线投影法完成孔隙三维模型的重构[17]。如图1e所示，重构后模型的尺寸为289像素×289像素×216幅，可为后续土壤孔隙骨架模型的构建提供精准的数据基础。

2 研究方法

2.1 距离变换法

距离变换法是一种基于局部区域进行的赋值变换，其主要思想是计算并标记空间目标体素点到模型边界体素点的距离，并依据此距离完成骨架模型的构建[18]。对于三维离散图像，体素点(k,j,i)的距离变换值Dv的表达式为

(1)

(2)

式中d——体素点(k,j,i)到体素点(x,y,z)的欧氏距离

B——所有边界体素点的集合

v1、v2——体素点

距离变换法主要包括3个步骤：①采用式(1)和式(2)计算孔隙模型中所有体素点的距离变换值，组成距离变换矩阵。②选取距离变换矩阵中数值最大的体素点作为骨架模型的种子点，由式(1)、(2)可知，三维目标的中心体素点具有最大的距离变换值。③以种子点为起点，确定其26 邻域内距离变换具有局部极大值的体素点，该体素点即为下一个骨架点。重复步骤③，直至符合条件的体素点不再发生变化，连接所有体素点，则为孔隙骨架模型。

2.2 细化法

细化法的基本思想是通过逐步均匀地剥蚀模型中边界体素点，以获得连通性不变的骨架模型[19]。该方法运算过程由2部分组成：①细化条件的建立，这是构建骨架模型的核心问题和必备条件。②伪分支和毛刺的处理，这是保证孔隙骨架模型连通性、中心性和细化性的重要因素。

2.2.1细化条件的建立

本文基于ROCKETT[20]提出的单像素宽度细化算法，建立孔隙结构26邻域内的邻接矩阵，通过判断邻域内的中心体素点是否会影响骨架结构的连通性，来决定是否从现有骨架模型中删除该体素点，并通过不断迭代判断实现对骨架的剥蚀。在这一过程中，细化条件的建立需要保证骨架模型的连通性、细化性和中心性，考虑到土壤孔隙的特性，本文细化法共包含两个条件：

(1)为了保证骨架模型的连通性，所有删除的目标点都应保证在其26邻域内至少有2个相同的体素点。按照该条件进行模型遍历，直到生成的骨架模型中目标体素点的数目不再改变。

(2)由于孔隙结构细小不均匀的特性，图像噪声会引起骨架模型具有冗余的枝节，因此，在细化法中增加了一个基于阈值的限制条件。骨架阈值长度T设置为5个体素点。遍历所有骨架结构，将长度小于该阈值的骨架删除，以保证模型的细化性。

2.2.2伪分支和毛刺的处理

骨架化过程中，细化法仅考虑了模型的局部连通性，易导致初始骨架模型存在冗余的分支、毛刺以及缺口的现象。因此，为了保证孔隙骨架模型的连通性和细化性，需要对骨架模型进行去毛刺处理。

去伪分支和毛刺处理主要包括毛刺的删除和狭窄缺口的填补，其实现过程主要包括3个步骤：①依据某一准则判断出组成孔隙骨架中轴线的体素点。②以这些体素点组成的中心路径为标准，删除路径之外的冗余体素点，以去除骨架上的毛刺。③通过形态学操作，填补骨架路径的狭窄缺口，从而保证孔隙骨架模型的拓扑不变性。

在这一修正过程中，中心路径的确定对于骨架模型去毛刺处理的精度具有重大影响。本文通过3个步骤建立中心路径：①在连通域的两端分别指定一个起始点和一个终止点。②由起始点进行路径漫游，判断在26连通域内能达到终点的所有路径。③所有路径中的最短路径即为中心路径。以此为标准，可以快速精确地完成骨架模型的去毛刺处理。

3 实例应用与验证

为测试距离变换法和细化法在土壤孔隙骨架模型构建的可行性和精确性，选用2组自定义的规则结构、1组基于3D打印技术和CT扫描技术获得的规则圆柱体模型和12组基于二维土壤CT图像生成的孔隙模型为研究对象。通过对规则结构骨架模型和土壤孔隙骨架模型构建结果的比较，从细化性、中心性和连通性3个层面分析2种算法的骨架化性能。

为消除运行环境和计算机硬件对2种算法性能的影响，保证2种算法的可比性，所有试验均在同一台计算机上采用Matlab R2018a实现，计算机处理器为4.00 GHz Intel Core i7 4790，内存16 GB，操作系统为Windows 7。

3.1 规则结构的骨架模型

为详细比较2种算法对规则结构骨架模型的构建效果，选取了规则曲线、规则圆环和规则圆柱体进行骨架模型的构建。如图2所示，灰色区域为原始结构，红色曲线为提取的骨架模型。

由图2a、2b可知，距离变换法针对规则曲线和规则圆环构建的骨架模型具有明显的断裂，连通性较差；而且通过与原始结构的对比发现，其构建的骨架模型长度偏短，主要体现在骨架模型的两端(蓝色方框所示)。相较于距离变换法，细化法提取出的骨架结构没有出现明显的断裂，而且在首端和尾端也没有出现骨架缺失的情况，具有较好的连通性。

由图2c、2f蓝色方框可知，对于规则圆柱体模型，两种算法构建的骨架结构两端均没有出现明显的缺失现象。但是，在圆柱体直径较小时，距离变换法构建的孔隙骨架存在多处断裂的情况，而细化法构建的骨架模型则在很大程度上改善了这一问题。综上所述，细化法构建的骨架模型与真实情况更为一致。

3.2 土壤孔隙骨架模型

图3为2种算法针对土壤孔隙骨架模型的构建结果。为详细比较2种算法对土壤孔隙骨架模型的构建细节，随机选取了原状土壤样本中的两个大孔隙结构进行比较分析。图3a、3b、3d、3e所示为两个大孔隙A、B骨架模型的放大图。

由图3a、3b、3d、3e可以看出，距离变换法和细化法都能得到较为清晰的土壤孔隙骨架模型，并分列于相应原孔隙的中心。但是距离变换法出现断裂的情况，破坏了骨架的连通性，基于该孔隙骨架模型不利于对孔隙特征的量化分析。这一原因主要是因为距离变换法在局部区域可能没有绝对极大值，从而难以准确判定骨架体素点的位置，导致体素点偏离中心。相比较而言，细化法能够定义骨架模型的简单点并进行循环判断，保证骨架模型具有较好的连通性；并通过去伪分支和毛刺的处理避免了体素点重复和骨架存在狭窄缺口的情况，保证了骨架的体素点处于孔隙的中心位置。

如图3c、3f所示，在真实土壤孔隙骨架模型中，单个体素点之间存在空隙，这是由于图像尺度增大导致的视觉效果。由图3c、3f的放大图可知，距离变换法仍存在大量骨架结构缺失，对于部分体素点也出现了偏移中心位置的现象；而且局部区域也出现了多个体素点重叠的情况。通过对整个骨架模型的分析，发现距离变换法的细化性和连通性较差。反之，细化法的骨架结构完整，具有单体素点的特征，也处于土壤孔隙的中心位置，具有良好的连通性、细化性和中心性。

3.3 骨架模型中心性评价

为了更精确评价2种骨架化算法的性能，本文采用中心性作为定量评价标准。由于该指标均需要基于标准骨架结构进行分析，而土壤孔隙的真实骨架模型难以确定，因此，试验选用CT扫描的规则圆柱体模型进行量化试验的测试对象。

中心性表示实际的骨架结构S(i)与构建的骨架模型S′(i)之间的偏差程度。根据欧几里德理论，中心性Cd的计算公式为

(3)

式中K——骨架的数量

i——骨架结构的序号

由式(3)可知，中心性表示构建的骨架模型偏离原始结构中心位置的距离，其值越小，构建的骨架模型与真实的骨架模型越接近，则说明算法的中心性越好。图4为2种骨架模型构建算法的中心性评价结果。

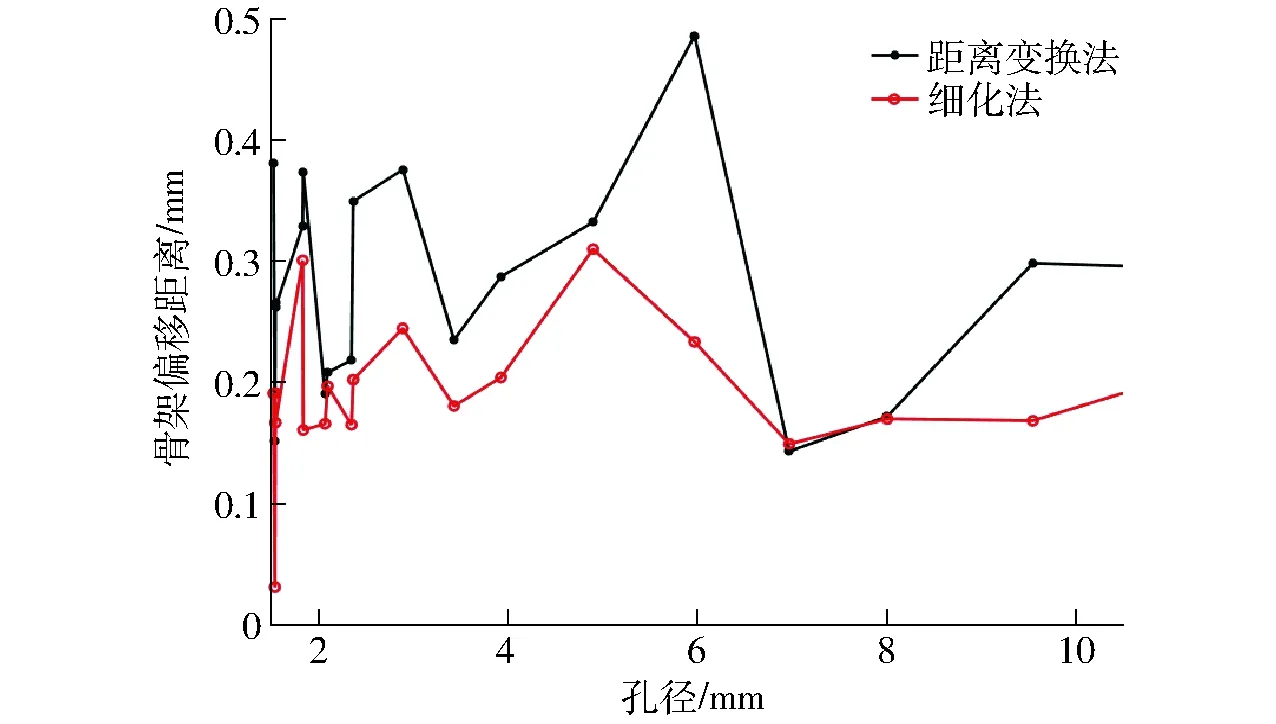
图4 圆柱体模型中心性评价结果Fig.4 Evaluation results of centrality

由图4可以看出，两种算法的骨架偏移距离和圆柱体的孔径没有明显的关系。不论圆柱体的孔径多大，细化法的骨架偏移距离一直小于距离变换法。细化法平均骨架偏移距离为0.10 mm，距离变换法则为0.15 mm。骨架偏移距离越接近0，表示中心性越好，因此，细化法的平均中心性优于距离变换法。此外，细化法的方差为0.05 mm，仅为距离变换法(0.12 mm)的2/5倍，由此可知，细化法针对不同直径的孔隙结构具有更为稳定的性能和更强的鲁棒性。

结合规则几何结构和土壤孔隙结构的试验结果可知，细化法构建的骨架模型具有良好的细化性、连通性和中心性，能够更好地保留土壤孔隙结构的拓扑特性，可为土壤孔隙结构的空间分布研究提供一种先进的技术手段。

4 结论

(1)针对自定义规则结构和土壤孔隙结构的骨架模型构建试验可得，距离变换法和细化法的骨架模型构建效果均不受模型类型的影响。其中，距离变换法构建的骨架模型中存在部分体素点缺失和偏移的现象，使得骨架的实际长度小于真实情况。而细化法构建的骨架结构则避免了这一问题，骨架模型具有良好的连通性和细化性。

(2)通过对2种算法中心性的量化分析可得，细化法的平均骨架偏移距离为0.10 mm，比距离变换法(0.15 mm)减少了50%，说明细化法具有更强的鲁棒性，更加适用于不同孔径的土壤孔隙结构。

(3)通过对骨架模型连通性、细化性和中心性3个指标的定性和定量分析发现，细化法具有优越的描述土壤孔隙形状及拓扑特征的能力，可进一步应用于土壤物理结构及水文特性的探索研究。