一种预测型电流模式数字控制的单电感双输出降压型DC-DC转换器

袁文瑞，闫 娜，谈 熙，闵 昊

(复旦大学 专用集成电路与系统国家重点实验室，上海 201203)

基于电感的DC-DC转换器是利用电感以电磁场储存能量来实现电压转换，具有较高的转换效率和较大的驱动能力，所以在电源管理模块(Power Management Unit, PMU)中得到了广泛的应用.但是由于电感本身体积较大，所以电感型DC-DC转换器整体的体积较大，成本较高.而且，随着智能手机、可穿戴设备等便携式电子设备小型化、智能化、复杂化的发展趋势，电源管理模块需要为不同的模块提供多个不同的工作电压.按照传统的解决思路，需要多个电感型DC-DC转换器才能产生多个不同的输出电压，而所需电感数量的增加会进一步导致体积和成本大大增加.为了在保持高效率、多输出的同时降低成本，单电感多输出(Single-Inductor Multiple-Output, SIMO)的DC-DC转换器结构被提出，该结构可以利用一个电感来产生多路不同的输出电压，从而可以有效地减小所需电感数目.但是，由于单电感多输出DC-DC转换器结构和控制方法的复杂性，所以在诸如转换效率、输出电压纹波、控制算法复杂度、交调影响方面存在着问题和难点.

针对上述存在的问题，研究人员提出了不同的系统架构和控制算法.文献[1]采用了一种分时控制的方法，即在一个开关周期内只对一路输出进行充电，而多路输出则通过在多个开关周期内轮流对每一路输出充电实现.该种控制方法中每次开关周期结束后电感电流都会归零，所以工作于离散导通模式(Discontinuous Conduction Mode, DCM)，各路输出之间完全独立，因而没有交调影响的问题.然而由于转换器必须始终工作于DCM模式，导致其驱动能力有限，而且由于整个完整的开关周期较长，使得每个输出的电压纹波较大，且瞬态响应速度较慢.为了解决驱动能力较低的问题，文献[2]提出了一种伪连续导通模式，这种控制方法是将每一个开关周期结束后的电感电流值由归零改成一个固定的电流值，然后通过一个续流开关将能量保存到电感中，从而可以提高负载驱动能力.各路输出之间仍然是相互独立的，所以同样没有交调影响.但是由于增加了续流开关，会引入额外的开关损耗和导通损耗，降低整体的转换效率，同时也会增加模块体积.文献[3-4]采用了脉冲宽度调制模式(Pulse Width Modulation, PWM)的单充多放控制方法，即在一个开关周期内轮流对多路输出进行充电，其中文献[3]采用模拟控制方式实现，文献[4]采用数字控制方式实现.在这种控制方法中，所有输出变量通过线性组合得到反馈变量，然后对每一个反馈变量按照PWM调制进行环路补偿，进而得到总体的能量产生占空比和每一路输出对应的能量分配占空比.这种控制方法中DC-DC转换器工作于连续导通模式(Continuous Conduction Mode, CCM)，驱动能力较强，输出电压纹波较小，但是各个输出之间相互影响，交调影响问题较为严重，且环路补偿设计较为复杂.文献[5-7]采用了基于比较器控制的单充多放控制方法.文献[5]中的控制原理是前N-1路通过比较器比较反馈电压和基准电压来轮流选通每一路进行能量分配，而总体能量产生则根据第N路输出采用传统的PWM调制方法控制；文献[6-7]则是采用比较器和锁相环(Phase Locked Loop, PLL)相结合的控制方法，根据每一路输出的误差信号之和利用PLL控制总体的能量产生.虽然前N-1路输出采用比较器控制使得相互之间没有交调影响，但是无论采用PWM调制还是PLL控制整体能量的产生，都会使得最后一路输出受到前面几路输出的影响，交调严重.

通过对单电感多输出DC-DC转换器现有研究成果的调研，可以看到每一种结构和控制方法都有各自的优缺点，在驱动能力、电压纹波、控制复杂度、转换效率和交调影响之间有着各自的权衡.针对这些问题，本文提出了一种基于电流模式的数字控制的预测算法，在保证转换效率和电压纹波的同时可以尽可能地减小各路输出之间的交调影响.本文以单电感双输出(Single-Inductor Dual-Output, SIDO)降压型DC-DC转换器为例分析具体的控制方式和预测算法，并进行系统仿真验证.

1 单电感双输出降压型DC-DC转换器的系统结构

基于电流模式数字控制的单输出DC-DC转换器的预测算法[8-10]，本文提出了一种针对单电感多输出的滞后边沿调制的谷值电流控制的预测算法，并应用到SIDO降压型DC-DC转换器中.其系统结构如图1所示.在此系统架构中，主要有4个模块: 电压控制模块(Voltage Controller)、电流估算模块(Current Estimation)、电流控制模块(Current Controller)和数字脉冲宽度调制模块(Digital Pulse Width Modulation, DPWM).电压控制模块对反馈的误差电压进行比例-积分(Proportional-Integral, PI)补偿，得到各个电流基准值；电流估算模块基于输入输出电压对电感电流谷值进行估算，从而不需要电流检测模块；电流控制模块根据表征每路输出负载电流的电流基准值以及电感电流估算值和表征总电流的电流基准值之间的误差计算下一个开关周期所需要的各个占空比；DPWM模块根据计算的占空比产生对应的开关控制信号.

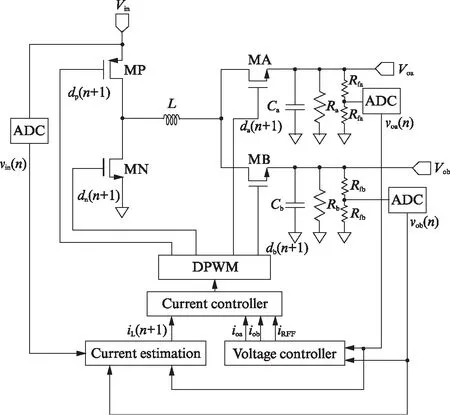
图1 预测型电流模式数字控制单电感双输出降压型DC-DC转换器的系统架构Fig.1 Architecture of predictive current-mode digital controlled SIDO DC-DC converter

1.1 电感电流谷值估算

本文设计的DC-DC转换器采用电流模式控制，所以除了输出电压之外，还需要获取电感电流信息.传统的解决方案是采用一个高速高精度的电流检测电路对DC-DC转换器的电感电流进行检测，然而低损耗、高速、高精度的电流检测电路是以复杂、高成本为代价的.所以在本文中，我们不采用电流检测模块，而是基于电感电流波形，根据当前电感电流值对下一个开关周期的电感电流进行估算.因为本文的DC-DC转换器采用滞后边沿调制的谷值电流控制，所以这一节我们研究对电感电流谷值进行估算的方法.

相邻两个开关周期内的电感电流波形如图2所示.由于输入电压和输出电压变化缓慢，所以可以认为在相邻两个开关周期内保持不变.在nTs～(n+dI(n))Ts时间内，PMOS功率开关MP导通，NMOS功率开关MN关断，输入对电感充电，在(n+dI(n))Ts～(n+1)Ts时间内，PMOS功率开关MP关断，NMOS功率开关MN导通，电感对输出放电；在nTs～(n+da(n))Ts时间内，NMOS输出开关MA导通，NMOS输出开关MB关断，输出A与电感相连，在(n+da(n))Ts～(n+1)Ts时间内，NMOS输出开关MA关断，NMOS输出开关MB导通，输出B与电感相连.nTs时刻的电感电流谷值为iL(n)，(n+1)Ts时刻的电感电流谷值为iL(n+1)，在输入输出电压、电感值和第n个开关周期内的占空比信号dI(n)、da(n)、db(n)已知的情况下，可以根据iL(n)计算出iL(n+1)的值.

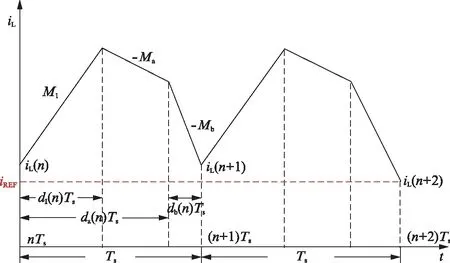
图2 单电感双输出降压型DC-DC转换器的电感电流波形Fig.2 Inductor current waveform of proposed SIDO DC-DC converter

M1，Ma，Mb分别表示3个时间段内的电感电流斜率，可以表示为

(1)

则第n+1个开关周期起始时刻(n+1)Ts的电感电流谷值iL(n+1)可以表示为:

(2)

其中:Vin表示采样的输入电压值；Va表示输出A的输出电压采样值；Vb表示输出B的输出电压采样值；L表示电感值；Ts表示开关周期.

实际上，由于4个开关管的寄生电阻和电感的寄生电阻的存在，利用式(2)进行的电感电流谷值估算与实际的电感电流谷值之间存在着一定的偏差，这个偏差会导致稳态情况下输出电压的误差.所以，为了使得电流估算值与实际值相吻合，消除输出电压的稳态误差，我们将开关管和电感的寄生电阻考虑进去.考虑到这些寄生参数后的电感电流斜率可以表示为

(3)

其中:Rp，Rn表示功率级开关管的寄生电阻；Rout表示输出开关管的寄生电阻；RL表示电感的寄生电阻；IL表示电感电流谷值.在这里为了分析和计算简便，将电感电流纹波忽略不计，所以直接采用电感电流谷值来近似代替电感电流平均值.

考虑了上述寄生参数之后，在第n+1个开关周期起始时刻的电感电流谷值iL(n+1)可以改写为

(4)

根据此修正后的估算公式，电感电流谷值的估算可以实现较高的精度，与实际电感电流谷值的偏差也可以基本消除.

采用式(2)或式(4)的公式，利用迭代的方法，则可以在不直接检测电感电流的情况下获取电感电流信息.

1.2 占空比预测算法

本文设计的单电感双输出DC-DC转换器中电感的充放电时间和每路输出的选通时间由占空比预测算法决定.占空比预测算法就是在当前开关周期内基于表征每路输出负载电流的电流基准值预测下一个开关周期的各路能量分配占空比，以及根据电感电流谷值与表征总能量的电流基准值之间的误差预测下一个开关周期的能量产生占空比.利用预测算法来计算每个开关周期内的所有开关的最优的开关时间，从而使每个输出电压的变化只受自己负载电流变化的影响.

在第n+1个开关周期内，补偿后的电流信号ioa和iob分别表征了输出A和输出B的负载电流，电流基准值iREF表征了所有输出总的负载电流(iREF=ioa+iob).在忽略电感电流纹波的情况下，可以列出:

(5)

根据式(5)可以求出预测的第n+1个开关周期内的能量产生占空比dI(n+1)和能量分配占空比da(n+1)、db(n+1)分别是:

(6)

式(6)就是SIDO降压型DC-DC转换器的基本的占空比预测算法.由式(6)可知，各路输出对应的能量分配占空比(da、db、…)都是基于表征本输出负载电流的电流基准值(ioa、iob、…)进行计算，只与本输出有关，而独立于其它路输出.而总能量产生占空比则消除电感电流与各路输出总体负载电流之间的误差.因而采用这种占空比预测算法可以有效减小交调影响.

1.3 负载跳变与交调影响分析

对于SIMO转换器而言，不同输出之间的交调影响是其最重要的问题.SIMO转换器每一路输出的负载跳变都有可能会影响其他路输出，从而导致其他路输出出现过冲或欠冲的交调影响，所以需要对SIMO转换器的负载跳变进行分析，根据式(6)分析本文提出的预测算法在发生负载跳变时如何快速响应并减小交调影响.图3显示了单电感双输出DC-DC转换器中输出A的负载电流IOA发生跳变后，电感电流IL和能量产生占空比(DUTY)的波形示意图.

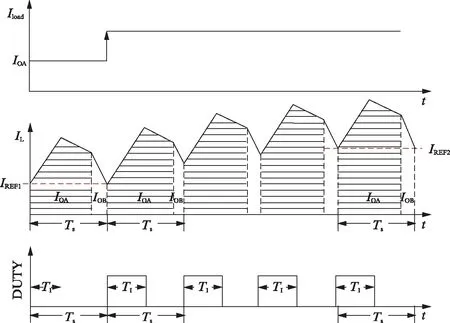
图3 单电感双输出DC-DC转换器负载跳变示意图Fig.3 Load transient waveforms of SIDO DC-DC converter

当输出A的负载电流IOA增大时，输出电压VOA变小，经过电压控制模块产生的电流基准值ioa会增大，iob保持不变，而iREF=ioa+iob同样会增大.由式(6)可知，在负载电流跳变后的一个周期里，能量产生占空比dI和输出A对应的能量分配占空比da增大，对输出A的充电时间增加来满足增大的负载电流.由于能量产生占空比dI增大，导通时间变长，电感电流IL增大，所以虽然输出B对应的能量分配占空比db减小，增大的电感电流使得对输出B的充电电荷总量保持不变，即对输出B不会产生影响(由式(6)的变形db(n+1)iL(n+1)=iob可知输出B的能量分配占空比和电感电流的同步变化能够满足其负载电流的需求，从而保持其不受输出A负载电流变化的影响).经过几个开关周期的调整之后，电感电流谷值IL稳定在新的电流基准值IREF2处，重新稳定后，能量产生占空比dI和输出A对应的能量分配占空比da变大，而输出B对应的能量分配占空比db则会变小.

经过分析可知，在负载跳变过程中，由于采用占空比预测算法，在当前开关周期对下一个开关周期的占空比进行预测，所以理论上能量调整可以在几个周期内快速完成，响应速度比较快.对于其他输出，虽然在调整过程中充电时间减小，但是由于电感电流同步增加，所以使得在每一个开关周期内每路输出对应的充电面积基本不变，即对每路输出的充电电荷基本不变，满足各路输出负载电流的需求，所以输出电压基本不会发生波动.

由此可见，式(6)的占空比预测算法，基于每一路输出负载电流独立调整对应的能量分配占空比，基于电感电流与电流基准值的误差同步调整电感电流，从而可以保证一路输出的负载跳变不会对其他路输出产生影响，减小交调影响.

2 单电感双输出降压型DC-DC转换器的小信号模型

如图1所示，在单电感双输出DC-DC转换器中，电压控制模块对误差电压进行环路补偿，得到基准电流:ioa、iob、iREF传递到电流控制模块用于占空比的预测.为了对电压控制模块中的环路补偿器进行设计，首先需要分析单电感双输出DC-DC转换器的环路小信号模型.本设计中的DC-DC转换器采用电流控制模式，将电感电流和输出电压同时作为反馈变量，构成电流反馈环路和电压反馈环路两个控制环路.采用电流控制模式可以提高环路的瞬态响应速度，也使得从控制器到功率级输出端的传输函数只有一个实极点，有利于稳定性补偿.

本文设计的SIDO降压型DC-DC转换器的小信号模型如图4所示.该小信号模型对2个环路之间实际上可能存在的电路耦合和相关性进行了一定简化，从理论分析上来看，该简化具有合理性与可行性.单电感双输出DC-DC转换器由2个环路构成，下面是输出A的反馈环路，上面是输出B的反馈环路.在小信号模型中，输出A的反馈环路没有受到输出B的影响，而在输出B的反馈环路中，2个输出通过电压反馈环路得到的基准电流(ioa(s)、iob(s))相加进入到电流反馈环路得到稳定的电感电流iL(s)，而后又减掉了输出A的电流量ia(s)而得到输出B的电流量ib(s)，经过这样的相互抵消之后，理论上输出B的环路增益不会受到输出A的影响.所以经过合理的模型简化后，理论上2个环路之间基本相互独立.以环路A为例分析其开环传输函数.

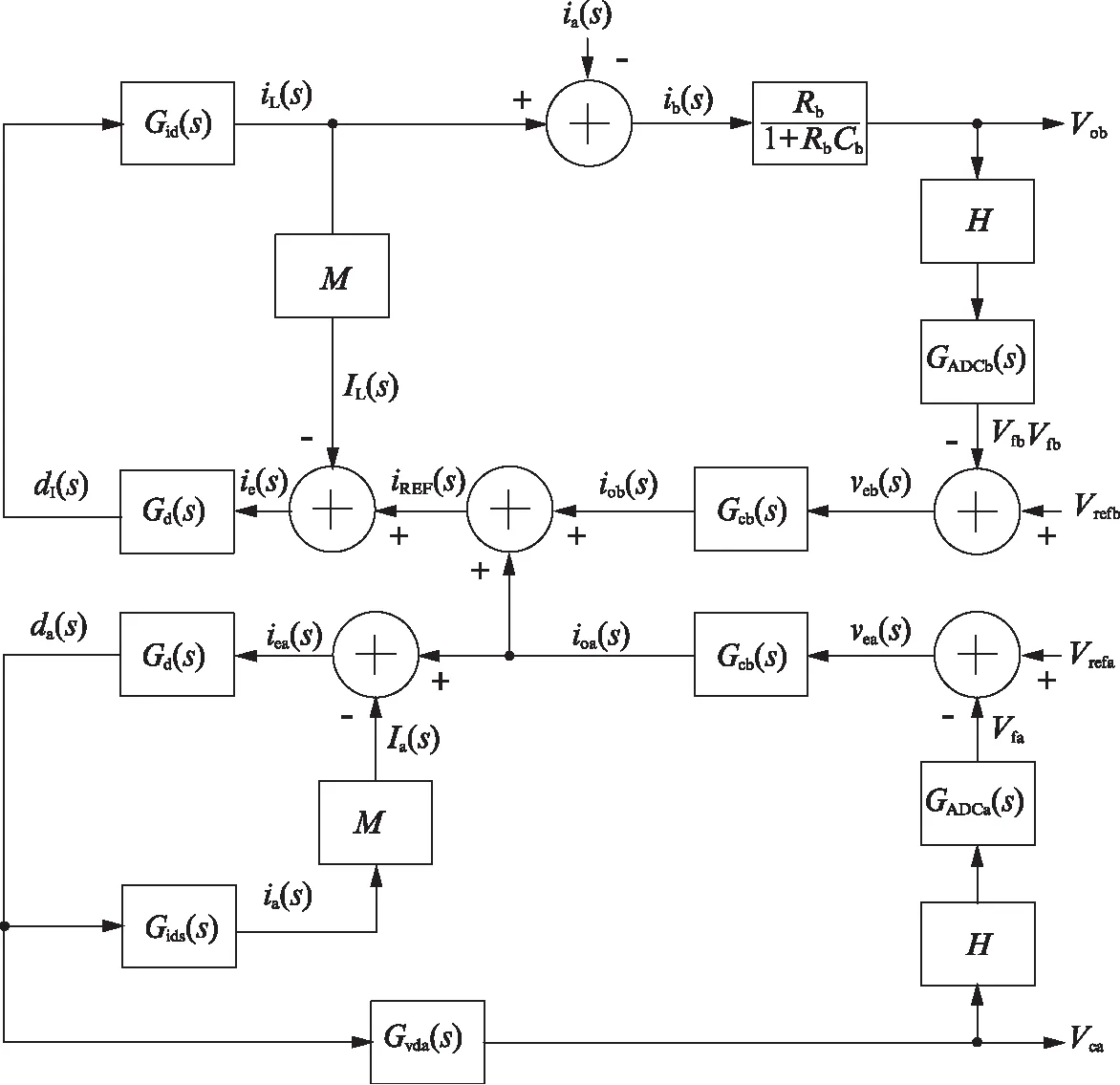
图4 单电感双输出降压型DC-DC转换器的小信号模型Fig.4 The complete small signal model of SIDO DC-DC converter

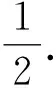
GADCa(s)表示模数转换器(Analog-to-Digital, ADC)模块的传输函数，可以表示为

(7)

其中τadc表示ADC模块的采样延时.这里不单独考虑这个延时，而是在整个环路传输函数中将ADC的采样延时、数字控制模块的计算延时和DPWM模块的延时作为一个整体考虑，记为τdelay；Vq表示ADC模块的量化精度.

Gca(s)表示PI补偿器的传输函数.由于采用电流控制模式，DC-DC转换器的功率级传输函数中只存在一个实极点，所以可以采用PI补偿器进行补偿.PI补偿器的传输函数可以表示为

(8)

由于电流反馈环路的瞬态响应速度远远大于电压反馈环路，所以电流环路的闭环传输函数可以用单位1来代替.则从电流基准值ioa(s)到数字控制器中的电感电流值Ia(s)的传输函数可以表示为

(9)

其中M表示从实际的电感电流值到数字域中的电感电流值的比例系数.

所以从电流基准值ioa(s)到占空比da(s)的传输函数可以表示为

(10)

其中Gida(s)表示从占空比到电感电流的传输函数.另有Gvda(s)表示从占空比到输出电压的传输函数，二者可以表示为

(11)

(12)

根据上述各个模块的传输函数，可以求出输出A环路的开环传输函数，表示为:

(13)

对环路B来说，在电流反馈环路之前加入的输出A的基准电流在电流环路之后又相应减去，从而相互抵消，其反馈环路的开环传输函数可以表示为:

(14)

根据式(13)和式(14)，对于输出A的环路增益是与输出B无关的，而对于输出B的环路增益经过相互抵消之后也是不受输出A的影响的.所以由图4经过一定简化的小信号模型得到的2个环路的开环传输函数形式基本相同，且2个环路之间相关度很低，基本互不影响.

3 单电感双输出降压型DC-DC转换器的仿真结果

为了对本文提出的基于电流模式的数字控制方式和占空比预测算法进行验证，我们设计了一个单电感双输出降压型DC-DC转换器，通过仿真来分析验证.SIDO降压型DC-DC转换器的设计参数如下:VIN=2.5V，VOA=1.2V，VOB=1.6V，L=4.7μH，COA=COB=10μF，f=1MHz.以下仿真结果为系统的前仿真结果.

图5和图6分别是单电感双输出DC-DC转换器在负载电流为100mA和200mA下的稳态输出电压波形.在2路输出的负载电流都为100mA时，单电感双输出DC-DC转换器能够达到稳定状态，稳态下两路的输出电压为:VOA≈1.21V，VOB≈1.61V，电压纹波分别为:Vripple_a≈7.13mV，Vripple_b≈5.86mV.在负载电流都为200mA时，稳态下2路的输出电压为:VOA≈1.22V，VOB≈1.60V，电压纹波分别为:Vripple_a≈13.58mV，Vripple_b≈13.26mV.

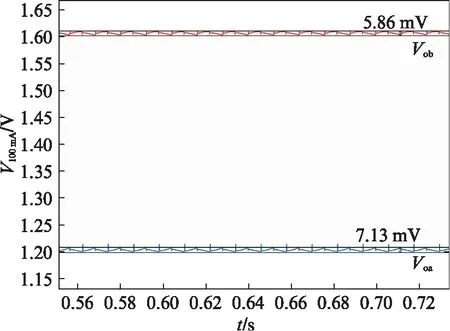
图5 负载电流为100mA时的稳态输出电压波形Fig.5 Output voltage waveforms at the load current of 100mA in steady state

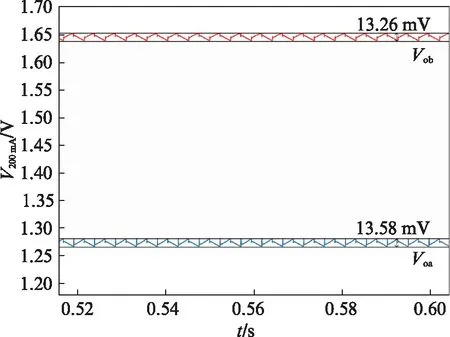
图6 负载电流为200mA时的稳态输出电压波形Fig.6 Output voltage waveforms at the load current of 200mA in steady state

图7是输出A发生100mA的电流跳变时的瞬态响应波形(初始电流状态:IOA=100mA，IOB=100mA).从图中可以看到，当输出A发生100mA的电流跳变时，输出A的输出电压的欠冲电压和过冲电压分别是38.86mV和40.72mV，而输出B对应的过冲电压和欠冲电压分别是20.05mV和19.84mV.图8是输出B发生100mA的电流跳变时的瞬态响应波形(初始电流状态:IOA=100mA，IOB=100mA).当输出B发生100mA的电流跳变时，输出B的输出电压的欠冲电压和过冲电压分别是40.25mV和35.09mV，而输出A对应的过冲电压和欠冲电压分别是21.64mV和16.83mV.

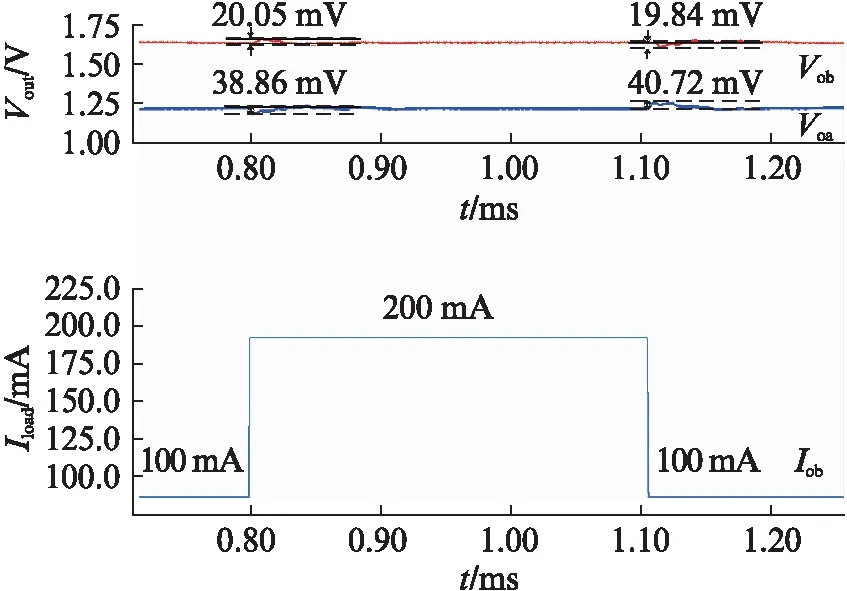
图7 输出A发生100mA的电流跳变时单电感 双输出DC-DC转换器的瞬态响应波形Fig.7 Transient waveforms of SIDO buck converter with 100mA load current step condition at output A

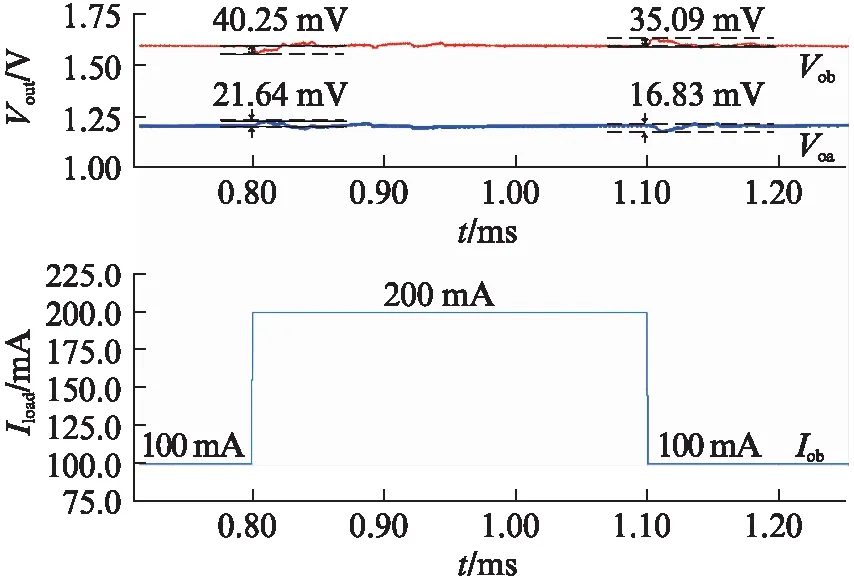
图8 输出B发生100mA的电流跳变时单电感 双输出DC-DC转换器的瞬态响应波形Fig.8 Transient waveforms of SIDO buck converter with 100mA load current step condition at output B

从瞬态响应仿真结果可以看出，未发生负载跳变的支路电压过冲较小，小于发生负载跳变支路的电压过冲量.由此可见，本文提出的占空比预测算法可以有效减小各路输出之间的交调影响.

4 结 语

本文设计了一种预测型电流模式数字控制的单电感双输出降压型DC-DC转换器.所采用的占空比预测算法可以在当前开关周期内根据输入输出电压值、系统参数和电流基准值计算出下一个开关周期所需要的能量产生占空比和能量分配占空比，从而实现系统稳定和快速响应.由于每一路输出对应的能量分配占空比的计算都是基于表征自身负载电流的电流基准值，所以不同输出之间的控制环路和占空比在理论上是相互独立的，从而减小了不同输出之间的交调影响.本文对基于预测型电流模式数字控制方法设计的降压型双输出DC-DC转换器进行了系统仿真，验证了这种控制方式和预测算法的可行性与正确性.