郑州市房地产投资与经济增长的关系分析
胡清华,邵明振
(河南大学 经济学院,河南 开封 475000)
一、引言
推动经济增长的三驾马车分别是消费、投资与出口。其中,投资的增长对经济的增长有着很大的拉动作用。对固定资产的投资来说,房地产投资是最重要的部分,可以说是我国国民经济增长的龙头。[1]近年来,河南省经济一直呈现快速增长的趋势,在习近平新时代中国特色社会主义思想的引导下,主动融入一带一路,不断迸发出活力与光彩。作为河南省省会的郑州,凭借着中原经济区的地理优势和郑汴一体化、郑东新区的发展,经济在快速地增长。其关键的因素就在于房地产投资。
(二)研究意义
近年来,河南省总体经济实力迈上了更高的台阶,特别是近五年来,河南省的变化可谓日新月异。中原崛起计划中,河南省经济的发展做出了很大的贡献。与此同时,作为河南省的省会郑州,凭借着中原经济区的地理优势和国际综合交通枢纽的战略地位,经济也在飞速地增长。在经济发展的过程中,郑州市的房地产投资有没有促进郑州经济的增长,或者说,郑州经济的增长反过来有没有促进房地产投资呢?对于这一问题,本文以郑州市房地产投资额和生产总值1995-2017年的时间序列数据为例对二者的关系进行实证分析以达到研究的目的,并根据结论为郑州市的房地产业的发展提供建议,为郑州市的房地产投资与经济增长之间协调发展提供建议。
二、实证分析
(一)变量的选择和数据来源
本文选取郑州市房地产投资额(REI)作为房地产投资规模的衡量指标,郑州市生产总值(GDP)作为郑州市经济增长的衡量指标,选取1995—2017年郑州市房地产投资额和生产总值的时间序列数据。所有数据均来源于《郑州市统计局》。为了更进一步地看出郑州市房地产投资与经济增长之间的相关关系,通过借助Eviews软件得到两者的散点图和计算出两者的相关系数。二者的散点图如图 1所示,从中可以看出,郑州市房地产投资额和地区生产总值的变化趋势高度相似。表1中得出二者的相关系数为0.963068,表明郑州市房地产投资额与地区生产总值有高度相关性。
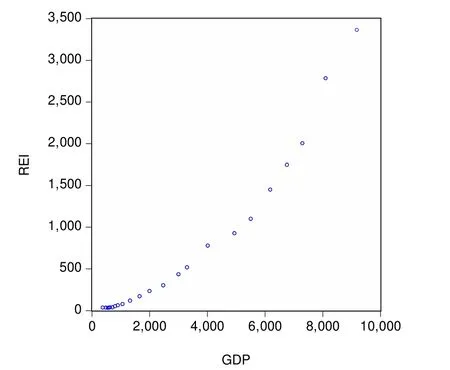
图1 郑州市房地产投资与地区生产总值散点图
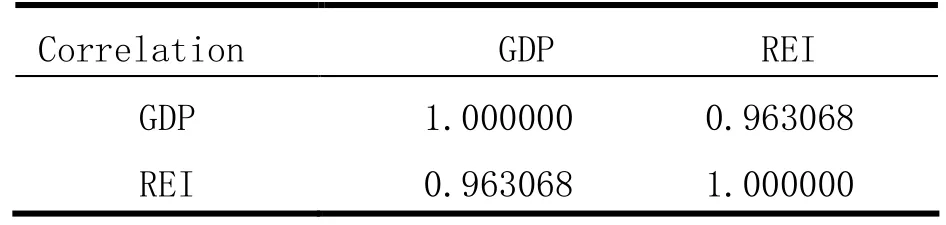
表1 GDP与REI的相关系数检验
(二) 平稳性检验
本次研究所涉及的数据都是时间序列数据,需要对数据进行平稳性检验。这可避免对非平稳的时间序列数据进行回归时出现伪回归的现象。在平稳性检验的方法中,大多使用的是迪基—福勒检验(DF检验)、菲利普斯—配荣检验(PP检验)以及恩格尔和柳(Engle&Yoo,1987)提出的 ADF(Augmented Dickey-fuller Test)检验。[2]其中,对于ADF检验来说,这个方法适用于出现具有高阶自相关问题的时间数列数据。本文通过数据处理发现,郑州市的房地产投资额REI和生产总值这两个时间序列数据是高阶自相关的,所以在这里我们主要运用的是ADF检验法。首先对REI和GDP作自然对数变换,这样做不改变数据原有的关系,而且有助于消除异方差和趋势线性化现象,变换后两者分别用 LnREI和 LnGDP表示,一阶差分用Δ LnGDP、ΔLnREI 表示。在检验中,原假设设为序列存在单位根。[3]Eviews软件对这些序列进行单位根检验,可以得出结果和分析。从表 2中我们可以看出,LnGDP原序列的ADF值为0.0916,大于5%显著性水平下的值为-3.0124。说明 LnGDP序列是不平稳的,不能拒绝在上文中做出的原假设,同样单位根检验的结果中 LnREI的序列也是不平稳的。此时需要对各原序列进行差分处理,如表中所示。GDP序列一阶差分后的ADF值为-3.1367,REI序列一阶差分后的ADF值为-3.1922。这两个数都小于 5%显著性水平下的临界值-3.0124,说明郑州市房地产投资额与郑州市地区生产总值这两个序列均为一阶单整序列,他们之间可能存在某种平稳的线性关系,接下来用协整检验和误差修正模型来研究二者关系。

表2 综合检验结果
(三)协整检验
在分析过程中,一般使用的检验方法有E-G两步法协整检验以及 Johansen协整检验。其中 E-G两步法协整检验是适用于只包含两个研究变量的检验。[4]本文研究的要素是郑州市房地产投资 REI和经济增长GDP两个变量,所以我们选择E-G两步法协整检验方法来进行分析。
在上面我们运用了ADF单位根检验,发现房地产投资额与地区生产总值序列满足同阶单整,满足了E-G两步法协整检验的使用条件。在接下来的检验中,我们以LnGDP为因变量,LnREI为自变量开始进行协整检验。
首先用 Eviews软件中普通最小二乘法估计LnGDP和LnREI之间的数量关系,得出二者的回归方程,同时也得出 et(非均衡误差)。接下来对非均衡误差项做单位根ADF检验,通过比较结果,来判断et是否平稳。
先用软件对LnGDP和LnREI序列进行最小二乘估计,如下所示,对于得到的结果(见表 3)我们做出相应的分析。

表3 LnGDP和LnREI序列的OLS估计
从表3可以得到回归方程


其中我们可以看出方程的可决系数 R²为0.987524,方程的拟合度较高,所对应的P值为0,说明效果很显著,说明该方程的估计系数均通过显著性检验。
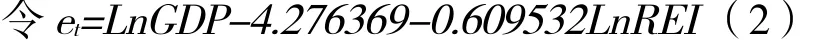

表4 et单位根检验结果
表4显示的是对残差序列做了单位根ADF检验之后得出来的结果。从表中的结果可以看出,检验的t值为-5.8197,而检验的5%显著性水平下的临界值是-1.9572,二者相比还是 t值较小,说明 et是平稳的序列,检验的结果是平稳的。由此可以得出 LnGDP和 LnREI之间存在着长期的协整关系。(3)被称为协整方程,说明LnGDP和LnREI的线性组合也是平稳的。另外从协整方程式我们还可以得到,郑州市房地产投资每增加百分之一,郑州市的生产总值相应的平均增加0.609532%,这个数据分析表明郑州市房地产投资对郑州市的经济增长贡献是很大的。
(四)误差修正模型
从上述协整检验可以分析得出郑州市房地产投资和经济增长之间具有协整关系,二者长期的变化趋势是一致的。由于各种原因,在短期内二者的关系或者走势或多或少会出现不平衡的现象。因此,接下来建立修正误差模型,也是为了改善长期静态模型的一些缺点。
建立误差模型如下所示:
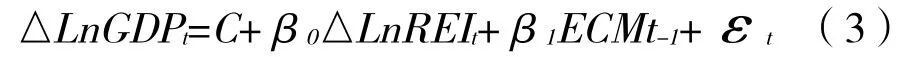
ECM表示误差修正项。回归结果如表5所示
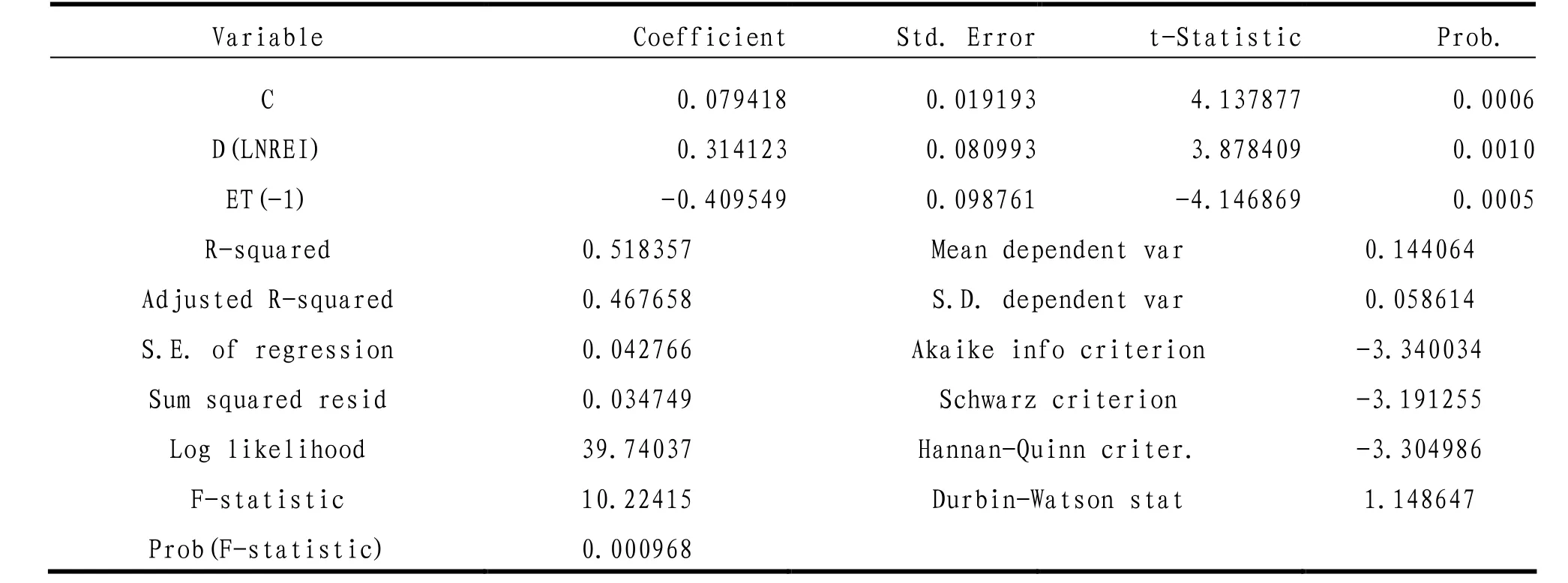
表5 修正误差模型估计

该模型的结果表明,短期内房地产投资每增加1%,郑州市的GDP增长0. 31412%,LnREI的短期波动对LnGDP有着显著的正影响。另外模型中得到ECMt-1的系数为-0.40955,-0.40955<0,是符合反向修正机制的。所以由修正误差项通过反向修正机制可以得出郑州市房地产投资与经济增之间存在着动态均衡机制。且ECMt-1的系数也表明了,如果郑州市经济偏离系统的均衡状态时,修正误差项会在下一期以0.40955的力度给调整回来。
(五)Granger因果关系检验
郑州市房地产投资额与地区生产总值序列是满足同阶单整的,上文中对LnGDP和LnREI序列进行协整检验,从协整检验的结果得到了二者之间存在长期的协整关系。那么关于二者之间是否存在因果关系,或者说郑州市房地产投资与经济增长之间谁是因谁是果,我们将采用Granger因果关系检验的方法对二者继续检验。[5]
根据检验的结果(表6),在滞后期为一年时,LnGDP不是 LnREI的格兰杰原因的概率为0.0048,这个值相对于置信水平0.05来说还是很小的,所以在这里我们拒绝原假设,即郑州市经济增长是房地产投资的格兰杰原因,而LnREI不是LnGDP的格兰杰原因的概率为0.1193,大于置信水平 0.05,这时候接受原假设,LnREI不是LnGDP的格兰杰原因,郑州市房地产投资不是带动郑州市经济增长的格兰杰原因,说明郑州市房地产投资与经济增长之间存在着单向的因果关系;按同样的置信水平和分析方法分析滞后期为2年时候的情况,发现与滞后期为 1年的情况是相同的;在这里我们仅把滞后期为3年得出的数据写在了表6里面(滞后期为3年以上时分析的结果是类似的),从结果可以得出,都接受了原假设,说明LnREI不是LnGDP的格兰杰原因。反过来也不成立,二者不存在因果关系。

表6 Granger因果关系检验结果
三、实证结论及政策建议
(一)结论
1.从协整检验的结果来看,郑州市房地产投资额与GDP之间存在有协整关系,即二者具有长期的均衡关系。从得出来的协整方程中可以得出,LnREI 前面的系数为0.609532,说明了郑州市经济的增长对房地产投资的弹性系数为0.609532。郑州市可以适当增加对房地产业的投资,因为郑州市房地产业的发展较大地影响着郑州市的经济发展。
2.从建立的修正误差模型中,得出的结论是LnREI的短期波动对LnGDP有着显著的正影响,说明短期内房地产投资每增加 1%,GDP增长0.31432%。且ECMt-1的系数也表明了,如果郑州市经济偏离系统的均衡状态时,修正误差项会在下一期以0.40955的力度给调整回来。
3.从格兰杰因果检验可知,滞后期为 1年或者2年的时候情况是一样的,在显著性水平为5%的情况下都拒绝原假设,也就是说LnGDP是LnREI的格兰杰原因,即郑州市的经济增长是房地产投资的格兰杰原因,而房地产业投资的发展不是郑州市经济增长的原因,表明了郑州市房地产投资与经济增长之间存在着单向的因果关系。说明郑州市的经济增长并不能由房地产投资的发展来解释,认为郑州市经济的发展大部分由房地产业带动的观点是不对的。郑州市房地产业的未来发展需要正确的宏观政策加以引导。现阶段郑州市房地产投资过热并不是一种好现象,它会影响其他产业的发展。
(二)建议
结论表明郑州市房地产投资额与 GDP之间具有长期的均衡关系,郑州市的房地产投资对经济增长的贡献还是比较显著的。投资过度集中于房地产必定会对经济增长造成不利影响。因为其他产业与房地产业具有很强的关联性。政府应该对房地产投资制定合理的调控政策[6],不能一味地放任房地产的不断开发使其投资过热,也不能对房地产行业进行强制打压。如今郑州市经济发展迅猛,房地产业的发展要适应郑州市宏观经济的发展,必须发挥好房地产投资对郑州市经济增长的推动作用。

