角动量规律在直杆类竞赛题中的应用

郑 金

(凌源市职教中心,辽宁 朝阳 122500)

1 转动定理的应用

对于质量均匀的直杆,或者轻杆与小球的连接体,当由静止状态突然开始转动时,应用质心运动定理和转动定理可求出直杆一端受到作用力的大小和瞬时角加速度的大小以及质心加速度的大小.

图1

例1.如图1所示,一根长度为3L的轻杆上固定质量分别为m1和m2的两个小球,它们的位置把杆的长度均分.用两根竖直的绳子系在杆的两端,使杆沿水平方向且保持平衡状态.试求:当右边绳子被剪断瞬时左边绳子的拉力为多大?

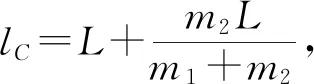
对系统由质心运动定理有

(m1+m2)g-F=(m1+m2)aC，

即 (m1+m2)g-F=(m1+2m2)Lβ.

以加速度瞬心为参考点,由转动定理有

m1gL+m2g·2L=[m1L2+m2(2L)2]β.

解方程得左边绳子的拉力大小为

图2

例2.如图2所示,均质细杆AB的长度为L,质量为m,由两根不可伸长的绳子悬挂,处于水平静止状态.在突然剪断右边绳子的瞬时,求左边绳子拉力的大小和杆的角加速度的大小.

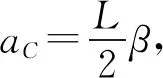
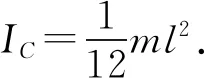
拓展：如果细杆AB开始不是水平的,而是倾斜的,与水平方向的夹角为θ,如图3所示,求左边绳子拉力的大小和杆的角加速度的大小.

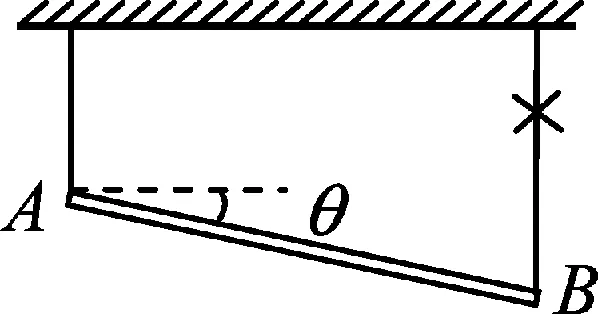
图3

图4

对杆由质心运动定理有mg-F=maC.以质心为参考点,由转动定理有

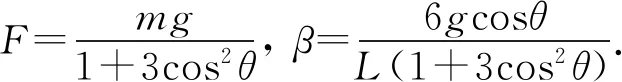
点评:解题难点是确定杆的加速度瞬心,需首先确定A、C两点加速度的方向.在对两个加速度矢量作垂线时,要注意垂线经过两个加速度矢量的起点.在应用转动定理时,若以加速度瞬心为参考点,则有

由于加速度瞬心不在杆上,当以加速度瞬心为参考点时,杆的转动惯量包括两部分,即杆绕质心的转动惯量和质心绕加速度瞬心的转动惯量.

例3.如图5所示,在水平面上有一均质细杆AB的长度为L,质量为m,在竖直平面内与竖直墙面成θ角无初速度下滑,不计接触面的摩擦,求释放瞬时杆两端的加速度为多大?受到的作用力为多大?

图5 图6

解析:杆释放瞬时,角速度为0,则对加速度瞬心而言,法向加速度为0,只有切向加速度,因此转动半径与加速度方向垂直.A点的加速度竖直向下,B点的加速度水平向右,作两个加速度矢量的垂线,可知交点Q为加速度瞬心,如图6所示.杆的质心绕点Q加速转动,同时杆相对于质心C自转,而且相对于点Q的角加速度与相对于点C的角加速度相同，以加速度瞬心为参考点,由转动定理有

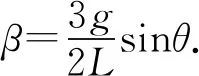
各点绕加速度瞬心的角加速度β相同,由aτ=rβ可知各点的切向加速度跟转动半径成正比,则杆两端A、B的加速度大小分别为

对杆在水平方向由质心运动定理有

FA=maCx,

可得

点评:要注意所求加速度是杆释放瞬时的加速度,因为杆发生运动以后,角速度不为0,则无法找到加速度瞬心.若以质心为参考点,则由转动定理有

2 角动量守恒定律的应用

对于竖直方向质量均匀的直杆,或者轻杆与小球的连接体,当下端受到质点撞击时发生绕轴转动,应用角动量守恒定律和机械能守恒定律可求出直杆转动的瞬时角速度.

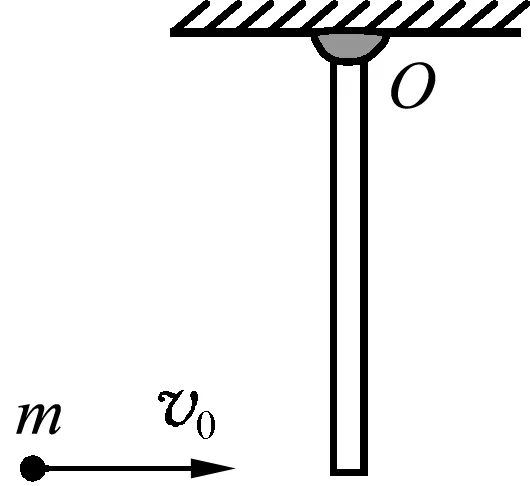
图7

例4.如图7所示,一均匀杆的长度为l,质量为M,可绕上端的水平轴O自由转动,开始时杆处于平衡状态,有一质量为m的子弹以水平速度v0射向杆的下端,嵌入杆内一起绕O点转动,求子弹击中杆后的角速度以及杆的最大摆角.

解析:对于质点与直杆组成的系统,相互撞击力属于内力,当直杆在竖直位置时,系统受到的重力经过水平轴O,则外力的力矩为0.

对系统运用角动量守恒定律，有

可得

设杆的悬点O为重力势能零点,杆的最大摆角为θ,对子弹的圆周运动由机械能守恒定律有

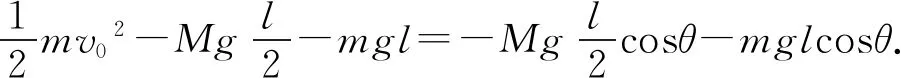
解得

点评:系统的角动量包括质点的角动量和杆的角动量,都相对于同一参考点而言,当子弹刚要撞击到杆之前瞬时,受到的重力的作用线经过参考点,因此重力对子弹的力矩为0,所以系统的角动量守恒.

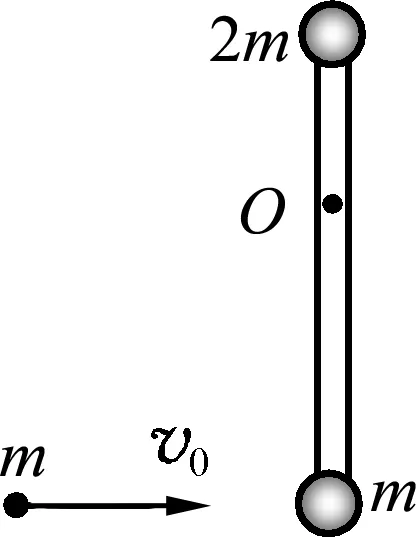
图8

例5.如图8所示,一长度为l的轻杆,两端分别固定质量为m和M=2m的小球,杆可绕水平光滑轴O在竖直平面内自由转动,轴O到下端的距离等于轴O到上端的距离的2倍,杆开始时静止在竖直位置.现有一质量为m的小球以水平速度v0与杆下端的小球做对心碰撞后反弹,碰撞过程没有机械能损失,求碰撞后杆获得的角速度和小球反弹速度的大小.

解析:对于质点与直杆组成的系统,当直杆在竖直位置时,在碰撞瞬时系统受到的重力经过水平轴,则产生的转动力矩为0,因此系统的角动量守恒.设小球反弹速度的大小为v,对系统运用角动量守恒定律有

其中杆球结合体的转动惯量为

对系统运用机械能守恒定律有

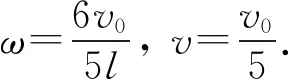
点评:在对系统应用机械能守恒定律时,要注意刚体的动能公式与质点的动能公式不同.若求水平轴对杆的作用力,则对杆竖直向上由牛顿第二定律整体法有

对杆水平向右运用牛顿第二定律整体法有

可得Fy=0,Fx=0.其中角加速度β是由碰撞力矩产生的.

总之,无论应用转动定理还是角动量守恒定律,都需用到转动惯量,因此计算刚体的转动惯量对解题显得至关重要.在应用转动定理时,要首先确定刚体转动的参考点,对于不同的参考点,刚体的转动惯量和受到各力的转动力矩都不同;在应用角动量守恒定律时,要分析系统外力对固定转动轴的力矩是否为0.在刚体上的合外力同时具有两个独立作用效果,即平动效果和转动效果,其中反映转动效果的规律是转动定理,反映平动效果的规律是质心运动定理和牛顿第二定律整体法即广义的牛顿第二定律.