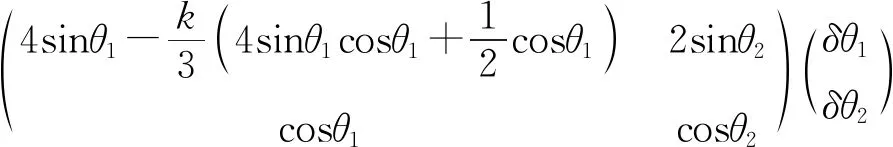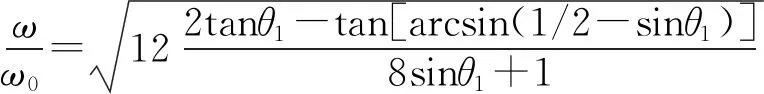正五边形平衡位形能取到吗?

林倩茹 吴静燕 邱为钢

(湖州师范学院理学院, 浙江 湖州 313000)

奥赛物理题选中有这样一道题：5根相同的匀质细杆,用质量密度均可忽略的光滑铰链两两首尾相接连成一个五边形,将其中一个顶点悬挂在天花板下,试求平衡时此五边形的五个顶角.又如在最下边的细杆中点再悬挂一个重物,能否使五个细杆构成一个等腰三角形?原题是用受力分析做的,想在下面加一个向下的力,使得五边形能变为三角形,但没成功.那么有没有向外的力,可以拉伸使得五边形木杆平衡时,变为三角形或正五边形.中学物理所熟悉的这种力是转动参考系下的惯性离心力.本文木杆体系转轴都是对称轴,根据文献[2],这样的匀角速状态可以称为平衡态.我们从能量角度考虑这种平衡态,即体系的重力势能和转动参考系下的离心势能之和,平衡态使得总势能取得极小.我们发现,当用线拎起木杆并使之匀速转动达到平衡时,取适当的角速度,五边形木杆的平衡位形可以取到等腰三角形和正五边形,弥补了文献[1]的遗憾．

先推导以z轴为转轴的转动参考系下,任意放置理想木杆的离心势能与端点坐标的表达式.设木杆两端坐标是(x1,z1)和(x2,z2),长度是L,杆上任意一点的坐标矢量是

r(s)=(1-s)(x1i+z1k)+s(x2i+z2k).

(1)

其中参数s的取值范围是0

(2)

积分计算得到整个杆离心势能为

(3)

sinθ1+sinθ2=1/2.

(4)

把杆端点坐标代入式(3)计算离心势能,再加上重力势能,得到五边形杆总势能为

(5)

五边形杆绕对称轴匀速转动达到平衡时,木杆倾角变化引起总势能的变化为0，

δΦ5=4sinθ1δθ1+2sinθ2δθ2-

(6)

几何约束条件式(4)的变化也是0，

cosθ1δθ1+cosθ2δθ2=0.

(7)

(6)式和(7)式可以写成矩阵形式

(8)

由几何约束条件(4)式,两个角度的变化不是独立的,(8)式存在非零解的必要条件是系数矩阵的行列式为0．计算得到

(9)

当转速参数k=0时,式(9)就退化到文献[1]中的结论.依据式(4),把θ2消去,得到转速与右边第一个木杆倾斜角θ1的关系式

(10)

角速度为0时,倾角θ1为α=0.172242.随着角速度增大,倾角θ1逐渐增大.角速度趋向无穷大时,倾角θ1趋向于π/2,所以倾斜角θ1的取值范围是α<θ1<π/2．

当转动五边形的平衡位形是等腰三角形时,θ1=arcsin(1/4),由(10)式,角速度

当转动五边形的平衡位形是正五边形时,θ1=3π/10,由(10)式,角速度

图1 不同转速下五边形木杆的平衡位形

由此可见,当角速度取合适值时,转动五边形的平衡位形是可以取正五边形的．不同转速下五边形杆的平衡位形如图1所示.