基本不等式求最值中“二定”的解法探究

■侯贝林

方法一：配凑法

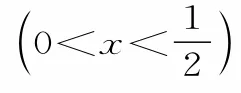
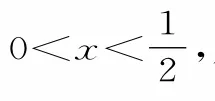
方法点评：对于形如“y=ax(bx+c)+d”类型的问题求最值时,通过配凑项的系数,可达到“积定和最小,和定积最大”的目的。

方法二：分离常数法

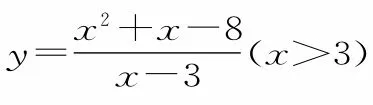
解：因为x＞3,所以x-3＞0。

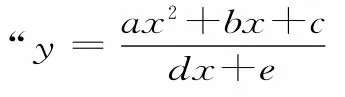
方法三：常数代换法

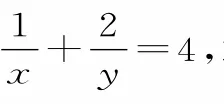
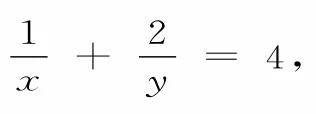
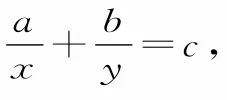
方法四：消元法

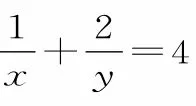
方法点评：对于求解含有两个变量的最值问题时,可以通过消元法把两个变量转化成一个变量,从而更有利于最值的求解。