巧用埃拉托色尼筛选法统计大数据区间内素数算法剖析

周静

摘要：本文从常规算法出发找寻并统计素数，探讨了常规算法在大数据区间找寻并统计素数的低效问题，引出巧妙运用埃拉托色尼筛选法统计大数据区间范围内素数个数方法，并详细剖析该方法算法思路。

关键词：素数;埃拉托色尼筛选法;大数据区间;统计

找寻素数的题目屡见不鲜，总会出现在一些编程教材中。找寻方法都是沿用对素数判断规则，即逐一判断找寻范围内的数，在2至其平方根范围内是否存在因子，如果存在就不是素数，如果不存在就是素数。这种判断方法是沿用素数的定义，也让初学者能轻松理解并掌握控制流程的好方法。但是当区间范围过大以及找寻的数据本身也足够大时，统计速度慢的弊端就会显现出来，完全体现不了现今信息时代所提倡的高效性，怎么来解决对大数据区间素数统计问题呢？

1 常规统计素数方法的低效问题

对于素数统计，总会想到先判断是不是素数，再执行统计。这是思考问题的常规思路。但是判断一个数是不是素数，所采用常规判断素数方法使用“穷举法”排除非素数，穷举出从2至其平方根中是否存在因子，只要存在则排除。当需要判断的数据过大，使用 “穷举法”就会变得很低效。

穷举算法低效在于需要判断的数据可能会在十亿至四十多亿，需要在2至其平方根（即好几万）进行逐一的因子判断，其耗时比预想要大得多，且是在一个大区间内统计，需要进行素数判断的大数据数量众多，造成了统计耗时的成倍增长，运行低效问题也更突出。怎样才能高效实现在大数据区间内的素数统计呢？

2 巧妙统计素数方法的高效原理

在编程语言（C++）中，正整数最大范围可以达到42亿多，如果判断这个数据是否是素数，使用以上常规判断不可取的。如果能有一个空间来描述某个范围内哪些是素数，就可以通过检索这个空间来统计素数的数量。

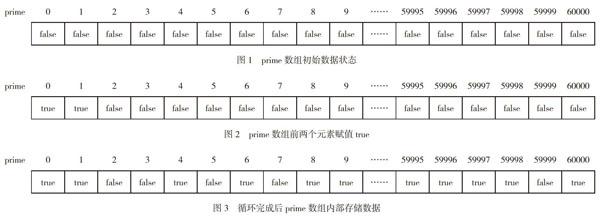
一个区间范围内统计素数只有两种可能，是或不是，使用C++中的布尔值false和true来表示。定义布尔型数组：bool prime[60001];用该数组来描述0-60000范围内哪些是素数，数组元素的默认值为false，即假设其都是素数，prime数组初始化如图1所示：

在0-60000数字中，对于其中的0和1，已知其不是素数，所以为数组元素prime[0]和prime[1]赋值true，表示其不是素数，如图2所示。

从数字2开始判断其是素数，但后面所有是2倍数的数就都不是素数，为其赋值true，这就是埃拉托色尼筛选法的中心思想，算法实现：

for（long i=2;i<=60000;i++）

if（！prime[i]） {

for（long j=i+i;j<=60000;j=j+i）

prime[j]=true;

}

通过以上代码的执行，在prime数组中就记录0至60000哪些是素数（值为false就是素数）的信息。prime数组的表示如图3所示：

这种方法可以将60000内所有非素数置true，是因为只要不是素数就会存在因子，其因子如果也不是素数，可以继续分解，总之一个非素数都可以表达成比它小的素数乘积，即是素数倍数，既然是素数倍数，根据前面的说法，就应该为其赋值为true，标识出其不是素数了。

其高效体现在代码中进入内循环存在条件，且内循环次数随i值的递增，将成i倍递减，与逐一判断是否存在因子的素数判断作为内循环的效率是不可相提并论的。

对大数据区间素数统计该怎么实现呢？在实现代码中使用了prime数组存储布尔值来描述0-60000中哪些是素数。定义数组大小为60000的原因是因为描述素数范围最大数是42亿多，取其平方根是60000多，当得到60000以内的所有素数，再以这些素数为基础，将需要描述的大数据范围内素数倍数都赋值为true，素数统计工作就只需要单层循环检索即可实现。

注意需要了解找寻的大数据范围数量，才能设计一个空间来描述这些数中哪些是素数。可以预想一下需要判断的区间范围，假如是1，000，000，那么需要设计1，000，000的空间来描述该范围内数据是否是素数。即：bool primeMax[1000001];该数组就用来描述这个大数据范围内的数哪些是素数。

描述的数据范围有3种情况：

第一种是当描述数据都在60000以内;

第二种需要描述的数据一部分在60000以内，一部分在60000以外;

第三种是需要描述的数据都在60000以外;

这里用整型变量left表示范围左边界值，用整型变量right表示右边界值，用整型变量count且初始化值為0来累加统计素数量。

（1）第一种情况的统计处理

if（right<=60000）{

for（long i=left;i<=right;i++）

if（！prime[i]）count++;

cout<

}

直接利用prime数组统计完需要描述的区间范围内的素数个数并输出;

（2）第二种情况的统计处理

需要分段处理，首先处理在60000以内的数据，这些数据按第一种情况处理;其次处理不在60000以内的数据，这些数据可以按第三种情况处理。

① 第一段数据（在60000以内的数据）统计处理。

if（left<=60000）{

for（long i=left;i<=60000;i++）

if（！prime[i]）count++;

left=60001;

}

② 第二段数据（在60000以外的数据）统计处理

上面第一段数据统计处理代码实现最后一条语句将60001赋值给left，作用是改变左边界值。这样使得第二段数据可以按下面第三种情况统计处理。

（3）第三种情况的统计处理

需要使用上面定义的primeMax数组来标识60000以外数据是否是素数，该数组如图4所示：

与prime数组类似，先假设所描述60000以外数据它们全部都是素数，再通过检索prime数组中的素数，标识需要描述的60000以外的区间内哪些是素数，为其赋值为true。

其代码实现如下：

long temp;

for（long i=2;i<=60000;i++）{

if（！prime[i]）{

for（unsigned long j=left/i;j<=right/i;j++） {

temp=j*i-left;

if（temp>=0）primeMax[temp]=true;

}

}

}

对于代码中的left/i和right/i作用是使得内循环次数成i倍递减表示方法。因为要为素数的倍数置true，表示其不是素数。

prime中描述了所有60000以内的素数，将在给出的大数据范围内標识出是prime数组中素数倍数的数，将这个表示存储在primeMax数组中。例如，描述60001-70001范围;当i=2时;primeMax数组的表示如图5所示：

代码中需要置true的primeMax数组元素下标temp=j*i-left;该表达式j*i代表需要描述的大数据，该数据是i的倍数。减去left将该数对应到primeMax数组中相应的元素上;

在为primeMax数组元素赋值true时，有一个if条件语句，需要判断temp是否大于等于0，该判断的作用是看描述的大数据j*i，是否在需要描述数据区间范围内;如果temp小于零，代表j*i小于left左边界，即不用描述该数据。当标识完prime数组中所有素数在大数据区间内的倍数标识，即为primeMax数组赋值后，就可以实现区间类素数统计了;前面已经实现了用检索prime数组对60000以内素数统计，现在就对primeMax数组进行检索，统计60000以外的素数量，其实现代码是：

for（long i=0;i<=right-left;i++）

if（！primeMax[i]）count++;

cout<

前面详细讲解利用埃拉托色尼筛选法巧妙统计大数据区间内素数，希望大家能理解和掌握该方法，并能灵活借鉴该方法解决其他类似的问题。

基金项目：本文系2018-2019年度工业和信息化职业教育教学科研课题 “蓝桥杯”技能大赛成果资源在高职教育教学中的实践与应用（编号GS-2019-10-02）; 重庆电子工程职业学院卓越技术技能人才工匠工坊项目“千贝软件工匠工坊”（编号：0319010225 ）的研究成果。

（作者单位：重庆电子工程职业学院）