略谈小学数学教学中的对比
潘少华

【摘要】比较是数学思维和理解的基础。在小学数学教学中,比较常常以对比的形式出现,老师要善于把握教材中安排的这一特点,采取各种对比方式,培养学生多点思考,以达到能够理解知识,掌握知识间的联系与区别。正反对比,通过正反对比可以加深对知识的理解,掌握正运算与逆运算,逐渐培养学生认知的全面发展。辨异对比,即把相近、相似或相关的知识加以对比。同类对比,指通过对同一范畴的事物属性的分析、综合,比较出共同的本质属性。同义对比,即把不一样的两种意义进行对比。顺逆对比,这是指安排学生在由顺到逆,由逆到顺的整体性知识训练中进行对比。一般与特殊对比,数学知识常常既具有一般规律,又存在某种特殊性。整体与部分对比,即在比较中揭示知识的个性,概括共性,从整体认识局部。整体与部分对比,即在比较中揭示知识的个性,概括共性,从整体认识局部。解题思路的对比,复习分数、百分数的过程中,为使学生系统化的掌握所学知识,根据分数、百分数应用题中的数量关系和解题方法进行如下的比较。在对比中找结论,二年级“有余数的除法”教学中,运用比较进行设疑,使学生能积极开动脑筋,参与探索。解题方法“多变”中的比较。
【关键词】小学数学 教学中 对比
【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089(2019)28-0126-02
比较是数学思维和理解的基础。在小学数学教学中,比较常常以对比的形式出现,老师要善于把握教材中安排的这一特点,采取各种对比方式,培养学生多点思考,以达到能够理解知识,掌握知识間的联系与区别。在多年的教学中,使自己积累了以下一些对比方法的粗浅认识。
一、正反对比
通过正反对比可以加深对知识的理解,掌握正运算与逆运算,逐渐培养学生认知的全面发展。
如:四年级上册乘法分配律的正反运用的教学中,我用“分”[28×(15+125)]和“取”[32×17+67×17+67]的生活故事加以描述,使学生掌握乘法分配律可以正用(分),也可以反用(取),即灵活的运用了乘法分配律,又避免了以前对乘法分配律的死搬硬套,学生也易于掌握。此外,加与减,乘与除,正比例与反比例等都是正反对比。
二、辨异对比
辨异对比,即把相近、相似或相关的知识加以对比。如2a与a2、求比值与化简比、约数与倍数等,通过对易混淆知识的对比,不仅掌握了知识间的差异,能准确区别各自内涵,而且可以把握知识间的联系,特别对于不善观察、思考、粗心的学生可帮助其提高认知和理解能力,更有效的加深对不同知识的掌握和运用,发展学生的实践技能。
三、同类对比
同类对比,指通过对同一范畴的事物属性的分析、综合,比较出共同的本质属性,从而实现抽象概括,培养学生的乐于思考,善于发现,勤于总结的良好习惯,激发思维能力的提高。如学生学过约分和通分后,一般情况理解往往停留在“两种过程”“两种方法”的浅层认识上,若适时组织对比引导,让学生知道两者都是应用“分数的基本性质”——“约分是分子、分母同时缩小相同的倍数”,“通分则是分子、分母同时扩大相同的倍数”。引导学生的思维向深层次发展,让学生明白原来数学知识有这样密切的联系,自然而然的激发了学生学习数学的兴趣。
四、同义对比
同义对比,即把不一样的两种意义进行对比,如:(1)有一段铁丝长360米,用去四分之三,用去多少米?(2)有一段铁丝长360米,用去四分之三。还剩多少米?
五、顺逆对比
顺逆对比,这是指安排学生在由顺到逆,由逆到顺的整体性知识训练中进行对比。例如:
(1)加工3000个零件,平均每天做375个,做了6天后还剩多少个?
(2)加工3000个零件,平均每天做375个,做了几天后还剩750个?
(3)加工3000个零件,做了6天后还剩750个,平均每天做多少个?
通过组织顺逆题组对比练习,使学生思维方式不断变化,正向、逆向都能思考,激发学生学习数学的兴趣,启迪探究解决问题的思路都有重要意义。
六、一般与特殊对比
数学知识常常既具有一般规律,又存在某种特殊性。例如:在学生认识了许多图形(长方形、正方形、平行四边形、三角形、梯形)时,启发学生想象,如果把梯形的上底向一端逐渐缩短,一直缩到这个端点,这时梯形的上底为0。那么梯形就变成了三角形;如果把梯形较短的一条底边像一边延伸到和较长的底边相等时梯形变成了平行四边形;如果平行四边形有一个内角是直角,这时平行四边形就变成了长方形;当长方形的长与宽相等时,它就成为正方形。(如图)
顺势引导,启迪学生发现梯形的面积公式适用于这些平面图形面积的计算。通过数学知识的“一般”与“特殊”的比较,能使学生感性上认识事物的普遍性和特殊性的辩证关系。
七、整体与部分对比
整体与部分对比,即在比较中揭示知识的个性,概括共性,从整体认识局部。如:整数与自然数的认识,它们实际是整体与部分的关系。这种在整体与部分的比较中学习,有利于学生认识数学知识的内在联系与特征,从而形成良好的认知结构。
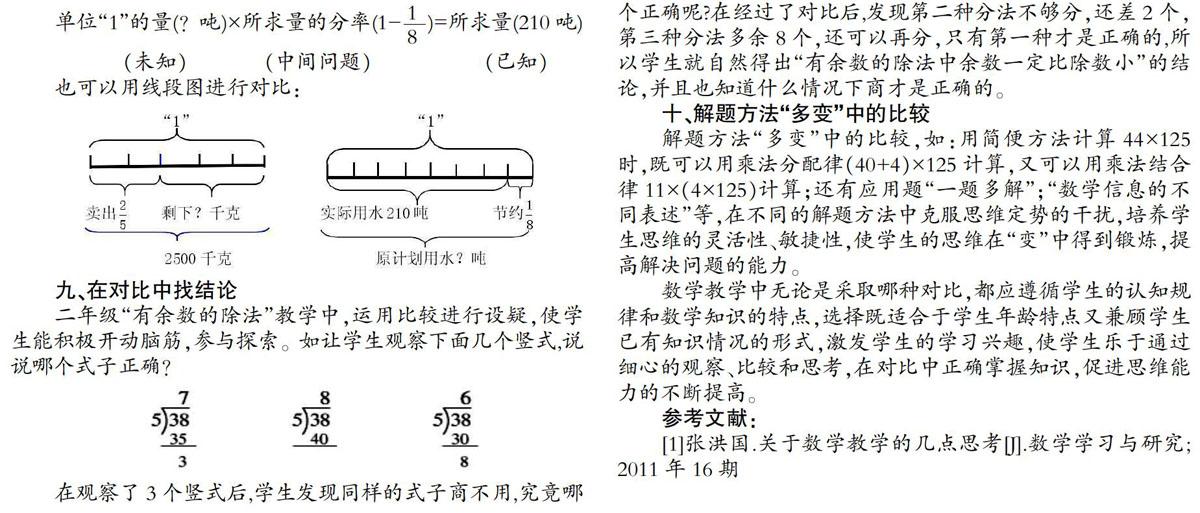
八、解题思路的对比
复习分数、百分数的过程中,为使学生系统化的掌握所学知识,根据分数、百分数应用题中的数量关系和解题方法进行如下的比较。
(1)水果批发公司有水果2500千克,卖出2/5,还剩下多少千克?
(2)学校九月份用水210吨,比原计划节约了1/8。原计划用水多少吨?
九、在对比中找结论
二年级“有余数的除法”教学中,运用比较进行设疑,使学生能积极开动脑筋,参与探索。如让学生观察下面几个竖式,说说哪个式子正确?
在观察了3个竖式后,学生发现同样的式子商不用,究竟哪个正确呢?在经过了对比后,发现第二种分法不够分,还差2个,第三种分法多余8个,还可以再分,只有第一种才是正确的,所以学生就自然得出“有余数的除法中余数一定比除数小”的结论,并且也知道什么情况下商才是正确的。
十、解题方法“多变”中的比较
解题方法“多变”中的比较,如:用简便方法计算44×125时,既可以用乘法分配律(40+4)×125计算,又可以用乘法结合律11×(4×125)计算;还有应用题“一题多解”;“数学信息的不同表述”等,在不同的解题方法中克服思维定势的干扰,培养学生思维的灵活性、敏捷性,使学生的思维在“变”中得到锻炼,提高解决问题的能力。
数学教学中无论是采取哪种对比,都应遵循学生的认知规律和数学知识的特点,选择既适合于学生年龄特点又兼顾学生已有知识情况的形式,激发学生的学习兴趣,使学生乐于通过细心的观察、比较和思考,在对比中正确掌握知识,促进思维能力的不断提高。
参考文献:
[1]张洪国.关于数学教学的几点思考[J].数学学习与研究;2011年16期

