非线性矩阵方程中心对称解的牛顿-MCG算法

陈世军

( 福建工程学院 应用技术学院， 福建 福州 350001 )

0 引言

在控制理论、随机滤波和超分辨率图像恢复等领域，会遇到形如

X+E1X-1F1+E2X-2F2+E3X-3F3=G

(1)

的含有未知矩阵高次逆幂的非线性矩阵方程[1-4]，其中Ei，Fi，G，X∈Rn×n(i=1,2,3).文献[5-8]研究了牛顿算法在求解线性方程和非线性方程中的应用.程可欣等[8]研究了方程(1)的特例X-ATX-1A=Q的牛顿迭代解法，证明了牛顿迭代方法产生的矩阵序列包含在确定的闭球内，且该矩阵序列收敛到闭球内唯一的矩阵方程的解.张肖肖等[9]给出了方程(1)对称解的双迭代算法，其先用牛顿算法求出等价的线性矩阵方程的对称解，然后再采用修正共轭梯度算法(MCG算法)求出由牛顿算法每一步迭代计算导出的线性方程的对称解或对称最小二乘解.目前，对于方程(1)的中心对称解的研究还未见报道.为此，本文基于文献[9]的算法原理，将牛顿-MCG算法推广到求解方程(1)的中心对称解上.

1 求方程(1)中心对称解的牛顿算法

定义1划分n阶单位矩阵I=(e1,e2,…,en)， 称Sn=(en,en-1,…,e1)为n阶次单位矩阵.若X∈Rn×n满足SnXSn=X， 称X为中心对称矩阵，用CSRn×n表示中心对称矩阵集合.

基于文献[9]的算法原理，建立求非线性矩阵方程(1)中心对称解的牛顿-MCG算法.令X=X-1，则方程(1)可以改写为

X-1+E1XF1+E2X2F2+E3X3F3=G.

(2)

首先用牛顿算法求方程(2)的中心对称解，然后采用MCG算法求由牛顿算法每一步迭代计算导出的线性矩阵方程的中心对称解或中心对称最小二乘解，以此建立求方程(2)中心对称解的牛顿-MCG算法.

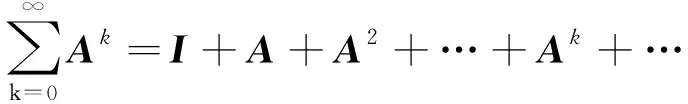
根据定义2可知，当-X-1Y的谱半径小于1时，有

引入下列矩阵函数：

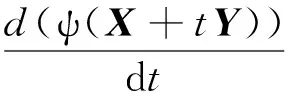
又因为

ψ(X+Y)=(X+Y)-1+E1(X+Y)F1+E2(X+Y)2F2+E3(X+Y)3F3-G=

E2YXF2+E3X3F3+E3X2YF3+E3XYXF3+E3XY2F3+E3YX2F3+E3YXYF3+

E3Y2XF3+E3Y3F3-G，

容易导出ψ(X+Y)=ψ(X)+φX(Y)+γX(Y).这里φX(Y)是ψ(X)在“点X”沿着“方向Y”的Frechet导数.

引理1[9]设X∈CSRn×n是方程(1)的近似解，则求方程(1)的解X等价于求校正值Y∈CSRn×n使得ψ(X+Y)=O， 并可以线性化为求Y∈CSRn×n, 使得

φX(Y)=-ψ(X).

(3)

参考文献[9]的算法原理,通过修改某些矩阵的类型，建立求方程(1)中心对称解的牛顿算法，该算法的具体步骤如下：

第1步 给定初始矩阵X(1)∈CSRn×n， 置k∶=1.

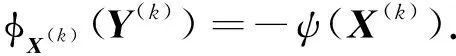
第3步 计算X(k+1)=X(k)+Y(k)， 置k∶=k+1， 转第2步.

对于牛顿算法有如下的收敛性结论：假设X*是方程(1)的单根，且初始矩阵X(1)充分接近X*，那么牛顿算法确定的矩阵序列{X(k)}二次收敛于X*.

2 求线性矩阵方程(3)中心对称解的MCG算法

记A1=E1，B1=F1，A2=E2X，B2=F2，A3=E2，B3=XF2，A4=E3X，B4=XF3，A5=E3X2，B5=F3，A6=E3，B6=X2F3,A7=-X-1，B7=X-1，F=-(X-1+E1XF1+E2X2F2+E3X3F3-G).考虑方程(3)的一般形式：

(4)

其中Ai,Bi,Ci,Di,F∈Rn×n(i=1,2,…,7).本文解决下面两个问题：

问题Ⅰ 设方程(4)有中心对称解，求Y∈CSRn×n， 使Y满足方程(4).

问题Ⅱ 设方程(4)无中心对称解，求Y∈CSRn×n， 使

(5)

当方程(4)有中心对称解时，称问题Ⅰ相容；否则,称问题Ⅰ不相容.

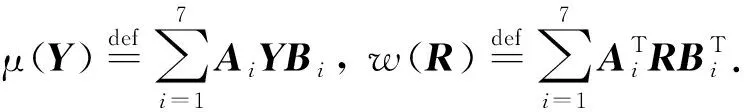
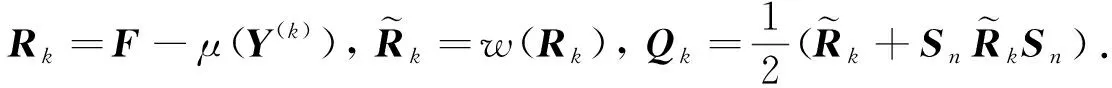
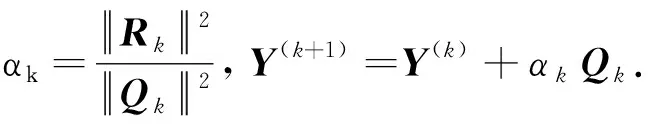
第4步 置k∶=k+1， 转第2步.

由以上步骤易见，算法1中的矩阵Y(k),Qk∈CSRn×n.下面给出算法1的基本性质，算法1在有限步计算之后停止,具体证明可参考文献[11].

引理2对任意的A∈Rn×n，Y∈CSRn×n均有tr((A+SnASn)TY)=2tr(ATY).

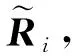
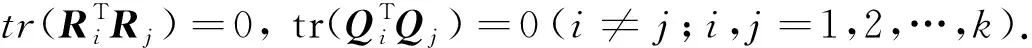
定理1设问题Ⅰ相容，则对任意的初始矩阵Y(1)∈CSRn×n，算法1可在有限步计算后求得问题Ⅰ的一组解.问题Ⅰ不相容的充要条件是存在正整数k，使得由算法1得到的Rk≠O而Qk=O.

定理2设问题Ⅰ相容，选取初始矩阵Y(1)∈CSRn×n满足

则算法1可在有限步计算后得到问题Ⅰ的唯一极小范数解，即方程(4)的唯一极小范数解.

3 求解问题Ⅱ的MCG算法

根据定理1，在算法1中当Rk≠O而Qk=O时，算法1中断.这表明线性方程(4)没有中心对称解,因此需要求解问题Ⅱ，即求线性方程(4)的中心对称最小二乘解.下面通过构造等价的线性矩阵方程组，将求矩阵方程(4)中心对称最小二乘解问题转化为求等价的正规方程中心对称解问题；然后参照算法1，建立求矩阵方程(4)中心对称最小二乘解的迭代算法.

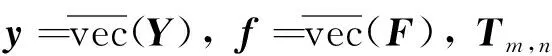
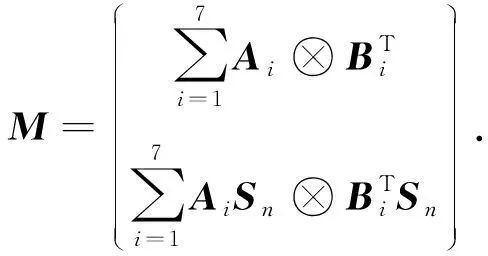
定理3求解问题Ⅱ等价于求线性矩阵方程

f(Y)=N

(6)

的中心对称解，并且方程(6)一定有中心对称解.

证明求解问题Ⅱ等价于求Y∈CSRn×n， 使得

(7)

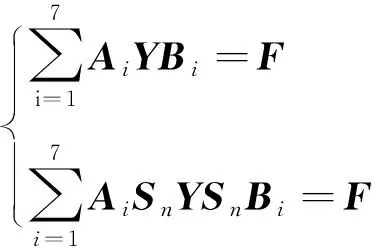
参照算法1以及MCG算法的基本原理，建立求矩阵方程(6)中心对称解的算法，即求解问题Ⅱ的MCG算法.求解问题Ⅱ的MCG算法(算法2)的具体步骤如下：

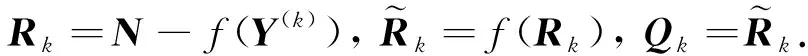
第4步 置k∶=k+1， 转第2步.

由以上步骤易见，算法2中的矩阵Y(k),Qk∈CSRn×n.对于算法2有类似于算法1的收敛定理.

定理4对任意的初始矩阵Y(1)∈CSRn×n， 算法2可在有限步计算后求得问题Ⅱ的一组解，即矩阵方程(6)的中心对称最小二乘解.若取初始矩阵Y(1)满足Y(1)=f(H) (∀H∈CSRn×n)， 则算法2可在有限步计算后得到矩阵方程(6)的唯一极小范数中心对称解.

4 数值算例

用上述建立的算法1和算法2求矩阵方程(1)的一组中心对称解和中心对称最小二乘解.取方程(1)的系数矩阵均为块对角矩阵，且均为5n阶方阵.系数矩阵、初始矩阵和终止准则如下：

A为三对角矩阵，其中ai,i=3，ai,i -1=2,ai -1,i=2 (i=1,2,…,5n), 其余元素均为0;

E1=-AT，F1=A，E2=O，F2=O，E3=O，

F3=O，G=I，X1=I，ε=10-9(终止准则).

选取初始矩阵Y1=2I， 按照算法1和算法2可求得矩阵方程(1)的一组中心对称解，结果见表1.表1中， 5n为系数矩阵的阶数，t为计算时间，k1为算法1的迭代次数，k12为算法1的中断次数，k2为算法2的迭代次数，error为实际误差的范数.

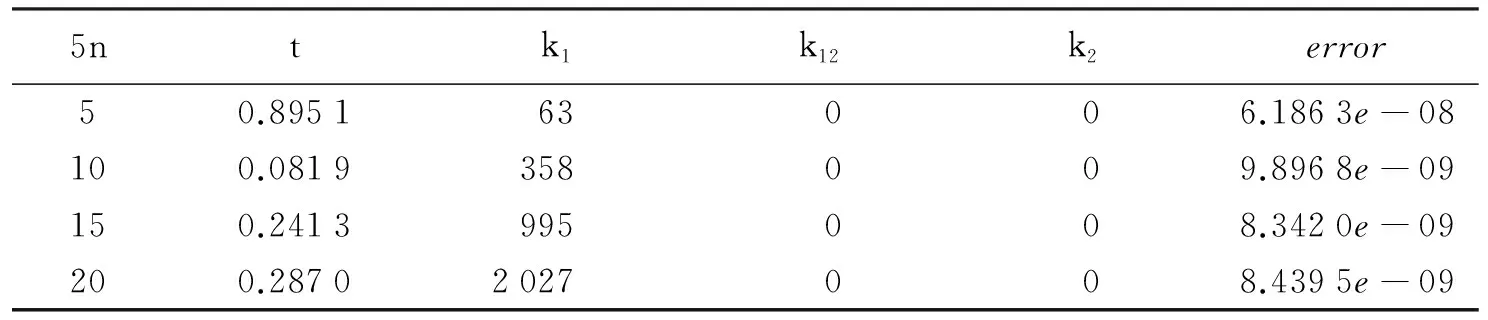
表1 矩阵方程(1)的计算结果

从表1可以看出，运用算法1和算法2求解方程(1)是有效的.当算法1中断时，可以通过算法2计算方程(1)的中心对称矩阵最小二乘解.若修改算法1中矩阵Qk的类型，则可以建立求其他特殊矩阵解的迭代算法.