动能定理不依赖惯性参考系选取的证明

苏石磊， 闫磊磊， 潘志峰

( 郑州大学 物理工程学院, 郑州 河南 450001 )

0 引言

牛顿第二定律指出：“质点的运动状态发生改变的前提是受到外力的作用，获得加速度.”牛顿第二定律描述的是力对物体的瞬时作用，但在很多实际情况时，作用在物体上的力会持续一段时间，移动一定的位移.力在时间上的累积作用FΔt对物体运动状态的影响体现在动量定理[1].力在空间上的累计作用F·Δr对物体运动状态的影响由动能定理体现[2].目前，大多数大学物理教材[1-4]在介绍动能定理的特点时，仅将其简单地描述为：“动能定理不依赖于惯性系的选取”，并没有给出严格的证明，这使得学生难以真正掌握动能定理，影响后续大学物理知识的学习.针对这一问题，本文利用基本惯性参考系和运动惯性参考系来证明动能定理不依赖于惯性参考系的选取，以此加深学生对动能定理的理解，帮助学生提高创新思维和发散思维[5-8].

1 预备知识

1) 动量定理.牛顿第二定律为：

(1)

式中F代表作用在系统上的合外力，p=mv为系统的动量，t为时间，m为系统质量.对公式(1)变形并积分可得：

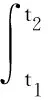
(2)

式中p1为系统在t1时刻的动量，p2为系统在t2时刻的动量.公式(2)即为动量定理的积分形式,其物理意义为：在给定的时间间隔内，外力作用在质点上的冲量，等于质点在此时间内动量的增量.如果力为恒力，则积分变为力与时间的乘积.

2) 动能定理.如图1所示，质量为m的质点在合力F的作用下，自A点沿曲线移动到B点.质点在点A和点B的速率分别为v1和v2.设作用在位移元dr上的合力F与dr之间的夹角为θ， 则合力对质点所做的元功为

dW=F·dr=Fcosθ|dr|.

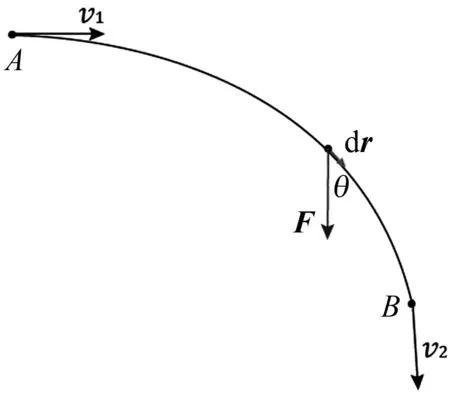
图1 动能定理示意图

由牛顿第二定律及切向加速度的定义可得：

因为ds=vdt， 得dW=mvdv.再对dW=mvdv进行积分可得动能定理：

(3)

3) 相对运动.如图2所示，考虑2个参考系，一个为oxy坐标系(S系)，另一个为o′x′y′ 坐标系(S′系).初始时2个参考系重合.本文研究的质点，在S系中的位置以P表示，在S′系中的位置用P′表示.在Δt时间内，S′系相对于基本参考系以速度u沿y轴运动.在S系中，质点从P点运动到Q点，其位矢为Δr.在S′系中，质点从P′点运动到Q点，其位矢为Δr′.这些矢量之间满足以下关系[3]：

(4)

当取Δt→0， 可得

v=v′+u,

(5)

其中v为质点相对于基本参考系的速度，v′为质点相对于运动参考系的速度.

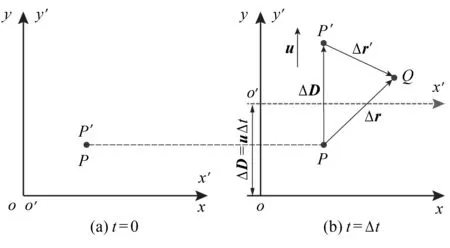
图2 质点在相对作匀速直线运动的两个惯性参考系中的力学量

2 动能定理形式不依赖于参考系选取的证明

首先证明动量定理形式不依赖于参考系的选取，然后按照类似的思想去证明动能定理形式不依赖于参考系的选取.

假设运动惯性参考系S′相对运动基本惯性参考系S沿某一固定方向以速度u运动，质点受一恒力F作用，作用时间为Δt.则在S系中，动量定理的表达形式为:

FΔt=mv2-mv1，

(6)

其中t为作用时间，m为质点质量，v1为初速度，v2为末速度.公式(6)可以变形为

FΔt=m(v2-u)-m(v1-u).

由相对运动的公式(5)可得：

FΔt=mv′2-mv′1.

(7)

从公式 (6) 和公式 (7) 可以看出，动量定理形式不依赖于参考系的选取.

假设质点在基本惯性参考系中移动的位移矢量为Δr， 在运动惯性参考系中移动的位移矢量为Δr′， 运动惯性参考系相对于基本惯性参考系的移动速度为u.在基本惯性参考系中，质点的初始速度和末速度分别为v1和v2； 在运动惯性参考系中，质点的初始速度和末速度分别为v′1和v′2.在基本惯性参考系中，质点的动能定理可以表示为:

(8)

在动量定理式(6)两侧右端同时点乘u可得：

F·uΔt=mv2·u-mv1·u.

(9)

公式 (8)减公式(9),得：

(10)

公式 (10) 可变形为

(11)

利用公式(a-b)2=a2-a·b-b·a+b2简化公式(11)，同时考虑标量积特点(a·b=b·a)及相对运动公式 (4)和(5)后，公式(11)可变形为

(12)

通过对比公式(8)和公式(12)可知，质点动能定理在不同参考系下的形式是一致的.上述证明过程是在恒力的作用下，对于变力的情况，也可以利用类似的方法证明.

3 结论

本文利用基本惯性参考系中的动能定理和矢量运算法则，求解出运动惯性参考系中的动能定理，即证明了动能定理形式不依赖于参考系的选取.该证明不仅有利于学生掌握动能定理和提高学生分析问题、解决问题的能力，而且有利于培养学生的探究精神和创新思维.