基于SDF及K-M eans三维模型一致性分割算法∗

贾 晖 张建刚

（1.西安邮电大学计算机学院 西安 710121）（2.西安热工研究院有限公司电站信息及监控技术部 西安 710032）

1 引言

近年来，由于三维扫描和三维建模技术的大量应用，三维模型的数量呈指数级增长。使得基于三维网格的几何处理成为重要研究热点。特别是快速建模、模型理解和三维数字重建。三维模型分割就是以上热点问题的基础研究方向。三维模型分割是根据模型的几何特征将模型分解成为一组数目有限、各自具有简单形状意义且各自连通的子部分［1］。

模型集一致性分割是指同时对一组形状相关但姿态有差异的三维模型集进行分割，得到语义相关分割结果的分割方法［2］。一致性分割算法能得到同尺度的分割结果，算法具有实用性，被广泛应用于快速建模［3～5］及三维数字模型重建［6～8］。

现有的分割方法中，文献［9～11］采用离散曲率作为特征对三维模型进行分割。由于曲率是曲面的几何性质，由于噪声的存在，三角网格顶点的离散曲率计算精度不够，在很大程度上影响网格分割算法效果。

文献［12］采用平均测地距离（AGD）对模型进行分割。AGD特征具有尺度不变性，能很好地衡量模型中每一点的孤立程度。然而该特征无法精确描述模型的部位特征，特别是对一个具有相似形状的模型集。

绝大多数算法都是采用了聚类的方法。而聚类算法可分为有监督聚类算法和无监督聚类算法两类。算法中所采用的形状描述子大多都基于模型的表面特征如曲率、法线方向、平均测地距离等特征来描述模型之间的形状特征并对模型集进行分割。有监督的算法能获得较好的分割结果，然而设计训练集需要大量的时间，而且需要大量的人工参与。而模型表面特征如曲率，测地距离，法线方向等容易因为类似模型的不同姿态的变化而发生显著变化，使其丧失模型间形状可比性。因而采用表面特征不利于在具有形状相似而姿态存在差异的模型集上进行一致性分割。

本文提出一种采用形状直径函数［13］（SDF）特征的无监督模型集进行一致性分割算法。SDF特征不是模型的表面特征而是基于模型体特征的形状特征。它具有当模型姿态发生变形时，同一部位的特征值基本保持不变的特点。非常适用于具有不同姿态但形状相似的模型之间的部位相似性计算。首先提取模型集中各个模型的SDF特征，其次K-Means算法对三维模型集中的各个模型进行聚类分割。为了提高K-Means算法的实现效率，用显著特征点作为初始迭代的中心。实验证明将本文算法应用于COSEG［14］模型集中能较高效、准确地实现模型集的一致性分割。

2 形状直径函数（SDF）

形状直径函数（SDF）最早由Shapira在研究模型分割和骨架提取时提出。

SDF特征的计算方法如下:对于三角面片上的每一个顶点，从该顶点以法线反方向为轴做圆锥。在圆锥内部，从顶点向三角面片的另一侧发射射线。如图1所示。对于每一条射线计算发出顶点到与另一侧面片交点之间的射线长度。设ri是第i条射线的长度，且i=[1…n]。射线的平均长度为，射 线 长 度 标 准 差 为 σ=。定义标准差的有效范围为。如果 rj∈range ，则保留，否则将该射线删除。对于每一条范围内的射线 rj∈range，定义权重 ωj，且 ωj=1/αj，αj是 rj与圆锥轴的夹角。顶点的SDF值计算公式为

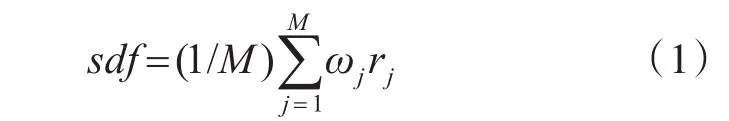
M是落在range范围内的射线的数量，取射线与圆锥夹角的倒数作为参数是希望射线在每个单位面积内均匀出现。大的夹角出现的频率较高，所以具有较小的权重。每个三角面片的SDF值的计算方法是首先使用式（1）计算各面片重心点的SDF值，其次使用式（2）进行归一化，获得面的SDF值，其中α为归一化参数。

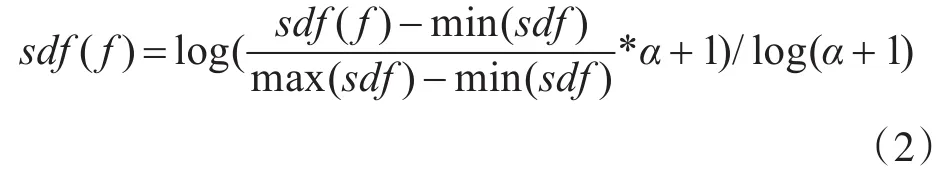
SDF值在模型的变形中基本保持不变，因为SDF的定义跟模型的体相关而与表面特征无关。同样，不同模型的类似部位同样也有着相似的SDF值，因为类似部位具有相似的体特征。SDF特征对平移、旋转、简化、姿态变化具有很好的鲁棒性，可使用SDF值对同一模型的不同变形以及相似的模型进行一致性分割。

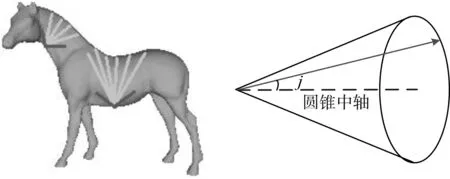
图1 计算SDF特征值

3 基于SDF的K-M eans分割算法

本文采用K-Means算法对模型进行聚类分割。K-Means算法具有实现简单，且算法的时间复杂度接近于线性的优点。但是K-Means算法聚类中心的选取是随机选取的，而聚类中心对分割结果及迭代次数具有巨大影响。本文首先计算模型的显著特征点，用显著特征点作为分割的聚类中心，求得模型集的分割结果。

3.1 显著特征点

定义模型距离重心最远的点为显著特征点。代表了分割的部位。求取显著特征点的好处是能大大减少K-Means算法的迭代次数，且特征点数由人工定义，提高分割的准确性。

定义显著特征点集为S，具体的计算步骤为

STEP1:求模型集中每个模型的重心点坐标v(x,y,z)。

STEP2:定义显著特征点数c，特征点集S。

STEP3:对于每个三维模型M，求对偶图形M'，所有分割的计算在M'上进行。将对面的分割转化为对顶点的分割。计算v1=m in(D(vi,v))，其中vi为M'中各点，v1为重心点v距离三维模型各点欧式距离最近顶点，代表三维模型的主体部分。

STEP4:计算d(vi,v1)，求点云中其它点到v1的测地距离，取距离最大的前c-1个，加入到特征点集S中，代表三维模型的部位划分部分。图2为各模型的特征点结算结果示意图。

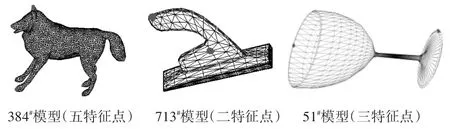
图2 特征点计算

3.2 K-M eans算法

输入:待分割三维模型M'，特征点集S，聚类数c。

输出:c组聚类。

1）根据式（2）计算 M'中所有面的SDF特征值F={f1,f2,…fm}。m为三角网格的面片数。

2）以特征点集S中的c个顶点对应的面片作为初始聚类中心:O1(1)，O2(1)，…Oc(1)。其中Oi(k)代表在第k次迭代中第i个聚类中心。

3）计算F中各面片SDF特征值与聚类中心SDF特征值的欧式距离，将每个面片归到最近的类中。

4）计算Oi(k)中所有面片SDF特征平均值，将得到的平均值作为这一类新的聚类中心Oi(k+1)。

5）对于所有的 i=1…c，如果 Oi(k)=Oi(k+1)则输出O1(k)，O2(k)，…Oc(k)为聚类中心代表的划分结果，否则k=k+1转STEP3继续执行。

4 实验结果与分析

在Windows上，采用分割数据集（COSEG）进行实验，算法运行环境为Intel Core i3 3.3GHz CPU，4 GB内存。开发平台为MicrosoftVisual Studio 2010，图形库为OpenGL。COSEG数据集是具有多个大类的三维模型集，每个模型集中又有若干个类似的三维模型。

以统计数据来评价分割的好坏，文献［11］定义了面片划分的准确程度的算法，用划分正确面积与模型总面积的比值来计算。式（3）中l是分割算法得到面片的划分，t是面片真实的划分。由ai代表面片 i的面积，δ(li=ti)的取值是当 li=ti时δ(li=ti)=1，即为面片划分正确的次数。

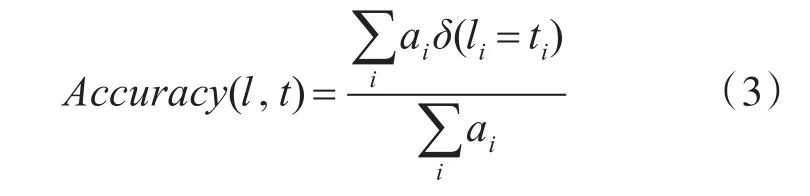
对模型集中每一个模型采用本文算法进行一致性分割，计算算法对每个模型划分的准确程度，并用模型数量进行平均，得到了算法对整个模型集的面片平均划分准确率。表1为本文算法应用式（3）计算的模型分割准确率的实验数据。从数据显示算法的面片平均划分准确率较高，能够实现模型集上的一致性分割。图3为本文算法对三维模型的分割结果。

从图3可以看出，分割部位具有一定的对应关系。四足动物五分割中，模型被分为头、四足、身子、尾巴和耳朵。酒杯模型三分割中，模型被分为底座、手柄和杯口。工具模型的二分割中，模型被分为手柄和主体。台灯模型三分割中，模型被分为灯、连接件和底座。由图3可以得出，本文算法能够对具有类似形状特征的模型集进行一致性分割。有些部位的分割由于特征的计算误差产生错分，分割准确率见表1所示。

图3 本文算法的分割结果

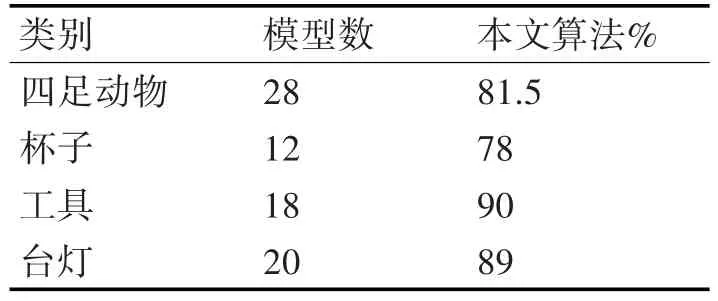
表1 实验模型集平均面片划分准确率

将本文算法与文献［9］、文献［12］和文献［15］方法进行对比。文献［15］采用传统K-Means聚类算法进行分割。传统K-Means算法简单、执行速度快，但是聚类中心随机选择，一旦初始聚类中心选择不好则迭代时间长，很难达到理想的分割效果。

最常用的表面特征就是曲率特征和平均测地距离特征。文献［9］采用曲率特征进行分割。曲率能较好地反应三维曲面在局部的弯曲程度，但离散曲率的计算容易受到噪声的干扰，且类似形状模型若有姿态的变化则会造成曲率的不同，不利于产生一致性分割结果。文献［12］提出的AGD特征不能很好的实现完整部位的分割。图4为本文算法的分割结果与文献［9］算法和文献［12］算法的分割结果对比。从比较结果来看，本文算法的一致性分割结果更为准确。

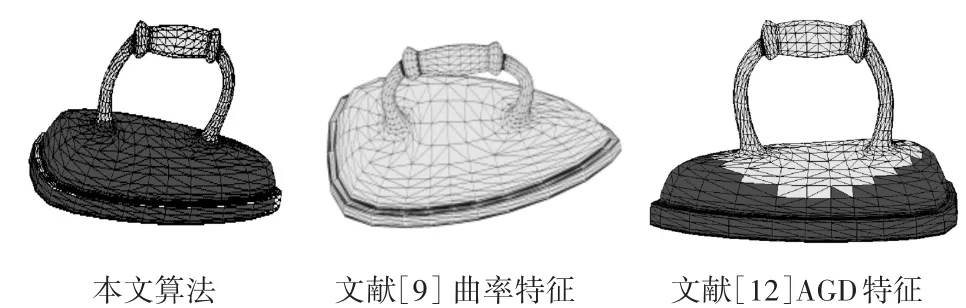
图4 本文算法与其它方法的结果比较

5 结语

本文一致性分割算法共三个步骤，首先对网格模型中每一个三角面片计算SDF特征，其次选取显著特征点作为K-Means算法的聚类迭代中心，最后对特征进行K-Means聚类。实验结果证明本文算法能够对拥有多个具有类似形状模型的模型集进行有意义的一致性分割，且面片平均划分准确率较好。

另外，工作中如下两点还需要继续研究:首先分割部位的数量需要人为设定，还不能实现完全无监督的模型分割；其次SDF特征为体特征，但对于同一模型具有类似体特征的部位不能很好地区分。未来的主要研究方向为采用多特征来提高分割的准确性，并实现必要的特征优化。