含风电发电系统的负荷优化调度灵活性研究∗

宋 弦 姚 刚 伍士红 贺先强 张 旭

（贵州电网有限责任公司电力调度控制中心 贵阳 550000）

1 引言

电力系统灵活性是指电力系统响应系统负荷波动以及电源出力变化而进行调节的能力，系统灵活性侧重于电源随着负荷波动进行追踪调节的能力［1］。而当系统中接入风电等可再生能源后，由于风电的不确定性和波动性，导致系统对负荷波动的跟踪能力变为了系统对负荷和风电所造成更复杂的双重波动影响的跟踪能力，这就需要系统中有足够的灵活性资源来应对这些波动［2～4］。因此，对电力系统灵活性进行相关研究，有助于接纳更多的风电出力，实现电力系统的低碳运行。

文献［5］提出灵活性资源包括可由常规火电机组、快速启停机组、储能设备以及负荷需求响应，通过调用灵活性资源而降低不必要的削负荷情况，同时负荷需求响应可以平滑负荷曲线，降低负荷波动。文献［6］提及了负荷和风速的不确定性对电力系统灵活性所产生的影响，考虑了风功率预测误差的时间相关性，提出了相关指标计算的方法和流程，分析了负荷不确定性和风速不确定性对灵活性影响的不同机理，并研究风电接入容量等不同影响因素对系统灵活性指标产生定量的影响。文献［7］则考虑由于风电渗透率的提高而导致的不确定性，从电力市场的角度出发，考虑系统运行时灵活性所带来的正负电价，建立在电力市场下的灵活性评估模型。文献［8］在提供系统灵活性的方面，分析了机组规划和市场运行的不同表现，从机组规划的角度出发，考虑提供高灵活性机组的投资和运行成本；从电力市场的角度出发，考虑不同运行决策对总成本所带来的影响。

然而以上对电力系统灵活性从不同角度进行描述的过程中，均没有考虑多风电场之间的风速相关性对系统灵活性的影响。本文计及多风电场风速相关性，采用ARMA时移风速方法，生成符合实际相关性要求的多风电场风速数据，提出了一种较为简单的灵活性评价方法，定义了灵活性评价指标，建立了计及多风电场风速相关性的灵活性评估模型。

2 风电场出力模型

2.1 计及相关性的时移ARM A风速模型

风电场的风速序列具有时序自相关性，因此可通过历史风速进行风速模拟。本文采用自回归滑动平均方法［9］生成符合实际自相关性的风速序列。

根据历史数据确定出自回归滑动平均模型ARMA(n,m)，相关表达式如下:

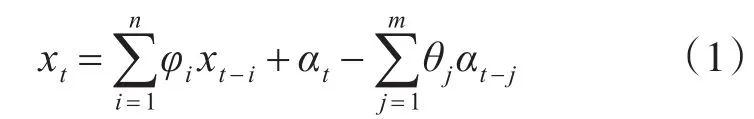
其中，φi表示相应自回归参数；θj表示滑动平均参数；xt为标准化后的风速时间序列；表示一个正态白噪声过程，正态分布的方差为。可以据此建立起标准化的模拟风速序列，接着还原而得到模拟风速序列。

其中，σv为历史每小时风速标准差；Vt表示还原后的预测风速序列。

本文中采用皮尔逊相关系数来表征两个风电场风速之间的相关性［10］。随机变量x和 y的皮尔逊相关系数为

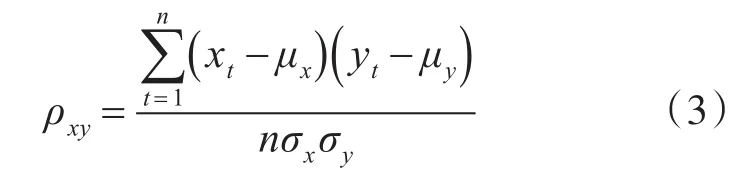
式中，μx和 μy是两个时间序列的均值，σx和 σy是两个时间序列的标准差，n是时间序列所包含的数据项数。

ARMA模型中的白噪声序列极大地影响了不同ARMA模拟风速之间相关性，所以根据I，II两地区历史风速数据以及式（1），首先使用相同的白噪声过程αt生成I，II地区风速时间序列和，保持不变，序列在时间上平移时长T后形成，如式（4）所示。当选取合适的平移时长T时，可使得两模拟风速序列的相关系数同实际值相同。

如果平移时长T不是整数，令T=[T]+Δt（[T]不大于T的整数），那么可以通过线性插值的方法，得到 yt的时间序列:

通过以上的方法，可以生成同时满足时序自相关性和互相关性的风速序列和。

2.2 风机出力模型

风电机组完成了将风能转化为电能的过程。风电机组发电功率同风电机组装机容量以及风电机组各项参数密切相关［11］。单台风电机组的发电功率可表示为

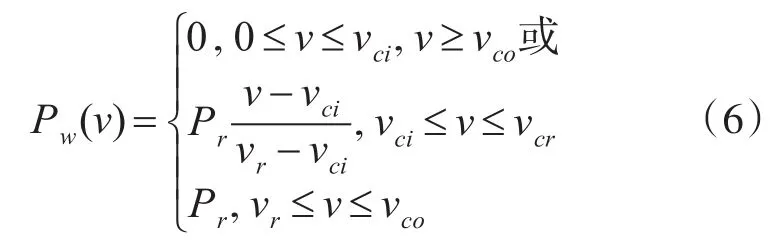
3 含风电发电系统灵活性评估模型

3.1 灵活性资源及需求模型

传统的发电系统调度时考虑需要有一定容量的备用，但未考虑在较短时间尺度下备用容量能否应对可再生能源接入后的净负荷波动情况。所以针对在一定时间尺度下发电系统应对负荷波动的能力及电力系统灵活性，发电系统内各设备向上和向下灵活性资源量化计算公式如下:

1）发电机向上灵活性指标及约束分别为［12］

2）发电机向下灵活性指标及约束分别为［13］

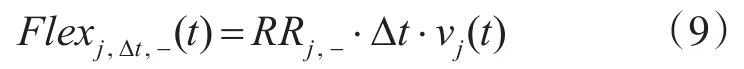
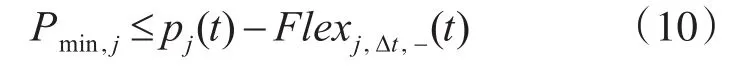
其中，Δt表示相应的时间尺度，RRj,+和RRj,-表示第 j台机组向上和向下爬坡功率，vj(t)表示t时段内第 j台机组是否在线的0-1变量，在线为1，离线则为0，pj(t)为t时刻第 j台发电机组出力，Pmax,j和Pmin,j分别表示第 j台机组最大和最小技术出力。

在确定各抽样时刻时各台发电机组可调度容量即各台发电机组灵活资源后，即可对各时刻各台机组可调度容量进行累加，即得到发电系统灵活性资源指标:

灵活性需求则是研究相应时间区间Δt内不可调度的净负荷的变化量，公式如下:

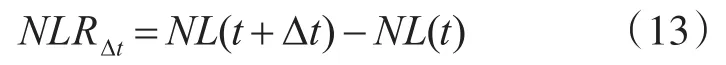
其中，NL(t+Δt)和 NL(t)分别为t+Δt和t时刻的系统净负荷（负荷和风电的差值），NLRΔt定义为系统在Δt时间尺度下t时刻的灵活性需求。

灵活性需求同样具有方向，分为向上和向下灵活性需求:

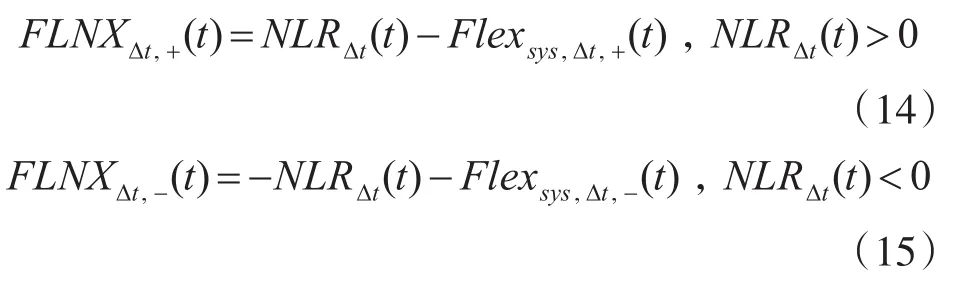
其中，FlexΔt,+(t)和 FlexΔt,-(t)代表系统在 Δt时间尺度下t时刻的向上和向下灵活性不足差额。

3.2 灵活性指标计算

通过计算系统灵活性不足评价指标可以对发电系统灵活性进行量化分析。针对含风电接入的发电系统出力协调能力，本文提出了一系列灵活性评价指标，现对该系列指标作进一步说明:

1）向上灵活性不足概率PLUF:即系统常规机组能够提供的向上灵活性资源不满足系发电统所需向上灵活性需求的概率，求解公式如下:

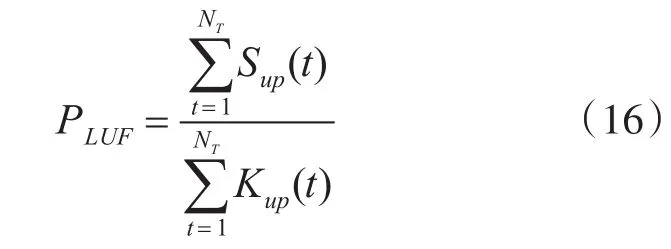
其中，Nt为模拟时间内总的抽样次数，Sup(t)和Kup(t)为0-1变量，前者为1时表示抽样时刻系统有着向上灵活性需求并且大于系统能够提供的向上灵活性资源，即发生向上灵活性不足事件，后者为1时表示抽样时刻系统有着向上的灵活性需求。

2）向下灵活性不足概率PLDF:即系统常规机组能够提供的向下灵活性资源不满足发电系统所需向下灵活性需求的概率，求解公式如下:

其中，Sdown(t)和Kdown(t)为0-1变量，前者为1时表示抽样时刻系统有着向下灵活性需求并且大于系统能够提供的向下灵活性资源，即发生向下灵活性不足事件，后者为1时表示抽样时刻系统有着向下的灵活性需求。

3）向上灵活性不足期望ELUF:即系统常规机组能够提供的向上灵活性资源与系统所需向上灵活性需求差额的期望值，求解公式如下:

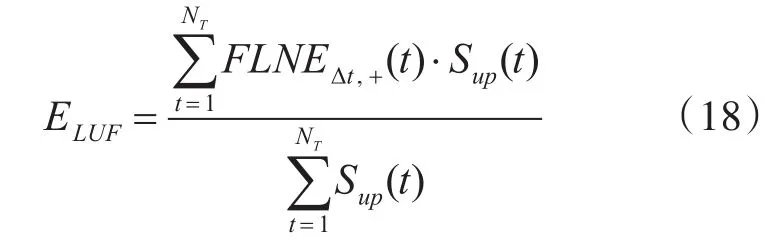
其中，FLNEΔt,+(t)为各时刻系统向上灵活性不足差额。

4）向下灵活性不足期望ELDF:即常规机组能够提供的向下灵活性资源与系统所需向下灵活性需求差额的期望值，求解公式如下:

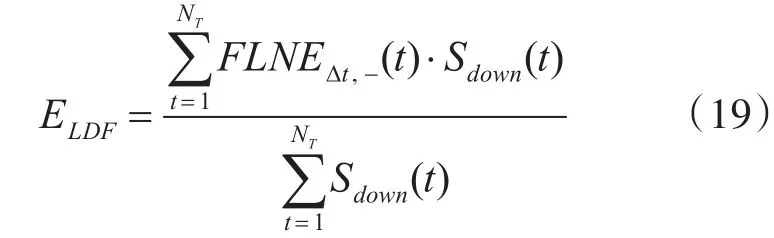
其中，FLNEΔt,-(t)为各时刻系统向下灵活性不足差额。

4 含风电发电系统灵活性评估流程

本文基于序贯蒙特卡洛法［14］，针对上节所提到的灵活性指标的求解给出了相应的流程如下。

步骤1:根据两地风速历史数据，得到两地风速的ARMA模型，并且计及相关性，使用相同的白噪声序列来生成两地风速序列Vx,t和Vy,t，对Vx,t不做处理，使用二分法［15］将Vy,t平移时间T得到序列，使得Vx,t和Vy*,t的相关性与两地历史风速相关性一致，得到风速序列；

步骤2:根据风速数据、负荷数据、机组相关参数、常规发电机组相关约束等相关数据，通过最优调度的目标函数，求解确定该日各小时各台常规机组出力状态；

步骤3:在确定调度日每小时各机组出力状态后，求解发电系统各时刻的可调度容量，即各时刻相应时间尺度下的灵活性资源 Flexsys,Δt,+(t)和Flexsys,Δt,-(t)情况，针对各抽样时刻点依次计算系统在相应时间尺度Δt下的灵活性需求NLRΔt,+(t)、NLRΔt,-(t)情况；

步骤4:根据灵活性需求方向，比较灵活性需求和灵活性资源的大小，计算相应灵活性不足次数、灵活性不足量 FLNEΔt,+(t)和 FLNEΔt,-(t)等灵活性参数，并求解PLDP、PLDF、ELUF和ELDF等各项灵活性指标；

步骤5:比较各项灵活性指标收敛与否，若收敛则得到各项灵活性指标；若未收敛，则返回流程步骤1，进入下一调度日计算。

5 算例分析

5.1 参数设置

本文对某系统进行灵活性评估，系统共含10台风电机组，总装机容量1662MW，系统峰值负荷为1500MW，每小时负荷数据采用IEEE-RTS79标准测试系统中全年负荷数据，常规机组爬坡率取装机容量的60%。风机的切入风速、额定风速、切出风速为4m/s，15m/s，25m/s。对该算例进行灵活性评估时，首先要进行日前经济调度，调度周期为24h，调度精度为1h，削负荷惩罚费用为4000元/MWh，弃风惩罚费用为400元/MWh。本文算例中求解精度为各项灵活性指标方差均收敛至0.05以内。

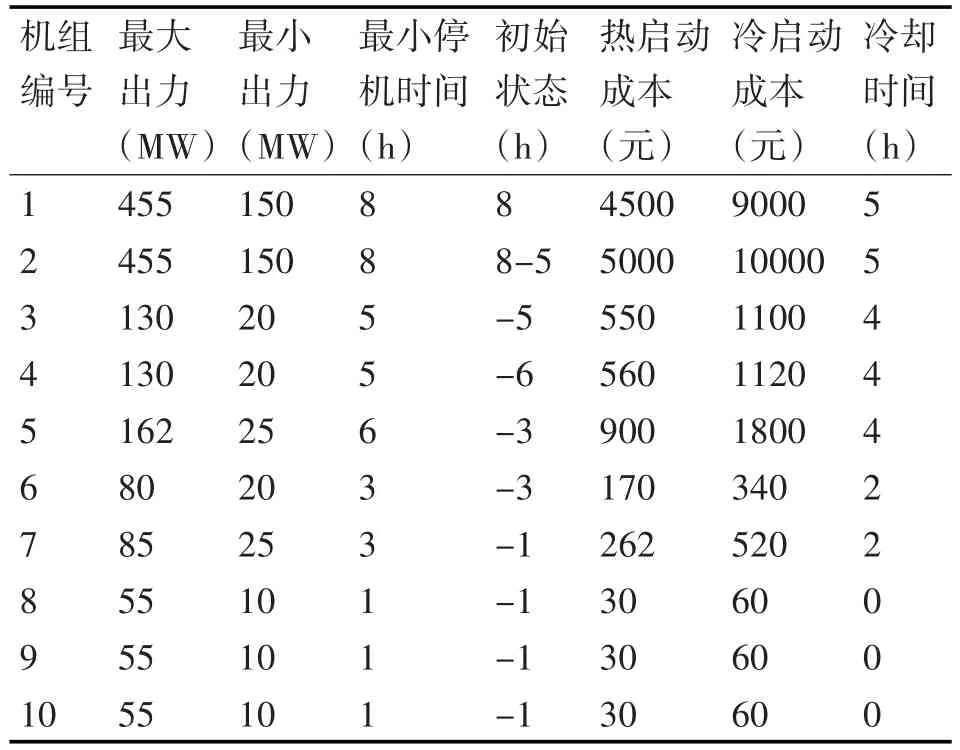
表1 常规机组相关参数

5.2 相关性风速生成

选择贵州电网有限责任公司数据库中所收录的惠水县和龙里县两个地区10年的风速数据（2008年-2017年）来验证ARMA风速时移方法所生成相关性风速的可行性和有效性。惠水县和龙里县两地区之间直线距离约为56km，历史风速序列的相关统计参数如表2所示。

表2 两地区历史风速相关统计参数

得到两地风速序列的ARMA(3,2)模型如下:惠水县地区:

龙里县地区:

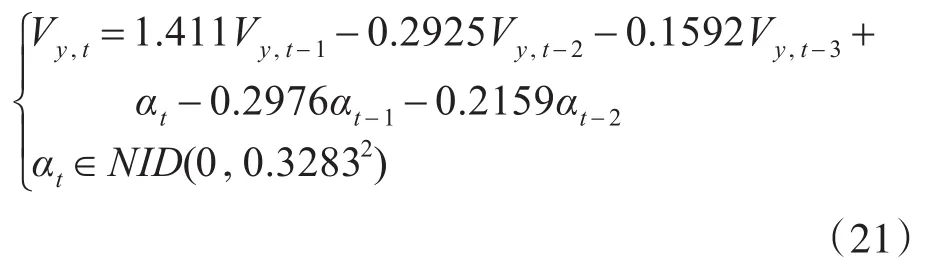
其中，NID表示正态且独立分布，而对于两风电场的模拟风速序列，首先确定两地ARMA风速模型，其次生成惠水县地区50年的模拟风速序列Vx,t，利用该模拟风速序列以及最优平移时长的确定方法，计算得到最优平移时长T以及具有相关性的50年龙里县地区的模拟风速序列Vy*,t，并且计算两组风速序列相关统计参数，如表3所示。

表3 两地区模拟风速相关统计参数

计算得到满足两地区实际风速相关性的平移时长为2.4h，通过对比表3和表2中的数据可以看出，时移ARMA模型能够较好地保有原有历史风速数据的相关统计参数，尤其是保有了历史风速序列之间的相关性，模拟数据与历史数据各统计参数较为接近，可以认为模拟风速数据具有了相同的统计特性。

图1展现了不同相关性的情况下，惠水县和龙里县地区不同的模拟时序风速，当两模拟时序风速相关系数被设定为0.8351时，可以看出两地区风速之间高度相关，两模拟时序风速在同一时刻变化趋势大多相近；当两模拟时序风速的相关系数被设定为0.1时，可以看出两地区风速之间关系近乎为独立，两模拟时序风速在同一时刻变化趋势相差较大。

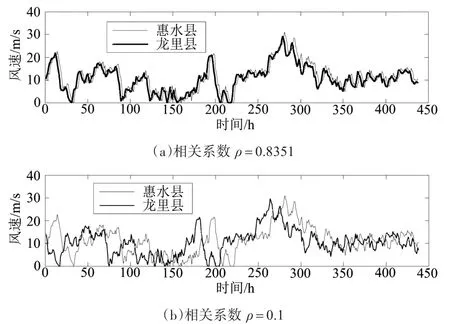
图1 不同相关性情况下两地区模拟时序风速

5.3 风速相关性对灵活性的影响

Case1:不考虑两风电场风速相关性，即两风电场风速无相关性；

Case2:考虑两风电场风速相关性，且相关系数为历史风速实际值；

Case3:考虑两风电场风速相关性，且高度相关。

使用时移方法生成相关风速，对发电系统进行灵活性评估，为体现相关性对灵活性的影响，分别设定Case1-3风速相关系数为0.1、0.8351（实际相关系数）和0.9961（时移为0h时最高相关性），计算得到的灵活性指标如表4所示。

表4 不同相关系数下系统灵活性指标

从表4中可以看出，无论是否考虑常规机组故障，算例的三种情况中，系统灵活性指标均有一定的差异，在不计风速相关性的情况下，系统的灵活性指标最低，意味着系统灵活性水平更好，这表明两风电场风速之间如果存在着过高的相关性，将会对系统的灵活性产生不利的影响，如果无视相关性将会导致对发电系统灵活性的评估结果过于乐观。

图2和图3给出了采用序贯蒙特卡洛法得到的系统各灵活性指标与两风电场风速相关性之间的关系曲线。从图中也可以看出，随着风速之间相关性的降低，系统各灵活性指标均呈下降趋势，这表明对于多风电接入的发电系统，多风电场风速之间的独立性可以对系统灵活性产生积极影响，所以在对接入同一系统的风电场位置进行布局时，分布在风速相对独立的位置可以有效降低由于风速波动性对系统灵活性所造成的影响。同时也可以看出，随着风速相关系数的降低，系统灵活性指标降低速度变慢，尤其是对向下灵活性指标而言趋势更为明显。

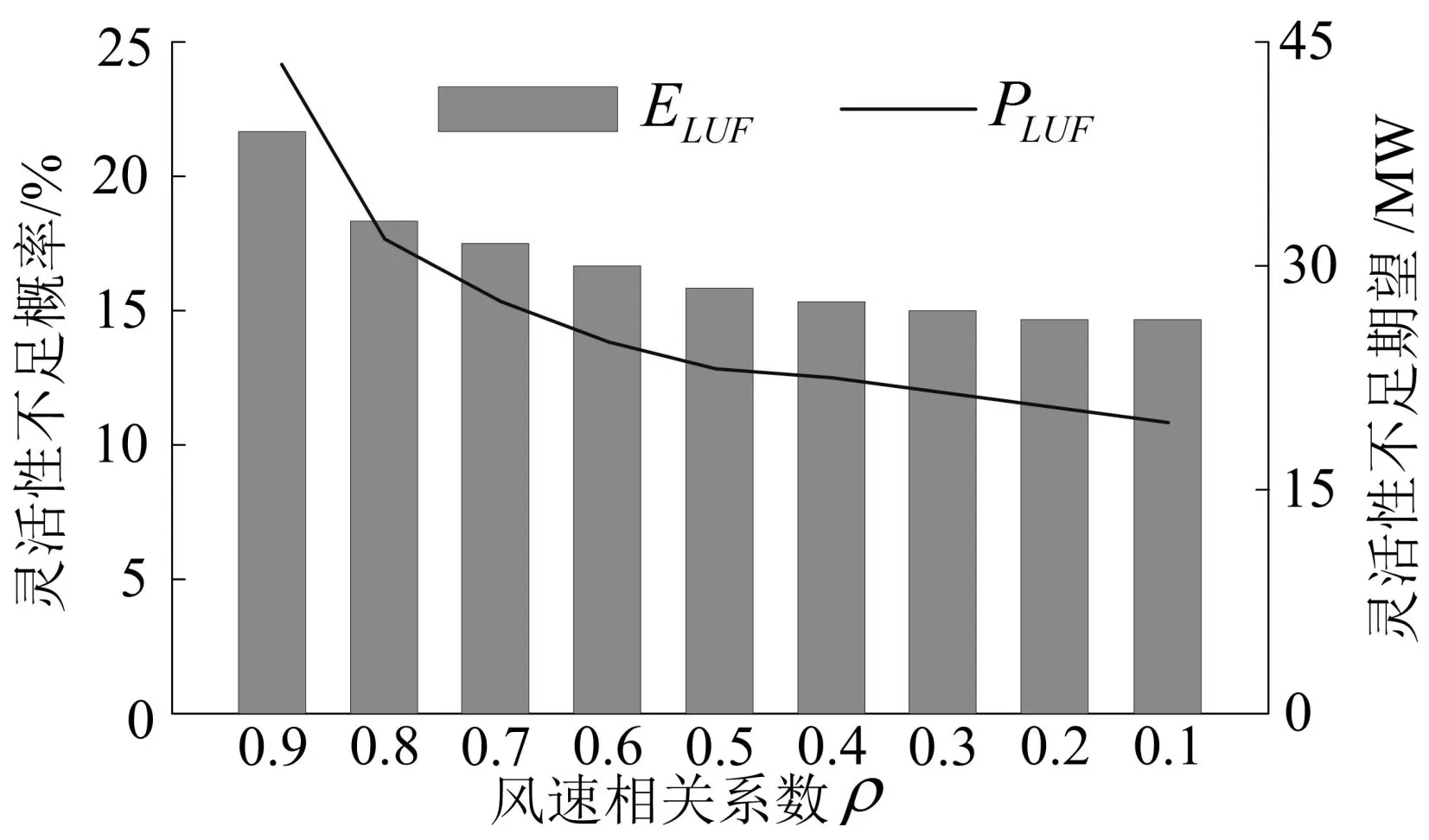
图2 向上灵活性指标同风速相关性关系

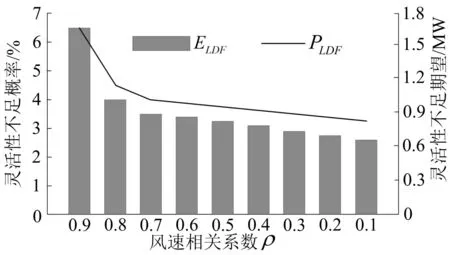
图3 向下灵活性指标同风速相关性关系

5.4 多风电场容量配比对灵活性的影响

当同时有多个风电场接入同一发电系统时，在接入总容量一定的情况下，两风电场之间容量的大小也会在一定程度上对发电系统灵活性造成一定的影响，本文考虑两风电场风速在实际相关性的情况下，依次修改两风电场的接入容量，研究发电系统灵活性指标同接入容量比例之间的关系。

将两风电场接入比例以10%为间隔变化，由0%:100%逐渐变为100%:0%，各灵活性指标变化如图4和图5所示。

图4 向上灵活性指标同两风电场容量配比之间关系

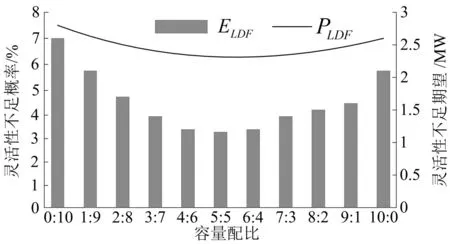
图5 向下灵活性指标同两风电场容量配比之间关系

由图4和图5可知，随着两风电场接入容量比例的变化，发电系统向上灵活性和向下灵活性各项指标均出现先下降再上升的过程，即系统灵活性水平先变得较优而后变得较差。尤其是当两风电场接入容量比例接近50%:50%时，系统灵活性指标达到了最优。由此可以看出，在风况相近的两个地区，在进行风电场容量规划的时候，应实际考虑容量配比给系统灵活性带来的影响，合理均衡规划两风电场容量，从而尽可能降低风电接入对系统灵活性的影响。

6 结语

地理位置上相近的地区的风电场之间的风速的相关统计参数较为相近，不同风电场的风速在同一时刻有着相近的变化趋势，在数据统计上体现出了一定的相关性，这种相关性在电力系统灵活性评估中有着一定的影响。本文采用时移ARMA模型，利用二分法计算最优平移时长，产生同时考虑自相关性互相关性的模拟风速序列，并且利用符合实际相关性的风速，对多风电场接入的发电系统灵活性进行评估，并且研究相关因素对灵活性的影响。

通过算例分析部分，得到以下结论:1）随着两风电场风速相关系数的降低，发电系统的灵活性指标降低，系统灵活性水平变得更好，因为相关性较低的情况下，两者风速之间会有一定的互补，使得总体风速功率输出更为平稳，系统灵活性需求降低，系统灵活性变好；2）当位置相近的两风电场接入同一发电系统时，需考虑两者容量配比对系统灵活性的影响。通常情况下两风电场容量均匀配置可以降低系统灵活性指标，提高系统灵活性水平。