基于快速迭代插值的FMCW 雷达距离估计算法

段永昌，李欣，黄耀辉，黄平

（1.中国舰船研究设计中心，湖北 武汉 430064；2.哈尔滨工程大学工程训练中心，黑龙江 哈尔滨 150001；3.哈尔滨工程大学自动化学院，黑龙江 哈尔滨 150001）

1 引言

调频连续波（FMCW,frequency modulated continuous wave）雷达具有良好的测速测距性能，被广泛应用于无人驾驶[1]、医疗监护[2]、信道估计[3]等方面。然而，传统FMCW 雷达存在栅栏效应和频谱泄露的问题，导致距离的估计偏差较大。为了更准确地估计目标距离，目前常用的方法有采样序列直接补零法、基于复调制的ZFFT（zoom-fast Fourier transform）方法、FFT-DTFT（FFT-discretetime Fourier transform）、Chirp-Z 变换[4]。但以上4种方法存在计算量大、估计误差大等缺点。文献[5]将拟合法加入传统的ZFFT 算法中，提高了频率估计精度，降低了计算量，但该算法的滤波器阶数高，实现难度较大。文献[6]对基带信号进行空间变换，并对变换后的信号进行均匀插值，从而获取更精确的频率值，但该方法本质上仍然是FFT-DTFT 方法，精确度受均匀插值点精度的限制。

近些年，一些基于最大似然估计的频率估计方法被提出[7-10]，这些方法同样可用于距离估计。文献[7]提出了一种单频信号下的迭代插值算法，利用插值结果在迭代的过程中逐步修正偏差。文献[8]提出了一种基于DFT（direct Fourier transform）样本的频率偏差校正方法，该算法不需要迭代，直接利用与目标相关的3 个DFT 样本对偏差进行估计。在文献[8]的基础上，文献[9]增加了偏差校正因子，提高了精度，但文献[8-9]存在估计误差不均匀的问题。文献[10]提出了利用细化频谱对信号进行插值的方法，解决了估计误差不均匀的问题。文献[7-10]提出的方法对单频信号的偏差估计具有良好的效果，但是应用在多目标环境时，频谱间干扰会造成距离估计的偏差增大。为了解决此问题，文献[11]提出了基于高阶多项式插值补偿估计偏差的方法，其利用高阶多项式拟合出信号的频谱，获得每个目标的精确频率值，但该算法计算量大，不利于硬件实现。文献[12]在文献[11]的基础上提出了加窗抑制频谱干扰的方法，利用窗函数抑制旁瓣的干扰。文献[11-12]所提方法存在频谱展宽影响估计性能的问题。在 DoA（direction of arrival）估计领域中，文献[13-14]提出利用迭代逐步校正角度偏差的方法，可以避免频谱展宽的问题，同时还可以解决多目标角度之间的干扰。但该方法应用在FMCW 雷达系统存在以下问题：在粗估的过程中需要把目标个数作为先验信息，且对每个目标谱峰估计时都需要对原始数据修正，增加了算法的复杂度。

受迭代校正思想解决多目标情况下频谱干扰的启发，本文提出一种改进的基于快速迭代插值的FMCW雷达距离估计算法，通过恒虚警检测的方法粗估出目标的位置，解决不同距离的目标个数作为先验信息的问题，迭代过程中利用修正偏差因子替代对原始数据重复修正的过程，简化了处理过程，更利于硬件实现。理论仿真和实测数据验证了算法的可行性。

2 FMCW 信号模型

本文采用的FMCW 雷达系统结构如图1 所示，包括发射信号单元、接收信号单元、混频器、低通滤波器、A/D 模块、信号处理芯片及FMCW 信号发生器。整个系统的工作机制描述如下，波形信号发生器产生发射信号包络，经过压腔振荡器调制之后的锯齿波信号由发射天线发射，再经过目标反射之后由接收天线接收，发射信号与接收信号进行混频，经低通滤波器滤波后得到中频信号，经过A/D 转换后送入信号处理芯片进行处理，得到目标的估计速度和估计距离[15]。

图1 FMCW 雷达系统结构

FMCW 雷达系统的发射信号模型[16]可表示为

其中，R0是目标在t=0 时刻的距离，v是目标的运动速度，c 表示光速。在忽略噪声的情况下,接收信号模型可表示为

其中，时间t∈(td,T+td)；Kr表示与目标反射强度及信号传播衰减相关的常数；sT(t)与sR(t)在时间域进行混频，并通过低通滤波器滤去镜像分量即可得到中频信号，如式(4)所示。

其中，指数项可以分为3 个部分，第一部分为距离时延和速度多普勒引起的混合频率，第二部分和第三部分都是距离时延引起的相位变化，第三部分的相位变化远小于第二项，可以忽略。在测量近距离低速目标时，Ktd远大于fd，也可以忽略。由此得到中频信号的近似模型如式(5)所示。

此时，式(5)与估计静态目标距离的中频信号模型一致，在估计运动目标速度时，可以发射多个调频脉冲并采样，得到的中频信号如式(6)所示。

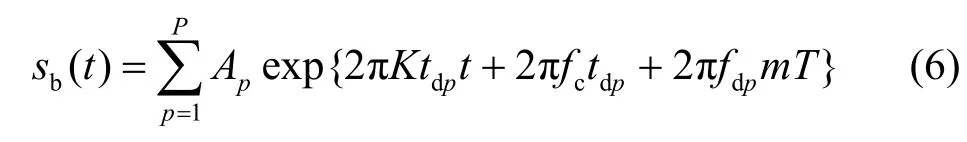
其中，tdp和fdp表示第p个目标的时延和速度引起的多普勒频率；P表示目标的个数且P≥1，n=0,1,…,N，N表示 A/D 采样的数据长度；m=0,1,…,M，M表示发射的脉冲数；Ap表示第p个目标的信号幅值。于是，通过对单个脉冲的快采样进行傅里叶变换即可获得目标的距离对应的频率，对多个脉冲的慢采样进行傅里叶变换即可获得目标的速度对应的多普勒频率。这样对一串调频连续波脉冲进行2 次傅里叶变换就可以得到目标的距离和速度估计值。

3 基于迭代插值的距离估计算法

本文提出的算法由粗估和精估两部分组成。通过FFT实现对不同距离不同方向的目标的个数P及第p个目标所在的距离单元mp的估计。精估的过程包括Q次迭代，在每次迭代过程中通过频谱泄露减法策略去除其余p-1 个频谱对当前频谱的干扰，利用去除掉干扰的频谱得到偏差的估计值，通过多次迭代，使更接近真实的偏差δ。

第p个目标的频率为

其中，fs表示信号的采样频率；δ是FFT 栅栏效应引起的偏差，且δ∈[-0.5,0.5]。通过对中频信号sb(t)进行FFT[17]及CFAR 算法[18]估计出目标所在的距离单元mi=1,2,…,P，其中，P表示不同距离的目标个数。对中频信号进行单个脉冲内的快采样FFT 如式(7)所示。

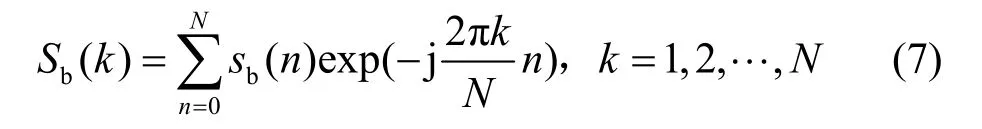
其中，sb(n)表示经过A/D 采样之后的中频信号，N表示FFT 的点数，Sb(k)表示频域内第k个单元的值。对Sb(k)进行CFAR 处理估计出背景噪声的功率水平，然后将Sb(k)与背景噪声功率水平进行比较，估计出不同距离的目标个数P，如式(8)所示。

其中，CFAR(Sb(k))表示对Sb(k)做恒虚警检测的结果，即背景噪声功率；Count 表示对Sb(k)＞CFAR(Sb(k))的单元个数进行统计，统计的结果即为不同距离的目标个数。另外，还需对恒虚警检测后的结果进行聚心处理，即忽略目标附近的低幅值谱峰，避免因频谱泄露而将噪声误认作目标，导致虚警率上升。完成目标检测后提取目标所在的频谱单元，并作为估计频谱单元偏差基础。第P个目标所在的频谱单元mp如式(9)所示。

真实的频率值表达式由两部分组成：整数网格点和待估计偏差，因此当估计的偏差逼近真实的频率偏差mδ时即可得到精确的频率信息，从而得到真实的距离信息。考虑到多目标条件下目标信号之间的干扰，需要利用迭代的思想不断将频谱间的干扰去除，从而将多目标距离估计的问题转化为单目标距离估计的问题。

为了便于描述，令Si=Sb(mi)，Sb(mi)表示频域内第mi个频谱单元的谱峰，则第个单元的谱峰可表示为。

以第p个目标为例，说明进行FFT 之后的频谱成分。假设频率偏差估计量为，直接利用中频信号在处进行FFT，得到的频谱峰包含以下三部分：第p个目标反射信号进行FFT 的幅值、其他目标反射信号在处的泄露、噪声对幅值的干扰。其中，噪声干扰对谱峰的影响相对于频谱间的干扰较小，可忽略。第l个目标在第mp+个频谱单元的泄露可通过该目标反射信号在第mp+个频谱单元进行FFT 得到，如式(10)所示。

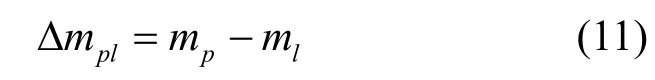
Δδpl表示第p个目标对应的频谱单元偏差与第l个目标对应的频谱单元偏差在频域内的距离，如式(12)所示。

由此可得第p个目标的反射信号强度如式(13)所示。

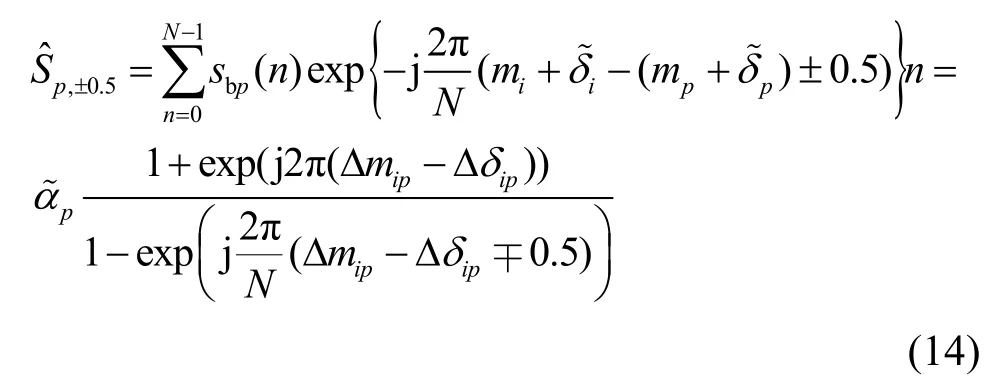
其中，Δmip表示第i个目标对应的频谱单元mi与第p个目标对应的频谱单元的mp在频域内的距离，如式(15)所示。

Δδip表示第i个目标对应的频谱单元偏差与第p个目标对应的频谱单元偏差在频域内的距离，如式(16)所示。

对中频信号直接进行FFT 可得到谱峰Si,±0.5，Si,±0.5由两部分组成：第i个目标反射信号在第个频谱单元进行FFT 得到的谱峰及第p个目标反射信号在第个频谱单元的增强，由此可知的表达式为

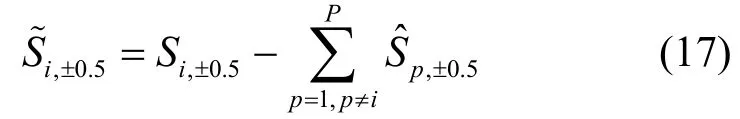
其中，i=1,…,P，fs是A/D 采样频率，c 是光速，B是调频带宽，T表示锯齿波的周期。

本文提出的基于快速迭代插值的FMCW 雷达距离估计算法包括以下步骤。

步骤1对A/D 采样之后的中频信号进行FFT，然后利用CFAR 算法估计出目标个数P及目标所在的频谱单元mi，i=1,2,…,P。

步骤2计算第i个目标的频谱单元mi对应的频谱单元偏差，i=1,2,…,P。

步骤2.1设定目标迭代次数Q，并令当前迭代次数q=0，对单次迭代之后第i个目标的偏差估计值及幅值估计量进行初始化，令=0，i=1,2,…,P；

步骤2.2估计第p个目标的反射信号强度，p=1,2,…,P；

步骤2.3利用计算第p个目标对第i个目标产生的频谱干扰；

步骤2.4计算去除干扰后第个频谱单元的谱峰；

步骤2.5利用谱峰计算偏差校正因子和频谱单元偏差；

步骤2.6q←q+1，若q≤Q，则重复步骤2.2～步骤2.5。

步骤3利用频谱单元im及频谱单元偏差计算第i个目标反射信号的频率fi及目标的距离值Ri。

4 仿真及硬件验证

为验证算法的性能，本文选择以下3 种典型的方法进行对比：改进的Zoom-FFT 算法[5]、基于非迭代的 Candan 算法[9]、加窗抑制频率泄露的Hamming-window 算法[12]。仿真参数设置如表1 所示。性能的衡量指标用距离均方根误差（RMSE,root mean squared error）描述，定义如下。

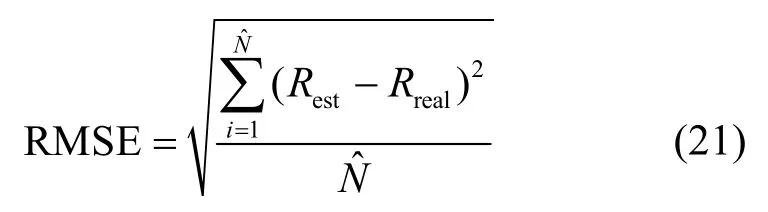
其中，Rest表示距离的估计值，Rreal表示距离的真实值，表示蒙特卡罗实验次数，本文中取=2 000。

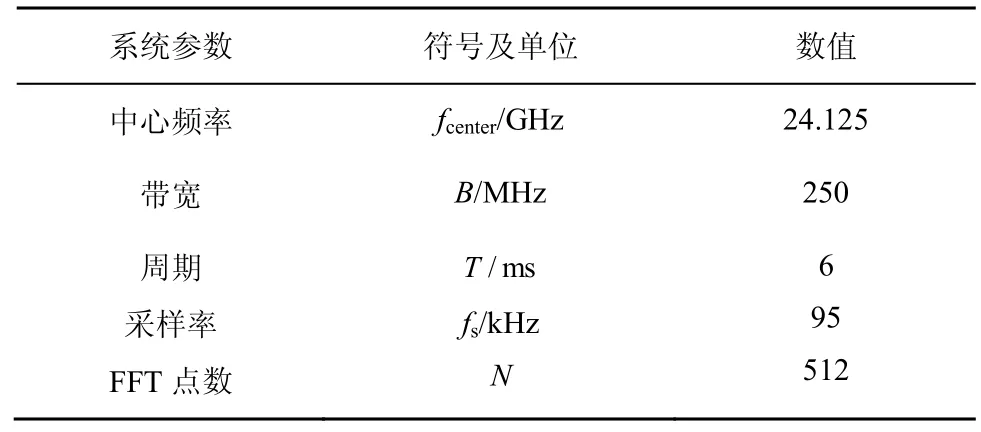
表1 系统及仿真参数

4.1 回波信号强度对算法的影响

本节验证信号强度不同对算法精度的影响，2个目标的信号幅值满足A2=0.5A1。图2 和图3 是本文算法与3 种对比算法输出的RMSE 随着信噪比（SNR,signal to noise ratio）的变化曲线。

图2 目标1 在不同SNR 下的RMSE

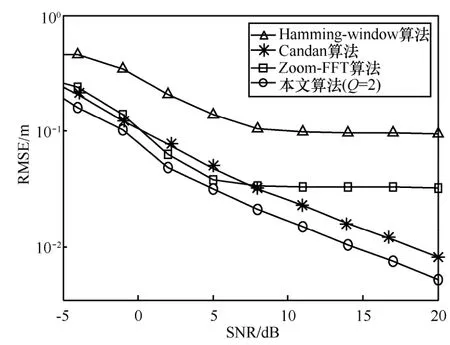
图3 目标2 在不同SNR 下的RMSE

从图2 可看出，相比于其他3 种算法，本文算法在同样的SNR 下具有更好的估计性能。此外，Zoom-FFT 算法RMSE 曲线趋于平坦，这是因为该算法的估计精度受局部细化倍数的限制，导致距离的偏差值不随SNR 变化。

从图3 可看出，本文算法及Candan 算法对目标2 的偏差估计也具有较好的性能。这是因为，2种算法都是通过目标临近的谱峰对偏差估计，受目标1 干扰引起的峰值的变化几乎相同，因此，不会影响2 种算法的估计性能。另外，Hamming-window算法在目标1 的干扰下影响了偏差校正因子的估计，导致距离估计失败。

4.2 采样点数对算法的影响

图4是目标2的信号采样点数对RMSE的影响。2 个目标的信号幅值满足A2=0.5A1，且SNR=15 dB。通过实验 1 可知，Hamming-window 算法和Zoom-FFT 算法在该条件下对偏差估计误差较大，因此选择Candan 算法作对比。目标1 和目标2 的仿真结果相同，因此只给出了目标2 的仿真结果。从图4 中可以看出，与Candan 算法相比，本文算法在迭代次数Q较少时就可获得较小的RMSE，且在相同的采样点数下RMSE 更小。

图4 目标2 采样点数N对RMSE 的影响

4.3 多目标同时探测时的仿真表现

分析算法在多目标下的仿真估计性能，表2 是10个目标下的仿真结果，目标的信号强度变化范围为A∈[0.3,1]，其中，A=1 表示目标反射时无信号损失；最后一列的频率值是整数网格点和待估计偏差之和。从表2 中可看出，信号幅值对本文提出的非均匀迭代插值算法在距离估计中影响很小，另外从表2 中可看出，目标6、7、8 之间的距离差距不足0.5 m，算法对每个目标的估计误差都很小，这是因为算法在迭代的过程中抑制了频谱干扰对偏差估计的影响。

表2 多目标的仿真参数及结果

图5 是不同算法对表2 中目标进行仿真的RMSE。从图5 中可看出，本文算法估计误差稳定在0.1 m 以下，相比于其他2 种算法，估计误差更均匀，RMSE 更小。结合表2 中信号强度发现本文算法估计偏差受到信号强度的影响较小，这是因为，信号的干扰引起的频谱的变化均可以通过本文算法抑制掉，利用无干扰的频谱估计出的距离误差更小。从图5 中还可看出，Zoom-FFT算法估计误差表现为随机性误差，这是由均匀插值导致的。

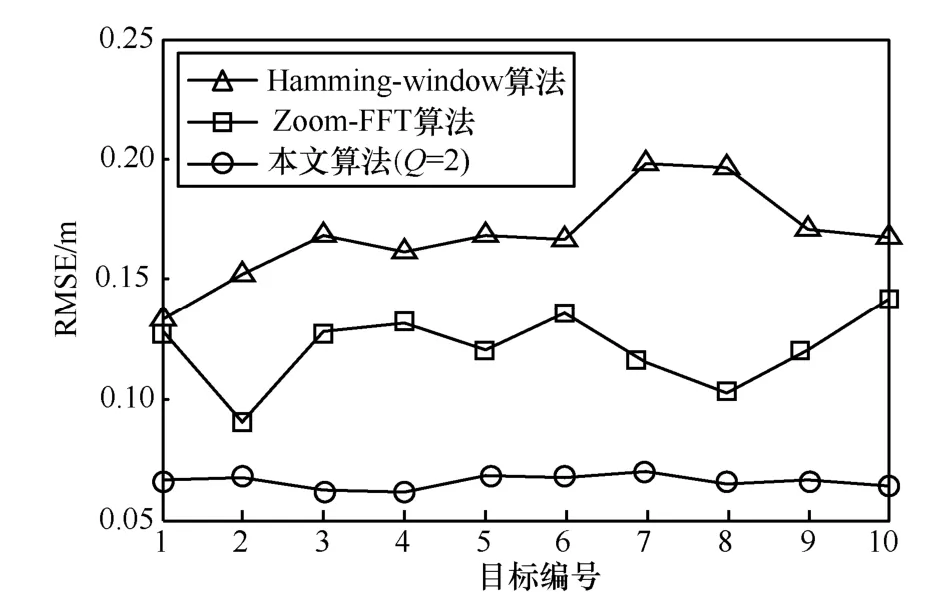
图5 多目标下不同算法的RMSE

图6 和图7 是本文算法与Zoom-FFT 算法对目标3、目标8 局部进行放大的结果。从图6 和图7中可知，通过改变迭代次数Q可以提高精确度，与Zoom-FFT 算法相比，本文算法更接近真实频率，精确度更高。

图6 目标3 局部细化的结果

4.4 不同算法的复杂度比较

表3 是不同算法的复杂度及Matlab 仿真时间，对于本文算法和Zoom-FFT 算法，它们的复杂度主要与迭代次数、插值系数及FFT 运算次数的有关，Hamming-window 算法的复杂度主要与数据加窗、FFT 运算次数有关。仿真目标个数P=10，迭代次数Q=2，Zoom-FFT 算法的插值倍数D=10。从表3 中可知，本文算法的复杂度略低于另外2 种算法。

图7 目标8 局部细化的结果

4.5 静止多目标探测测试

比较3 种算法在实际环境下的近距离多目标距离估计性能。图8 是实际环境测试图与使用的FMCW 雷达硬件系统，表4～表6 分别是Zoom-FFT算法、Hamming-window 算法和本文算法在近距离下对6 个相同的静止目标的探测结果。通过比较表4～表6 可以发现，使用Zoom-FFT 算法的结果与真实值有较大偏差，而Hamming-window 算法和本文算法在近距离探测时可以较好地估计目标的距离，两者的性能也很接近。

图8 实际环境测试图和FMCW 雷达系统

表4 使用Zoom-FFT 算法探测多目标结果

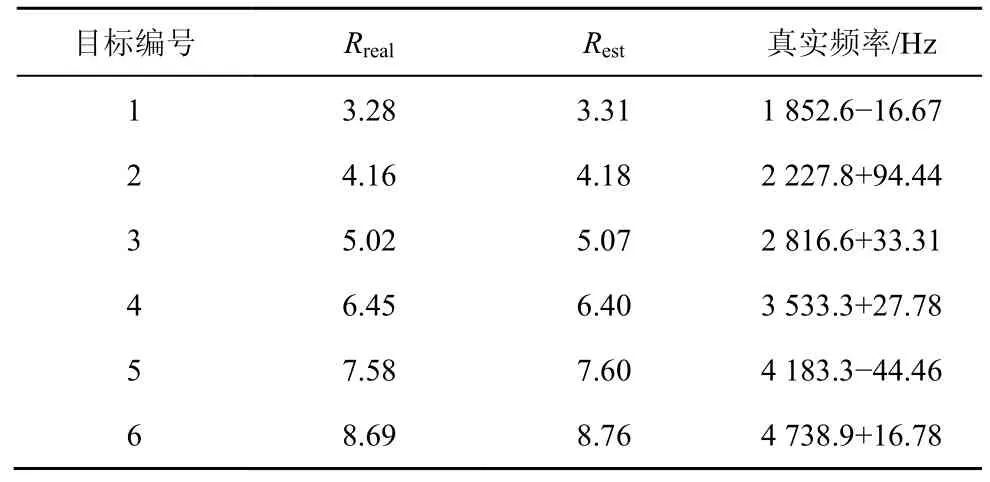
表5 使用Hamming-window 算法探测多目标结果

表6 使用本文算法探测多目标结果

4.6 运动目标探测测试

使用FMCW 雷达对均速直线行驶的汽车进行探测，目标以2.6 m/s 的速度匀速驶近雷达，取目标在运动过程中的一段位移，其探测结果和距离误差如图9 和图10 所示。可以看出，FMCW 雷达在使用4 种算法时都能较为准确地探测近距离的低速运动目标并画出其运动曲线图。

4.7 不同距离目标探测测试

在实际环境测试实验中，目标1 保持静止在14.6 m 处；目标2 在8～10 m 范围内，每隔0.2 m移动一次。FMCW 雷达对2 个目标探测的测试结果及目标的真实值如图11 所示。

从4.4 节～4.7 节的实验可看出，使用非均匀迭代插值算法后FMCW 雷达输出的结果非常接近目标的真实距离，且误差基本保持在20 cm 以内。此外，FMCW 雷达数据每秒可更新多次，该算法完全达到实时性的要求。

图9 运动目标的距离速度曲线

图10 4 种算法的距离误差曲线

图11 双目标真实距离与FMCW 雷达输出结果

5 结束语

针对多目标环境中出现的频谱干扰导致距离估计精度下降的问题，本文改进了一种迭代插值去除频谱间干扰的算法，并将该算法与文献[5,9,12]对比，证明该算法具有良好的抗噪性能且多目标环境中距离估计误差更小，计算复杂度更低。最后，通过硬件实现，证明该算法可在工程中应用。