基于节点通信行为时序的指控信息流挖掘算法

项英倬，徐正国，游凌

（盲信号处理国家重点实验室，四川 成都 610041）

1 引言

通信网络中的指控信息流是指一条指控信息在网络中传播所经过的一条有向路径，比如节点A将一个条指控传给了节点B，命令B 去通知节点C某个事情，那么可以认为一条指令由A 发出，经过B 到达了C，A—B—C 构成了一条指控信息流。通信网络中指控信息流在僵尸网络发现、入侵检测，甚至是对网络中节点之间关系的挖掘都具有重要的意义。一般来说，指控信息流的挖掘方法大多依赖于双方通信的内容。比如，在僵尸网络的挖掘中，文献[1-2]通过提取数据内容和属性的指控特征，动态分析系统执行恶意样本所产生的流量，发现僵尸网络或恶意软件中的指控信息流。文献[3-5]给出了多组通信数据的统计特征，并据此区分网络中的指控信息流和正常的流量。文献[6]使用语义模型来分析通信流量中的负载，并以此对信息流的安全性进行分析。而社交网络中，文献[7-12]通过Hashtags、主题信息、内容信息、转发时延、网络连接等属性，利用机器学习中贝叶斯网络等有监督的方法学习网络中指控信息流的特征。这些方法均假设可以直接观测到通信的全部内容或者部分内容，然而在许多场景中无法获取到通信的内容，仅知道通信发生的时间，例如加密通信数据中指控信息流的挖掘问题。针对这种情况，目前并没有有效的算法，本文将针对通信内容未知情况下的指控信息流挖掘问题进行研究，该问题的难点在于网络中存在着大量的非指控信息流（背景流量），而指控信息流通常淹没在其中，难以挖掘。

2 节点通信行为模型

2.1 问题描述

为了更好地介绍本文研究的问题和模型，下面给出一些概念的定义。

定义1通信网络G(V,E)中的一个指控信息流c指一条指控信息从单一的节点出发，传播所经过的所有节点及有向路径构成的联通子图。

定义2通信网络G(V,E)中，节点vi的行为时序ai指观测到的节点通信行为及发生通信行为的时间t所构成的序列，如式(1)所示。

定义2 给出了通信网络中节点行为时序的定义，本文研究的问题是通过已知的节点行为时序Ac:=[a1,a2,…,an]，推断出通信网络G(V,E)中存在的指控信息流C=[c1,c2,…,ck]。由于通信网络中节点的通信行为未必全都是指控信息，节点之间也会存在着正常通信，在无法得知通信内容的情况下，只能通过节点行为的相关性及网络结构的特性来分析。图1 给出了几个节点的行为时序及由此推测得到的一个指控信息流，其中A～D 代表4 个不同的节点，箭头代表指控信息的传递方向。本文认为，如果节点间通信行为发生的时间比较接近，那么这2 个行为相关的概率就较大，因此转发同一信息（指令）的概率也就越高。

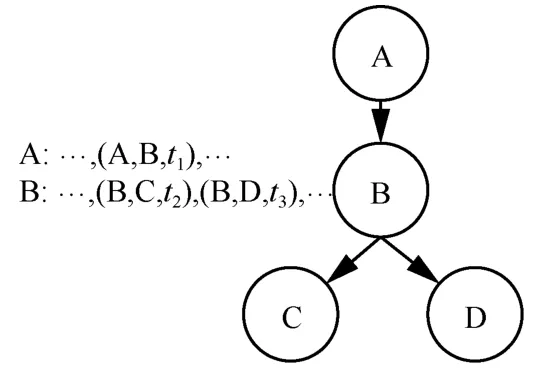
图1 节点行为时序与指控信息流

2.2 通信网络中节点背景通信行为模型

为了对节点的行为进行建模，首先研究节点的背景通信行为。节点的背景通信指节点正常情况下的通信行为，可以认为是除了指控信息通信之外的通信行为。一般情况下，可以假设节点的背景通信行为在时间上有如下特征。

1)节点每次发送信息的行为都是独立的，也就是说节点发送的每条信息前后都没有相关性。

2)节点发送信息的行为在时间上是均匀的。

3)节点的每次通信行为都是单独发生的，2 个通信行为同时发生的概率很低。

4)节点的通信行为在短时间内仅发生一次。

以上假设中的特征在通信网络中是普遍存在的，比如考虑一个节点发送邮件的情况，在不考虑指控信息的情况下回复他人邮件，每次主动发送邮件的行为都是独立的，而且每一封不同邮件的发送方式都是一封一封地发送，这就是假设1)、3)、4)所描述的事情。上述假设2)指在观测的时间内，节点发送一条信息的概率，其与观测时间的长短成正比，可以理解为观测的时间越长，观测到节点发送信息行为的次数越多。而且，这个过程是不依赖于观测的起始时间。例如考虑一个平均每天发送20 封邮件的节点，其5 天内发送邮件的数量大概是其10 天内发送邮件数量的一半。这一点在绝大多数的场景下都可以满足。尽管节点发送信息的时间并不是严格均匀的，比如工作日通信要比周末频繁，但是可以对不同情况分别进行处理。下面将对满足这些条件的通信行为进行建模。

定理1如果一个通信网络中节点的通信行为满足以上4 个假设，那么时间t内节点发送消息的数量N(t)满足齐次泊松过程。

证明该定理的证明参见文献[13-14]中泊松过程的定义和证明。

证毕。

下面，考察通信网络中节点的通信时间间隔分布情况。

定理2在满足以上4 个假设的通信网络中，令Xn表示某一节点第n-1次通信行为和第n次通信行为之间的时间间隔，那么Xn(n=1,2,…)为独立同分布的指数随机变量。

证明由定理1 可知，在时间t内节点发送消息的数量N(t)满足齐次泊松过程。根据文献[13-14]中泊松分布的相关定理可以证明该定理。

证毕。

定理2 表明，在没有指控信息的情况下，节点相邻2 次通信时间间隔的分布满足强度为λ的指数分布，其均值为。然而对于指控信息的转发，其发送行为是被动的，而且通常会在较短的时间内对指控信息做出反应，这样，节点发送指控信息的时间间隔不会满足指数分布。

2.3 通信网络中节点的指控通信行为建模

对于通信网络中的指控信息，假设其具有如下的特征。

1)节点在收到指控信息后会在相对较短的时间内执行该指控信息。

2)节点对指控信息的执行并不影响其正常的通信行为。

该假设容易理解，也符合绝大多数实际情况中节点执行指控信息的情况[15]。从这2 个假设出发，对于通信网络中的指控信息流，节点在收到指控后的行为显然不满足2.2 节中的假设，因为通常收到指控的一方会在较短的时间内做出回应。考虑节点A 命令节点B 发送消息给节点C，这种情况下B 发送消息给C 的行为是由A 发送消息给B 激发的，这一过程必然不是独立的。又如通信中A 与B 进行聊天，双方发送消息的行为显然也不是独立的。由于指控信息流与非指控信息流之间存在的这种差异，给区分这2 种信息提供了可能。文献[15-16]研究表明，节点转发指令的时间间隔服从指数分布或者幂律分布，即

基于指控信息假设的特征2)，考虑到节点收到指控信息后的行为并不影响其背景通信的行为，对于每个节点的通信行为序列，去除指控信息通信行为后，便可以得到其正常的信息通信行为序列，根据定理1，该序列满足齐次泊松过程。节点通信行为的示例如图2 所示，其中B 的通信行为序列中的虚线代表其对A 指控信息的回应，去除掉B 中的虚线后，B 的行为序列基本上是一个泊松过程。因此，判断B的通信行为是否是指控信息的一个有效方法是依据的大小。结合定理2，节点对于指控信息的转发，其发送行为是被动的，而且通常会在较短的时间内对指控信息做出反应，这样，节点发送指控信息的时间间隔将会在很大的概率上不能满足指数分布。这样便可以得到一个区分出指控信息的统计量。

图2 节点通信行为示例

由于实际能够观测到的数据是上述2 种信息模型独立生成数据的并集，如何从融合的数据中根据模型筛选出指控信息流是本文的核心问题。

3 模型求解

定理2 给出了节点在无指控信息流时发送信息的时间间隔满足强度为λ的指数分布，众所周知，λ的极大似然估计为，其中，为通信时间间隔的均值。假设网络中的指控信息与正常通信信息的占比为r，一般情况下，r≪1 。设网络中节点j接收到由节点i发送信息的强度为λi,j，则节点j发送信息的强度，即每个子节点发送信息强度的和。易知，节点j接收来自节点i信息的过程是速率为λi,j的泊松过程；节点j发送消息到节点k的过程是速率为λj,k的泊松过程。考虑节点j收到节点i信息的时刻ti,j，以及最近的一次节点j发送消息到节点k的时刻tj,k,那么有

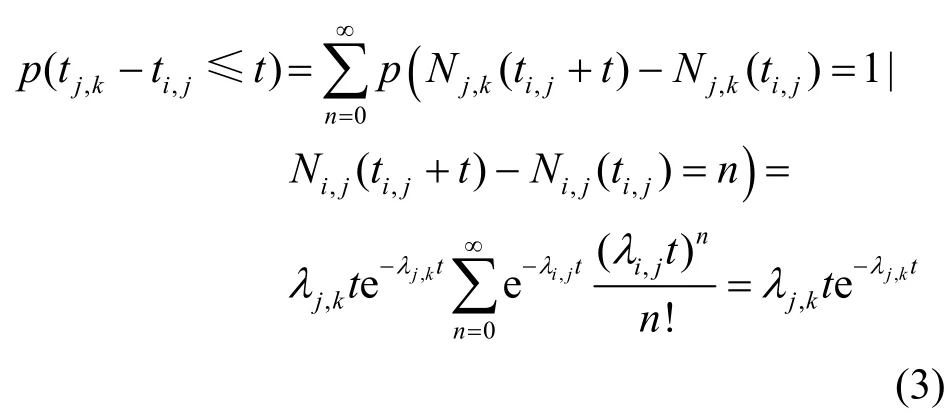
其中，Nj,k(t)指时间t内节点j给节点k发送信息的数量，Ni,j(t)指时间t内节点i给节点j发送信息的数量。从式(3)可以看出，正常通信中，节点收到一条消息后，又恰好在t时间内给特定节点发送一条消息的概率，仅与该节点与特定节点之间发送消息的强度λj,k及t有关，而与接收节点的发送消息强度无关。

对于指控信息的转发，根据2.3 节的分析，其转发时间t的概率为指数分布或者幂律分布。图3给出了3 种分布函数。从图3 中可以看出，节点转发指令的时间间隔概率随着间隔的增加而单调递减，而节点恰好发送正常通信信息的时间间隔概率有一个波峰，其概率先增加后减小。那么，针对如上所述的分布函数，如何选择一个阈值t′才能使分类正确的概率最大。一个直观的答案是选择2 个分布曲线的交点作为阈值，如果小于该阈值，判断为指令转发；如果大于该阈值，判断为正常通信行为。

图3 不同分布函数

基于上述的推理和计算，为了求得阈值，需要首先估计出每个节点发送给相应节点信息的速率λj,k。由于通常情况下指令类信息占比非常少，因此可以采用观测数据中节点通信的频率作为其发送速率的估计值。而转发指令的时间间隔参数α可以采用迭代的方法来估计。算法1 给出了FlowMine算法对网络信息流的挖掘，具体如下。

算法1FlowMine 算法

输入Ac:=[a1,a2,…,an]，信息流最大长度ML，跳出临界值e

算法1 中Δt表示发送相邻信息的时间间隔，|Δt|表示每次循环后阈值变化的绝对值。该算法的一个关键在于对α的估计，其收敛性及收敛速度直接影响到算法的性能。定理3 给出相应的分析。

定理3已知转发指令的时间间隔服从指数分布或者幂律分布，那么根据FlowMine 算法对α的估计是收敛的。

证明考虑2 个分布的差，如式(4)所示。

在本文假设中，由于α≪λ，且fλ(t)的极值在t=λ处，那么仅考虑t∈(0,λ)的情况，有F(0)＞ 0＞F(λ)，又因为F(t)连续，因此必然存在某个点t′∈(0,λ)使F(t′)=0。

假设阈值初始值为t0，根据FlowMine 算法，由t0得到F，进而由F估计α，记α0=fF(t0)。由于F中节点的转发间隔均小于t0，因此，。由于随着阈值tn的减小，对指令转发参数αn的估计随之减小，将tn、αn代入式(4)，得到

考虑式(5)和式(6)，两者的差值仅在于α，现在分析指令转发服从指数分布的情况，即f(t|a)=ae-at。容易验证，当α=t时，函数取得最大值，且在区间(0,t)单调递增，在区间(t,∞)单调递减。因此，有

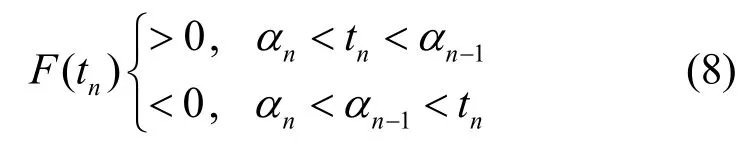
再结合式(8)及F(t)连续单调递减，可得

这样，对阈值t的估计可以收敛到真实值附近。因此，当给定一个初始阈值，随着迭代次数增加，tn依次递减，依次递增，达到相应阈值后，tn的单调性被破坏，此时，tn便在真实阈值附近稳定地波动，因此算法收敛。幂律分布的相关证明与上述证明过程类似。

证毕。

FlowMine 算法的收敛性也可以从图3 中看出，当t′取值变大时，算法1 中得到的F中节点间信息转发的平均间隔变大，从而导致估计的变小，由此估计出的阈值t′变小；而当t′取值变小时，从算法1 中得到的F中节点信息转发平均间隔变小，导致变大，由此估计出的阈值t′变大。

需要指出，当一个节点具有多个父节点时，单位时间内，其会收到多条来自不同父节点的多条指令，这样，该节点会相对比较繁忙，有可能会导致该节点观测到的平均转发间隔与指控信息转发间隔接近，甚至更小。对于这种情况，通常难以区分节点发送的信息是指控信息还是正常通信，尤其在无法知晓通信内容的情况下，至今没有有效的办法。

4 实验分析

本节首先通过模拟数据对文中的定理进行仿真验证，然后对FlowMine 算法的性能进行分析，最后将算法应用于实际数据，对实际数据中的信息流进行挖掘并分析。

4.1 模拟数据仿真实验

实验中，首先采用Kronecker Graph[17-18]来生成真实的有向网络结构，节点之间的指控信息将在网络的有向边上传播。该网络结构通常代表了节点之间的组织关系，比如上下级关系、指挥关系等。本文考虑了随机图（Kronecker 参数矩阵为[0.5,0.5;0.5,0.5]，后文实用Random 代表该模型）[19]、层次社区结构（Kroneckev 参数矩阵为[0.962,0.107;0.107,0.962]，后文使用Hierarchical 代表该模型）[20]及随机幂律树（后文使用Random-Tree 代表该模型）[21]这3 种不同的网络结构。每次在网络中随机选择一个节点作为起始节点，该节点将一条信息以一定概率随机发送给其子节点，收到信息的子节点将按照2.3 节中的模型，将信息在网络中传递出去，由此可以得到一个指令转发的信息流。重复上述过程，便可以得到多条不同的信息流。为了模拟节点之间的正常通信行为，随机依次从网络中选择2 个节点，构成节点间的正常通信行为。根据2.2 节的模型，节点正常发送一条信息的行为满足泊松分布，因此在观测时间窗口中，均匀地选择一个时间作为节点背景通信的发生时刻[13]。本文将上述观测的指控信息及正常通信信息混合在一起构成实验中观测的节点通信行为时序集合。

实验中，设定指控信息与背景通信数量的比值为SN，通常SN 越低，说明实验数据中指控信息所占比率越低，那么还原出信息流的难度越大。为了衡量算法性能，本文采用了F1-measure[22]，其中查全率定义为算法识别出的信息流占实际信息流的比例，准确率定义为识别正确的信息流占全部识别出的信息流的比例。

按照上述设置，分别生成了64 个节点，75 条边的层次网络、随机图及随机树3 种不同结构的网络，并模拟生成了180 条指控信息在网络中随机传播，实验中每条边的传播概率设置为0.5，SN 设置为0.07。由于算法在估计阈值时，先估计α并不断迭代，因此如果α收敛，那么算法对阈值的估计将收敛。图4 展示了不同的指控信息转发模型下算法1 的收敛性情况。从图4 中可以看出，算法对于不同的模型、不同的网络结构均可以稳定在某个值附近。算法对于幂律分布的收敛性稍差于指数分布，幂律分布的波动性要大一些，而指数分布中估计值的波动非常小，但估计值均围绕某个中值进行波动。因此在实际的应用中，可以对算法1 的每次迭代乘以一个收敛因子，或者取每次波动的平均值作为估计值。图4(a)中算法对不同网络结构的α估计值基本上在真实值附近，差别并不大；而图4(b)中算法对不同网络结构的α估计值相差比较大。对于这种情况，本文认为是由于在不同的网络结构中，指令信息传播的范围有很大差别，这会明显影响到观测节点转发信息的平均时间间隔，而这对于阈值及α的估计会产生较大影响。从收敛速度上看，算法可以很快地收敛到稳定状态，基本上5 轮迭代就能够达到平稳的状态。

图4 不同模型下算法的收敛性分析

FlowMine 算法在不同模型以及网络结构下的性能如图5 所示。从结果中看，算法在SN=0.5 以上时均能够达到较高的F1-measure，虽然并没有完全准确地还原出所有指控信息流，但也能够达到一个可以接受的性能。算法对于幂律分布的还原性能要优于指数分布，这一点可以通过图4 来解释。算法虽然对幂律分布的收敛性不如指数分布，但其波动范围能够覆盖到其参数的真实值，这样，取均值后对于幂律分布参数的估计误差会小于指数分布的误差。因此，其在还原时可以达到更高的精度。从这一点可以看出，对模型参数的估计误差能够明显地影响到算法的性能，提高估计精度可以有效地提高算法性能。

实验表明，算法在SN=0.8 左右会有一点下降，其原因主要在于，算法中假设了指控信息数量远小于背景通信的信息数量，当SN 提升后，该假设造成的误差会大大增加，因此造成了算法性能的下降，而随着SN 的提升，指控信息的还原难度随之降低，因此，算法的性能在SN=0.8之后又提升了许多。

图5(b)中算法对于层次社区型网络结构的还原要差于其他2 个类型的网络结构，而图4(b)中算法对于层次型网络的参数估计误差是最大的，这从另一方面佐证了上述分析中参数误差对算法性能的影响。在图4(a)中，算法对几种网络结构的参数估计的均值均落在了真实值附近，因此，图5(a)中算法的性能相差无几。

图5 算法1 在不同模型以及网络结构下的性能

4.2 安然邮件数据集分析

本节通过对安然邮件集[23]进行分析，挖掘其中的指控信息流，并分析网络中指控信息的传播模式和特点。安然数据集是安然公司几千名员工办公邮箱中的邮件数据集合，最初由联邦能源局公开，由卡内基梅陇大学的William Cohen 收集并用于科学研究。本文使用了其中一个含有151 名标注了员工岗位职级的版本，由于仅需要邮件通信的双方及时间，舍弃了邮件的内容，仅提取了邮件的发送者、接收者及邮件发送时间，然后将这些数据存入MySQL 数据库中。本文选取了邮件集合中时间在2001 年1 月1 日—3 月1 日共2 个月的邮件，并手动标注了涉及指控信息流的邮件，统计结果如表1所示。

表1 数据集简介

为了验证FlowMine 算法所求阈值的性能，本文将参数ratio 与求得的阈值相乘，也就是假设判别指控信息流的阈值为FlowMine 求得阈值的ratio倍。通过对ratio 取不同的值，得到算法挖掘指控信息流的性能F1-measure，如图6 所示。

图6 FlowMine 性能分析

从图6 中可以看出，当ratio=1 时，求得的指控信息流最准确，这可以说明，FlowMine 对于阈值的估计在实际数据中相对是比较准确的，对指控信息流挖掘的F1-measure 可以高达0.8，可以认为其结果对该数据集是可信的。

将基于文献[2-3]思想提出的Disclosure 算法与本文的FlowMine 算法在安然邮件数据集中进行对比，挖掘指控信息流的PR（precision-recall）曲线如图7 所示。Disclosure 算法采用了流量大小、通信时间等多种属性特征来挖掘指控信息流。从图7所示的实验结果可以看出，FlowMine 算法在安然数据集中性能远优于Disclosure。

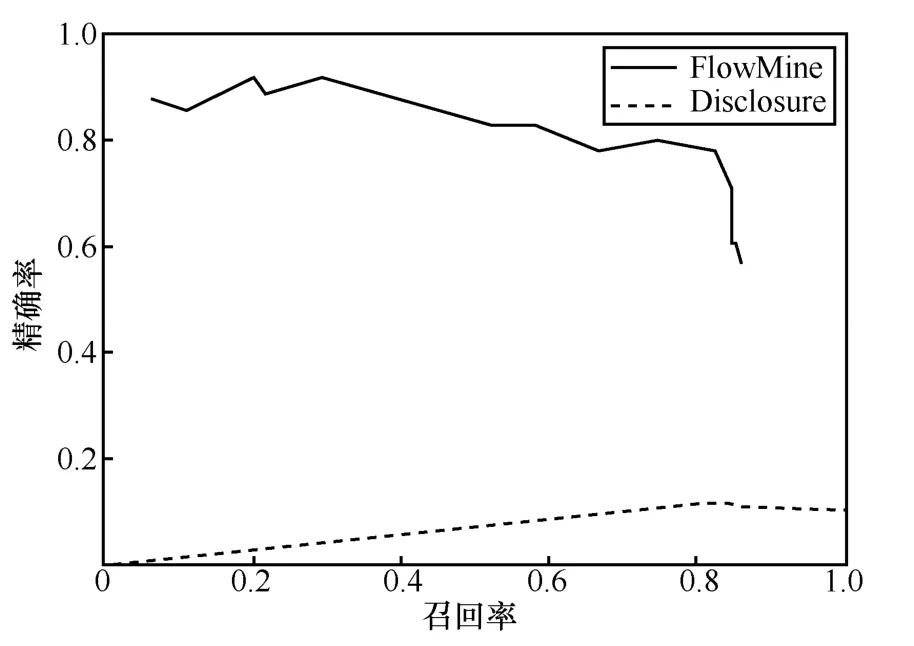
图7 安然数据中的算法性能对比

对安然邮件集使用算法1 挖掘其中的信息流，结果如图8 所示。图8 中的每个子图为挖掘出来的每条信息流，其岗位标注在了节点周围，未知的岗位采用NA 来表示。其中，有向边代表信息的流向，每条信息流存在一个根节点，代表信息的发起方，至少存在一个子节点，代表信息的流向。

图8 安然邮件集合中的指控信息流

从挖掘到的指控信息流可以看出，每条指控信息流的长度均不会太长，所发现的最大深度为4 层。最常见的信息流结构为星型和树形，通常是某个节点将信息传递给多个子节点，以达到信息扩散的目的。从人员岗位的组成上看，处于领导地位的节点通常位于信息流的末端，而一般信息流中的中间节点岗位通常为员工；仅有少数的信息流由领导发出，然后传播给其他员工。挖掘出的信息流中还存在着大量仅有2 个节点构成的信息流，尽管这些信息流在图中看起来很短，实际上，在2 个节点之间存在多次邮件的往来，这种情况一般是双方互相回复对方的邮件。通过对挖掘出的信息流邮件内容进行分析发现，星型结构中的中心节点的角色是秘书，其行为通常是将信息分发给他的上司；另一方面也会将领导的指令或任务传达给相应的员工。通过信息流的挖掘还发现，有的节点经常给自己发送邮件，这种情况一般是员工将重要信息留存到自己邮箱做备份，或是方便检索用，这个与员工的行为习惯相关。

通过上述分析发现，处于领导岗位的员工并不一定是信息的发起方，因为经常遇到这种下属将信息汇总并报告给领导的情况，因此，很难仅仅通过节点在信息流的位置来判断节点的身份信息。然而，通过对信息流的分析，可以发现很多节点的行为习惯，以及网络中信息传递的路径等。更进一步，可以断定同一个信息流内的节点在业务上至少是相关的。在星型结构中的中心节点通常是一个纽带的角色，这种节点的角色一般是秘书，其需要与上级和下级保持联系，因此在信息的传播路径中处于中心位置。

更进一步，可以知道在安然公司中，其组织相对扁平，因为通过邮件对信息的传播深度并没有超过4 层。尽管公司实际的组织结构并不知晓，但这一现象的原因可能是电子邮件拉近了人们之间的距离，因此管理上的层级更加扁平。

下面对所得到的指控信息流进一步分析，考察一些特殊的节点，比如sara.shackleton，这些节点出现在多个不同的指控信息流中。图9 给出了员工sara.shakleton@enron.com 在不同指控信息流中所处的不同位置，该节点在观测时间内一共出现在了4 个不同的信息流中，节点名称标记在节点上。容易发现，该员工与mark.e.taylor、tana.jones、stephanie及susan.balley 几名员工关系比较密切，该员工在信息流D 中处信息流末端位置，与员工susan.balley、stephanie 等一起收到了mark.e.taylor 的信息；在信息流C 中，该员工收到mark.e.taylor 的信息后将信息转发给了tana.jones 以及susan.balley 等，在信息流B 中，该员工与tana.jones 进行了信息的交互，并一起将交互的信息传递给了其他几名员工；在信息流A 中，该员工收到stephanie 的信息后转发给了susan.balley 等，通过这几个信息流，可以初步推测该员工要比 mark.e.taylor 等级低一些，且与susan.balley、tana.jones、stephanie 这几名员工等级相同。更进一步发现，susan.balley、tana.jones、stephanie 及sara.shackleton 这几名员工多次共同出现在几个不同的指控信息流中，那么可以推测这几名员工应该属于同一个部门，但是这几名员工的身份信息应该是不同的。在信息流D 中，mark.e.taylor处于中心节点位置，而且该节点与该部门多个外部节点有联系，可以推断mark.e.taylor 不属于该部门。mark.e.taylor 一次性给sara.shackleton、susan.balley和stephanie 这3 名员工同时发送信息，该行为可以推测为一次信息的下达过程。sara.shackleton 在信息流 A、B 以及 C 中均处于中心位置，其收到stephanie、tana.jones 及mark.e.taylor 的信息后对其他的员工进行了信息的广播，从这个信息流中推测，sara.shackleton 的角色比较类似于部门的中转者或者操作员，负责一些信息的传达等。

图9 单个员工在指控信息流中的情况

以上是在不知道任何一名员工的职位的情况下仅通过挖掘出的指控信息流做出的一些推测。通过对邮件的内容进行确认后，可以证明上述的这些分析。尽管数据集中没有对这几名员工的职位进行标注，但是，通过对用户在不同指控信息流中的分析可以发现一些额外的信息，并能够推测出mark.e.taylor 等级要高于sara.shackleton，以及sara.shackleton 的同部门同事有哪些。

但是这些分析仍然具有一些局限性，本文只是随机挑选了sara.shackleton 这名员工，其他员工的情况还需要更进一步地分析才能得到更多、更准确的信息。如果只分析几名员工的指控信息流，又容易造成“盲人摸象”的情况，信息流中的其他用户的行为难以体现在这些指控信息流中。

4.3 实验总结

本节首先通过模拟数据对算法的性能进行了分析，验证了本文提出算法的收敛性。对算法的性能分析中，采用了F1-measure，在低信噪比的情况下算法能够达到约0.8 的水平，这说明算法具有较高的准确率与查全率。然后使用该算法对安然邮件集合中的节点通信行为进行分析，并根据挖掘出的信息流对节点的属性及网络的信息传播路径等进行了分析。分析后发现，公司中处于领导地位的节点并不一定是信息的发起节点，而是有时会由秘书将信息汇总给上级。其次，信息流的中心节点一般是秘书之类的角色，其不仅将信息汇总给上级，而且还会将上级的任务或指令传达给下级相应人员。从信息流的长度看，电子邮件有效地拉近了上级与下级的距离，并使公司的网络更加扁平化。

更进一步，通过分析同一名员工在不同指控信息流中的情况，能够挖掘出更加深入的一些信息，比如员工间关系、等级等。通过对邮件内容的确认，验证了算法挖掘出指控信息流的有效性。

5 结束语

本文研究了通信网络中节点的通信行为，并对节点的正常通信行为和指令转发行为分别进行了建模。然后提出了FlowMine 算法对模型的相关参数进行估计，提取节点的指令转发行为。在实验部分，首先通过模拟数据和实际标注的数据对算法的收敛性和性能进行了评估，然后将FlowMine 算法应用于安然邮件集合，并对网络中节点的行为和角色进行了分析，验证了算法的有效性。

尽管本文已经实现了网络中信息流的挖掘，并取得了许多有意思的结论，但是对于该方面的研究还存在许多问题，把握节点的指控信息流具有一定的局限性，还需要一种手段将这些不同的信息流进行综合处理，得到目标网络中用户间信息的传递模式，这样才能从整体上对网络及用户进行把握和分析。