遗传与禁忌搜索算法组合的停机位优化分配

孙淑光，张泰荣

（中国民航大学电子信息与自动化学院，天津 300300）

机位分配是一个多约束、多目标的组合优化问题。目前机场以人工分配为主，依靠经验对停靠的飞机进行机位分配，导致效率低下、成本较高。当飞机数量和机位数量达到一定程度时，较难得到一个高效合理的分配方案，而如果分配不合理，则会严重制约机场的运行[1]。机位分配属于NP-hard 问题，传统方法难以解决。专家系统法[2]、分支定界算法[3]只能提出单个分配方案，并不实用，而启发式算法[4]如遗传算法（GA,genetic algorithm）、禁忌搜索算法（TS, tabu search）、蚁群算法（ACO,ant colony）、模拟退火算法（SA,simulated annealing algorithm）等均适用于解决该类问题。遗传算法具有收敛性好、全局搜索能力强的优点，但该算法容易陷入“早熟”，因此需要二次启发。田晨等[5]以机位空闲时间方差最小化作为优化目标；戴顺南[6]以航班等待延误时间和机位使用空闲时间为优化目标建立模型；卫东选[7]以最小化停机位各空闲时间段的离差为目标函数建立数学模型；冯程等[8]建立了降低旅客进出机场飞行区时间的停机位分配模型；徐浩[9]以总的延误成本最小为目标函数，采用改进遗传算法进行求解。但上述研究优化目标过少，很难符合实际情况，且在实际分配中航班存在不同优先级的情况，而之前的研究更多是以先到先分配为原则进行分配。

通过设计新的目标函数并加入优先级的概念，将遗传算法与禁忌搜索算法组合，通过遗传算法求出一组可行分配方案集合，然后通过禁忌搜索算法对该分配集进行优化。

1 模型建立

停机位分配涉及到的因素较多，包括机型大小、机位大小等。为方便研究，做出如下假设：

1）信息已知化 在预分配前，对当天停靠飞机的所有信息如机型、降落时间、起飞时间、航班信息等均假设已知；

2）时间有限化 由于机位分配是一个动态过程，如果不设定时间段很难求出最优方案，因此，需要假设只分配一个时间段内的飞机，方便求出最优分配方案；

3）容量许可化 假设机场机位足够所有飞机停靠，即不会出现机场超负荷的状况。

由于在实际分配过程中会出现紧急情况，部分飞机拥有更高的优先级，先到先分配原则的实用性受到影响，因此，将按照飞机优先级进行机位分配。要对机位分配进行优化，首先需要对其进行数学建模，定义变量[10-11]如下：

飞机集合P={Pj|1≤j≤n}表示在一个时间段内需要分配机位的飞机；

机位集合S={Si|1≤i≤m}表示在一个时间段内机场可提供的机位；

Eij表示Pj进入Si的时间；

Lij表示Pj离开Si的时间；

Td表示两架飞机被安排停靠在同一机位之间相隔的安全时间，Td＞0；

Dj表示Pj可分配机位集合；

状态变量Yij∈{0，1}，当Si被分配给Pj时，Yij=1，反之为0；

Ti表示Si总空闲时间的平方和，即

其中：k 表示被分配到Si的飞机序号；Ni表示停到Si的飞机数，且Ei(k+1)-Lik≥Td；

T 表示所有机位总空闲时间的平方和，即

PZ 表示飞机机型的大小集合，PZ∈{3，2，1} 分别代表大、中、小型机型；

SZ 表示机位的大小集合，SZ∈{3，2，1} 分别代表大、中、小型机位；

PZj表示Pj的尺寸，PZj∈PZ；

SZi表示Si的尺寸，SZi∈SZ；

Fj表示Pj分配给Si的占用效率，Fj=PZj/SZi；

F 表示分配方案中所有飞机的总占用效率，

在停机过程中，为防止某些机位使用过度，某些机位使用过少，造成机位使用的不均衡，应将机位空闲时间平方和的最小化作为目标函数之一。此外，如果机位大小与停放飞机的大小不匹配，也会造成资源的浪费，使停机成本增加。因此，优化目标综合考虑上述两方面因素，目标函数同时包含机位的占用效率最大化。

所以设立目标函数为

f=-ω1T+ω2F

其中：ω1为机位空闲时间平方和的权重；ω2为占用效率的权重。由于空闲时间与占用效率不属同一量纲，应做归一化处理，即

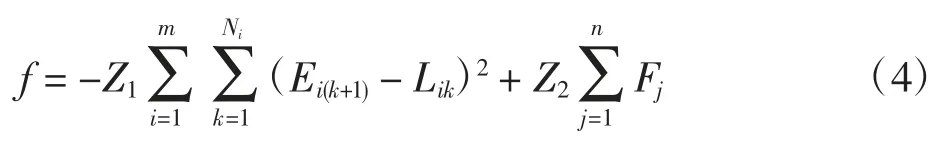
其中：Z1=ω1/Tmax；Z2=ω2/Fmax；Tmax为理论上所有机位最大空闲时间的平方和；Fmax为理论上最大占用效率。

因此，停机位分配优化的目的是求f 的最大值，即

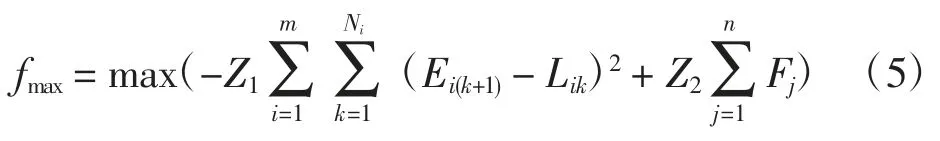
2 程序设计

2.1 基于优先等级的基因编码

机位分配优先级具体为：国际航班优于国内航班，其优先级别最高，不考虑其他因素；当同为国内或国际航班，大型飞机优于小型飞机[6]；当同为国际或国内航班且机型机同，先到飞机优于后到飞机。

采用实数进行编码，先将飞机以优先级高低进行排序，Pj优先级计算如下

其中：nj表示Pj对应的航班是否为国际航班；Emax表示在一个时间段内理论上最晚降落的时间，Eij和Emax均进行有理化转换为整数值；K1、K2、K3为系数，根据优先级的条件确定。

每条个体中序号代表飞机优先级序号，对应的赋值代表机位id，如图1 所示，从0 位开始，第2 位表示将优先级为2 的飞机分配到4 号机位（序号越小，优先级越高）。

基于遗传算法生成一组分配方案集的流程如图2所示。

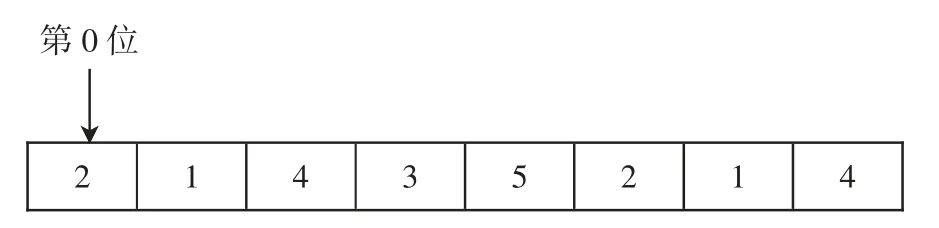
图1 飞机机位基因编码Fig.1 Gene coding of airport gate

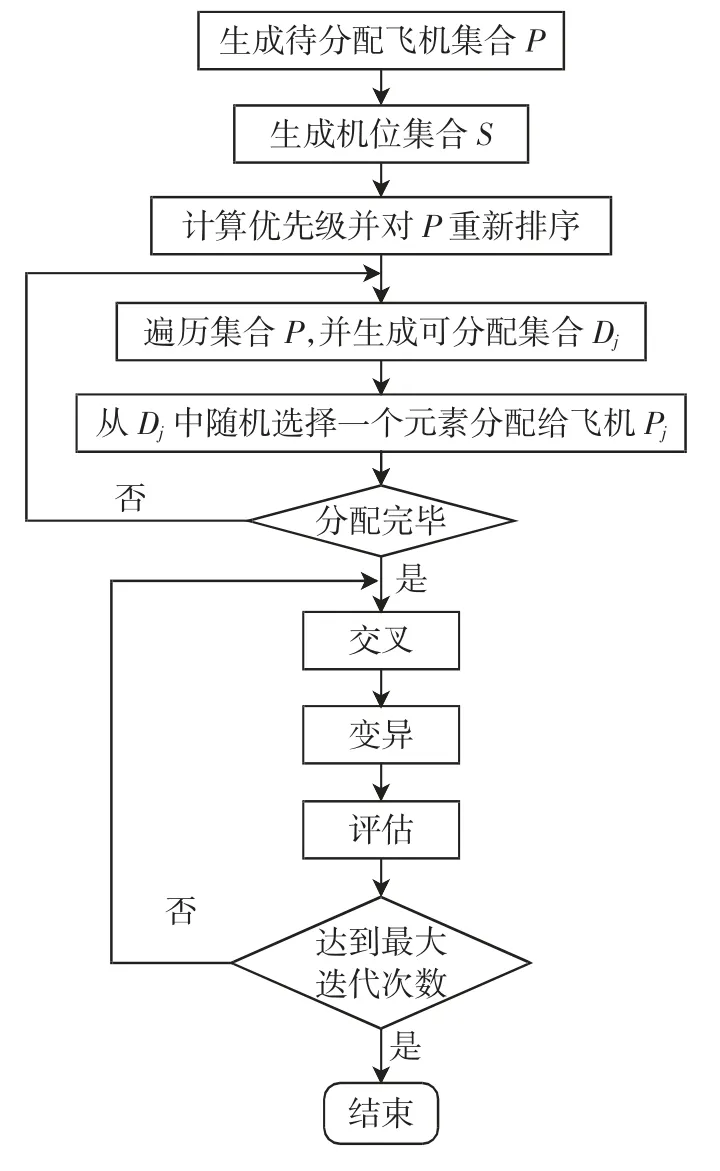
图2 基于遗传算法的机位分配流程图Fig.2 Flow chart of airport gate assignment based on GA

2.2 初始解生成

为提高初始解的生成效果，按如下步骤生成初始分配方案：

1）生成Pj的可分配机位集合Dj，可行性判别标准有PZj≤SZj，飞机使用机位的时间不与该机位分配给其他飞机的时间冲突；

2）随机从可分配集合Dj中选一机位分配给Pj；

3）更新该分配机位的占用时间段；

4）重复此操作直至所有飞机分配完毕。

由于生成一架飞机的机位集合受之前分配影响，若某一飞机的可分配机位集合为空，则只能将该飞机分配到停机坪。

2.3 选择

采用轮盘式选择，每条个体所对应的适应度函数值越高，则被选中的可能性越大。第k 条个体被选中的概率POSk如下

其中：fk为第k 条个体对应的适应度值；N 为种群容量。

2.4 交叉

采用自适应交叉率[12]，每条个体都以一定的交叉率进行交叉运算。第i 条个体交叉率Pci的计算如下

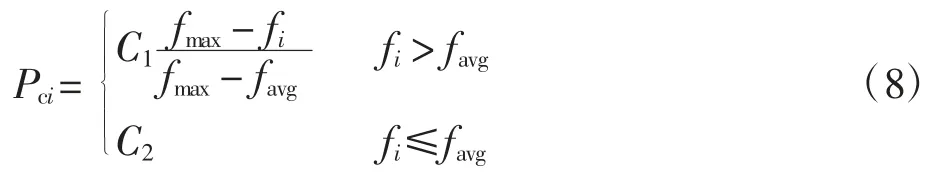
其中：C1、C2为小于1 的正数；favg为种群的平均适应度值；fmax为种群中最大适应度值；fi为第i 条个体的适应度值。

交叉运算采用两点交叉[13]，通过选择过程选出父代母代，随机生成两个交叉点a、b。ab 之间的部分就是需要交换的部分，如图3 所示。

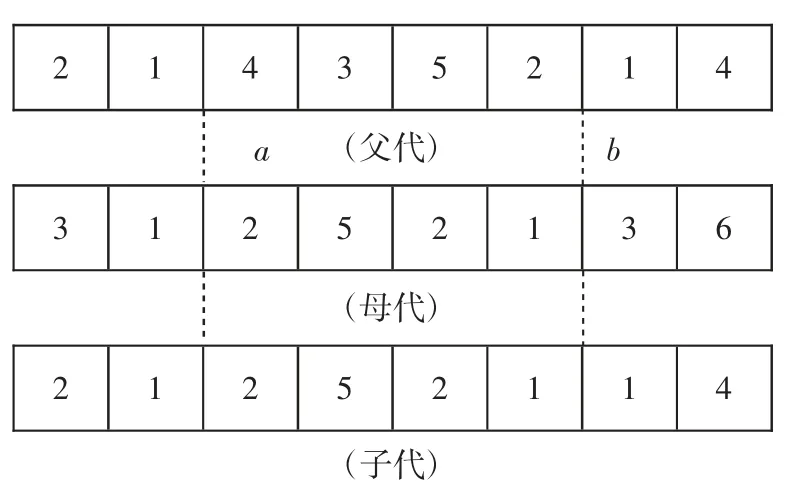
图3 交叉运算操作Fig.3 Crossover operation

为方便描述，设开始到a 点之前的基因称为A段，b 点之后到结尾的基因称为B 段，a、b 之间的基因称为ab 段。先将A 段和B 段父代基因赋给子代相应的位置。由于母带ab 段的分配可能会与子代A、B 段分配在时间上产生冲突，产生无效解，所以应做检错处理，具体过程如下：

1）去除父代ab 段中对应分配给飞机机位的占用时间段；

2）在母代中ab 段中每一位做如下操作：①判断该位是否冲突，若不冲突，则将母代对应位的分配赋给子代，更新子代该机位的占用时间段并判断下一位；②若冲突，则清空该飞机的可分配机位集合，重新生成该机位的可分配机位集合，从该集合中选择一个机位分配给该飞机。

3）将交叉后的子代个体替换父代个体。

2.5 变异

同交叉过程，采用自适应变异率，每条个体都有一定概率进行变异运算，即

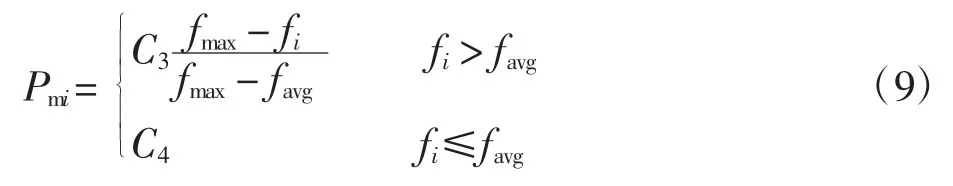
其中，C3、C4为小于1 的正数。

变异过程中，首先删除一架飞机对应分配给其机位的机位占用时间，清空该飞机对应的可分配机位集合，并重新生成该集合。若该机位集合为1，则分配给其该机位，然后重新选择基因，重复上述操作直至机位集合大于1，并重新进行变异运算；若不为1，则选择一个与原先分配机位不同的机位分配给该飞机。

3 二次启发

虽然遗传算法具有很好的全局搜索能力，但局部搜索能力较差。由于遗传算子中的交叉算子使得染色体之间具有很大的相似性，可能导致搜索停滞，种群多样性得不到补充，从而出现“早熟”的特征。而禁忌搜索算法具有很好的局部搜索能力，将遗传算法和禁忌搜索算法组合使用会起到很好的效果。具体方案为通过遗传算法生成最终种群后，将该种群通过禁忌搜索算法对其进行优化，之后选择种群中适应度值最高的个体作为最终分配方案。这种混合策略有效地结合了遗传算法极强的并行搜索能力和禁忌搜索算法出色的局部搜索能力。禁忌搜索算法的基本过程为：通过初始解产生一组邻域解，然后在邻域解中确定一定数量的候选解；若最佳候选解对应的目标函数值优于当前最优解，则忽视其禁忌准则，将该候选解替换为当前解和当前最优解，并将相应的对象加入禁忌表；若不存在上述候选解，则在候选解中选择非禁忌的最优解为新的当前解，而无视它与当前解的优劣，同时将相应的对象加入禁忌表；如此重复上述迭代搜索过程，直至满足停止准则。具体流程图如图4 所示。

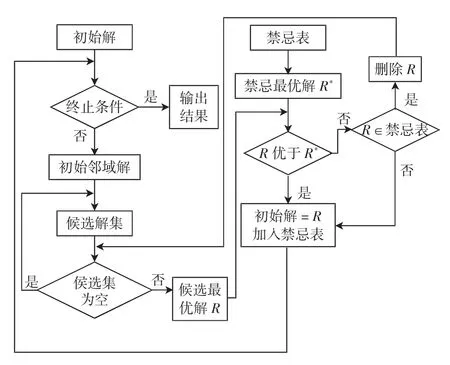
图4 禁忌搜索算法流程图Fig.4 Flow chert of TS algorithm

4 仿真结果及分析

采用首都国际机场的数据作为仿真实验数据。取时间段为0～24 点，需要分配的飞机架次为1 500 架，可用停机位数量为250 个。表1 为某日首都国际机场航班表（8：00～8：30），已将其按优先级进行排序。

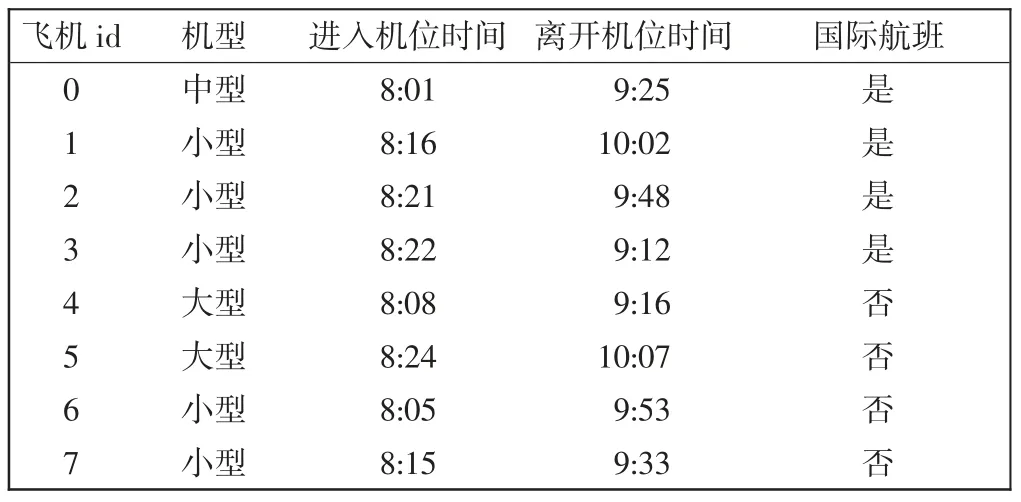
表1 某日首都国际机场航班表Tab.1 Flight schedule of Capital International Airport on one day

利用遗传算法进行优化分配时，取交叉率C1=C2=0.7，变异率C3=C4=0.05，最大迭代数为100，种群数量为50，适应度函数中ω1=ω2=1。通过随机数对初始种群进行赋值，仿真结果如表2 所示。

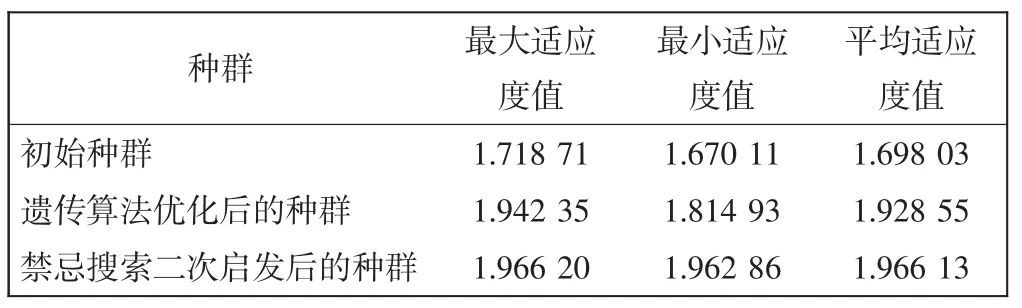
表2 仿真结果Tab.2 Simulation result

最终分配方案即为通过二次启发后最大适应度值。其中，结合公式（1）～（4），可知其对应的机位总空闲时间为113.73，实际有效分配机位的飞机架次为1 418，即每个航班与停机位类型的匹配程度为0.945 33（越接近1说明越匹配）。从表2 可看出，初始分配中最优解对应的目标函数值为1.718 71，通过遗传算法优化后达到了1.942 35，增幅为13%，而通过二次启发后目标函数值达到1.966 20，增幅为14.4%。遗传算法取得较好的效果，禁忌搜索算法二次启发后的分配效果比遗传算法有进一步提升，改进的遗传算法可给出更加优化的机位分配方案，具有高效、实用的特点。

5 结语

在综合考虑机型大小、机位大小、进入机位时间与离开机位时间、飞机优先级等因素的情况下，充分考虑实际情况，建立机场停机位分配模型，提出优化目标函数，采用禁忌搜索二次启发后的遗传算法，提高了目标函数值，并通过实例对模型进行了仿真测试。结果表明，相比随机分配，遗传算法优化效果明显，而结合禁忌搜索算法优化后，优化效果进一步提高。