基于ADS-B数据挖掘的4D航迹预测方法

马 兰，高永胜

（中国民航大学空中交通管理学院，天津 300300）

4D 航迹是航空器在时空上的运行轨迹，包含其所在位置的经度、纬度、高度的三维坐标在时间轴上的变化。新一代空中交通管理系统通过各空域流量的匹配和优化、冲突探测与解脱技术，航班排序和调度手段等来辅助空管人员进行决策，均离不开对航迹的精确预测。航空器的4D 航迹预测即推算航空器在将来一段时间内飞行的4D 轨迹，主要为了维持航空器有序运行、保证空中交通系统安全和提高空域流量等。

鉴于4D 航迹预测在空中交通运输系统的重要性和迫切性，国内外学者对此研究进行以下尝试：文献[1-2]基于雷达数据建立的运动学模型预测4D 航迹，解决了其他预测模型参数过多的问题；文献[3]提出了基于隐马尔科夫模型的自适应参数选择轨迹预测模型，并在给定的航迹数据参数中选出最优的预测模型；文献[4-5]根据基本飞行模型进行航迹研究，仅得出航迹特征点和到达航迹特征点的时间；文献[6-8]重点针对终端区4D 轨迹来控制和优化飞机的程序轨迹，从爬升段和进近段设计航空器飞行程序进行预测；文献[9]在等角飞行航迹的基础上，运用卡尔曼滤波（KF）和扩展卡尔曼滤波（EKF）联合算法确定航空器的地速，以此推断航空器过点时间，此方法对于短期航迹预测效果较佳。以上研究多基于运动学模型或基本飞行模型，有以下几点不足：①气象因素难以完全模拟，已有成果多是将整个飞行轨迹划分为若干阶段，再利用数学模型对各阶段的飞行情况建模，而在航空器飞行全过程中，诸多动力学参数，如大气阻力、风速风向、大气密度等瞬息万变，很难精确预测；②基于单一数学模型的预测过于理想化，忽略了诸多影响因素，如地面管制、空域限制等；③航班飞行计划与实际航迹有偏差，由于实际飞行情况经常不完全依据之前制定航路运行，从而造成预测航迹和实际航迹的水平方向偏离过大。综上所述，大部分模型在航迹预测研究中均存在缺陷、精度不高等问题。

鉴于飞机性能模型和空气动力学模型在预测中出现的较大误差，提出一种基于ADS-B 数据挖掘的建模思路。此模型不依赖运动学或基本飞行模型，完全基于航班的历史数据，参考飞行计划给定的数据，拟合出基于历史数据的标称航迹并进行预测，解决了预测精度不高的问题。

1 ADS-B 数据预处理

广播式自动相关监视（ADS-B，automatic dependent surveillance broadcast）通过发送报文获取航班飞行参数，具有周期性和自发性。报文信息主要包括ICAO 地址、经纬度、高度、航向、速度、时间等，目的是便于管制人员和其他航班对某航班状态进行监视。ADS-B 的数据存在一些干扰数据和缺损数据，在进行数据分析前，需要将其剔除。

1.1 ADS-B 数据线性插值

ADS-B 数据周期约为1 s，因此，每次航班的数据轨迹都是由若干个航迹离散点构成。在ADS-B 数据处理研究中，将原始航班数据直接运算并进行分析预测，会造成较大的位置误差，故在运算前先运用数据插值算法对原始数据进行预处理。

对ADS-B 原始数据进行筛选前，首先将原始数据依据ICAO 地址码、航班号和飞行时刻进行分别标记，从而得出航班数据的累积轨迹点序列。其中，每条ADS-B 数据所包含的重要数据信息如下：p={标记时间，经度，纬度，高度，地速，航向，垂直速度}。设该航班的累积轨迹集为

T={t1，t2，…，tn}

其中：n 为选定时间内的总轨迹条数；ti为航班第i 条的飞行轨迹，每条ti都是一个间隔约为1 s 的有序排列的时间点序列，M 表示轨迹ti中含有数据点的个数。

将累积轨迹集T 中所有的飞行数据轨迹ti依据标记时间和经纬度进行归一化处理，使该序列完全分布到时间片段[0，1]上，然后依照设定的时间粒度参数，再采用线性插值函数对ti插值计算，最后把轨迹集T 中的所有轨迹剪切为等长序列（即数据点个数M 相同），从而生成新的轨迹集。

1.2 数据过滤

由于飞行数据受天气、流量控制等因素影响，样本中错误数据较多，传统防脉冲干扰平均滤波法仅能过滤掉最大最小极值，并不能完全剔除错误数据，因而提出了改进的防脉冲干扰平均值滤波算法。

该算法基本思想如下：

1）先连续采Z－1 个航迹段：t1*，t2*，…，tZ-1*；

2）采入一个新的采样航迹段ti*（i≥Z）；

4）在Y1，Y2，…，YZ，Z 个样本值中过滤掉A 个极大值和A 个极小值，然后对余下的Z－2A 个样本值求平均值即

5）判定采样过程是否终止：若采样样本量足够代表样本总量的总体趋势，则采样过程结束；否则转至步骤2）继续采样。

改进后的滤波算法过滤掉了A 个极大值和A 个极小值，若A 值在合理区间内，那么A 取值越大，此算法的优势就越显著。综合考量样本数据的跟随性，A 的取值不能太大，优化后的算法提高了滤波的抗干扰能力，为后续的研究提供可靠数据。

2 数据处理及航迹预测

2.1 基于修正欧氏距离的飞行轨迹相似度计算

在等数据量的轨迹集T*中任选2 条轨迹和，首先采用逐点法算出等角航迹距离，再使用均值方法衡量2 条轨迹间欧式距离的相似度，两轨迹间欧式距离越小表明两轨迹间的相似度越高。鉴于原始航班数据中存在少量数据噪声，对航迹距离计算结果有一定影响，所以数据降噪处理是数据分析处理的必要前提。

参考航空器在航路范围内的飞行特点，取2 条轨迹距离的方差和航向做比较，同时对上述结果进行修正，算法过程如下。

其中：D（X）代表轨迹间距离集合的方差；Δ是2 条轨迹间相似度的修正值。

综上，可得到轨迹集的相似度矩阵为

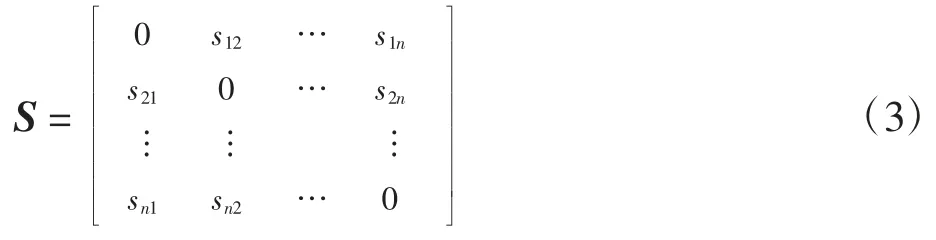
2.2 飞行轨迹的降噪处理

由于噪声对不同类型的航空器的影响程度不一样，为排除噪声的影响，保证聚类和预测结果的科学性，采用高斯核函数对上述计算结果相似度进行平滑降噪处理，即

其中，sij是轨迹和轨迹的欧氏距离相似度，σi和σj为轨迹和轨迹的规模参数，代表该条轨迹的规模特征。

根据文献[10]的理论，结合航空器的ADS-B 数据特点，得出适应于ADS-B 数据的规模参数选取方法。选取距离某轨迹最近邻范围为y 内的最大距离为规模参数。定义轨迹的相似度集合为Si={si1，si2，…，sin}，则σi表示为

式中，r 是一个独立参数，通过多次试验验证，取r=10。

2.3 终端区CURE 聚类算法预测航迹

每条航迹是由离散点构成，且各条航迹的离散点数量也不同，不存在典型的数据与属性之间的对应关系，故选用基于层次聚类的方法对轨迹集T*的航迹数据进行航迹聚类分析并预测。采用CURE（clustering using representatives）算法[9]实现航迹聚类预测的2 个明显优势：①CURE 算法不必随机选择聚类中心，可避免陷入局部最优；②该算法使用中心点和代表点来表示聚类的结果，从而为后续研究飞行轨迹提供可靠的数据基础。CURE 的航迹聚类算法如下。

输出:航迹聚类结果C={C1，C2，…，Ck}，航迹聚类中心AVE = {ave1，ave2，…，avek}，以及代表点的航迹Qe={Qe1，Qe2，…，Qek}。

1）利用基于修正欧氏距离的航迹相似度算法计算T*中任意2 条航迹之间的相似度，构建航迹相似度矩阵ST*。

2）初始化聚类。每条航迹都是一个初始的独立类，构建动态数组clusters 并存放聚类结果，clusters 中含有n 个初始类，每类中包含1 条航迹。

3）当聚类结果clusters 中类个数大于k 时，进行以下步骤：

a）根据航迹相似度矩阵ST*，获取相似度最大的2条轨迹;

b）标记2 条航迹的当前所属类，分别定义用Cα和Cβ表示;

c）分别计算类Cα和Cβ的中心航迹aveα、aveβ和其代表的航迹集Qeα、Qeβ，同时判断这2 条轨迹是否为当前所属的聚类代表航迹之一；

d）若2 条航迹不属同一类，且均是各自当前所属类的代表航迹时，那么合并类Cα和Cβ，生成一新的聚类Cδ，同时clusters 中类的个数减1;

e）更新聚类Cδ的中心航迹aveδ和代表航迹集Qeδ。

4）输出航迹的聚类结果C={C1，C2，…，Ck}，每个类的中心航迹AVE={ave1，ave2，…，avek}和代表航迹为Qe={Qe1，Qe2，…，Qek}。

CURE 聚类得到的聚类航迹一定程度上表示了航班运行的总体趋势，可作为典型航迹用于4D 航迹预测，也可用于研究航迹趋势变化和相对应的管制意图等。若要利用历史航迹数据预测下次航班任务的航迹位置信息，可用聚类结果在时刻τ 的位置信息进行航迹修正，即可预测下一时刻τ+h 的航班位置信息，即

其中：h 为预测时间步长；Cp为预测航迹；Cc为聚类航迹；CR为真实航迹；ε（τ）为聚类航迹与真实航迹在时刻τ 的航迹修正。

3 算例验证

为验证基于ADS-B 数据挖掘的4D 航迹预测的合理性，收集天津地面ADS-B 数据进行试验。在数据中以青岛—北京CDG4651 次航班为例，研究利用2017年1～5 月的ADS-B 数据，提取该次航班的轨迹并进行降噪处理，如图1～图2 所示，再对航迹进行预测，如图3～图4 所示。将预测航迹和6 月1 日此航班的实际飞行轨迹作对比，对比内容包括经过重要航路点的过点时间，过点高度等，结果如表1 所示。

图1 CDG4651 次航班航迹聚类提取Fig.1 CDG4651 flight trajectory clustering extraction

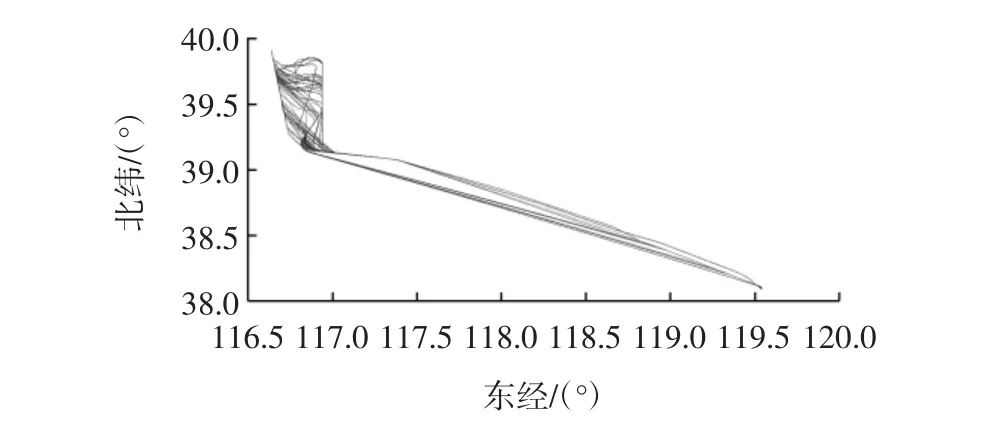
图2 滤波及降噪后的航迹Fig.2 Filtering and de-noising trajectory

表1 过点时间、高度预测结果比较Tab.1 Comparison between actual and predicted past time and altitude

图3 中CDG4651 次航班的航路轨迹比较稳定，而图4 中终端区轨迹由于进近管制和进场间隔的因素而显得杂乱，在研究时把终端区航迹聚类分析，通过天气、管制等因素的影响来确定选定航班的标称航迹，从而达到精确预测效果。但在实际飞行中，由于风向、交通管制及终端区等待等情况，航空器在终端区的轨迹明显的分为2 个路径，分别进行预测拟合，得到2 条终端区预测航迹。预测航迹在和6 月1 日此航班的实际飞行轨迹对比可看到，过点时间误差基本在30 s 之内，过点高度误差不超过50 m，非常接近实际值。由此可见，模型的预测结果精度较高。

图3 航路部分航迹预测Fig.3 Partial route trajectory prediction

图4 终端区部分航迹预测Fig.4 Terminal area trajectory prediction

4 结语

基于ADS-B 历史数据挖掘的航迹预测方法，适用于实时性较高的空域管理系统，其预测航迹可为管制人员提供参考。结果表明，该方法能较为准确预测出4D 航迹，对实际飞行具有一定参考作用，但由于该方法需要大量的ADS-B 飞行数据，且需要针对不同机型不同航路建立相应的数据库，实际操作工作量较大。