跨栏中的数学模型
杨卓桥


摘要:数学来源于生活,应用于生活,而数学模型则是其中的桥梁。运动轨迹模型是数学模型中最常见的模型之一。跨栏属于田径运动,其要求在一定距离内,跨过一定高度和数量的栏杆。研究跨栏中的数学模型不仅有助于运动员取得更好成绩,而且还能发现生活中的数学世界。文章从跨栏运动出发,通过数学公式推导,在考虑空气阻力和不考虑空气阻力两方面,对起跨距离、起跨角以及后蹬作用时间等方面进行分析,并得出结论。文章提出的跨栏数学模型也可以运用于机器人对于角度和距离的选择上,从而让机器人能够更好地对角度以及距离做出最优判断。
关键词:空气阻力;运动轨迹模型;运动的分解;力的分解
一、问题背景
18世纪前后,英国的畜牧业相当发达,牧民跨越畜栏追赶牲畜是基本的生活技能。年轻人把栅栏搬到平地上,设置若干个障碍物,谁能跑在最前面,谁就能赢得奖励,这是跨栏运动的雏形。
跨栏运动是速度与技术的完美结合,随着科学技术的发展和训练水平的提高,竞争也越来越激烈,对运动员各方面素质的要求也越来越高,为使运动员能够更加科学地运用跨栏技巧,现提出以下有待深入探究的问题。
1.如何选择跨栏时起跨角;2.起跨距离对跨栏会有什么影响;3.后蹬作用时间对跨栏会有什么影响;4.到达起跨点的瞬时水平速度对跨栏会有什么影响。
二、模型假设
1.不考虑栏间平均水平速度对跨栏的影响;2.不考虑风速对跨栏的影响;3.人体重心位置是人体的黄金分割点;4.人体在栏杆正上方时重心位置和欄杆距离不变;5.空气密度、空气阻力系数不变;6.人为质点,质点位置即为重心位置。
三、模型建立与问题分析
跨栏可以看作是质点做周期性抛物线运动,在实际中有许多影响跨栏的因素,为了探讨这些因素,可以通过建立运动轨迹数学模型,利用运动的分解、力的分解、二次函数以及物理的其他相关知识,得出跨栏与起跨角的初步关系。
根据图1,设定以下参数(核心自变量V0、S0、t)。
h:栏杆高度
h0:人体重心高度(取人体的黄金分割点)
h1:人体重心高度与栏杆顶最小距离
g:重力加速度
m:人体质量
A0:人体直立时的正面面积
V0:到达起跨点的瞬时水平速度
S0:起跨距离
f:后蹬反作用力
t:后蹬作用时间
t0:起跳到达最高点的时间
F′:空气阻力
c:阻力系数
ρ:空气密度
θ:起跨角
通过查阅资料可得到以下关于栏架高度的数据:
女子100米栏的栏架标准高度0.840m;
女子400米栏的栏架标准高度0.762m;
男子110米栏的栏架标准高度1.067m;
男子400米栏的栏架标准高度0.914m;
本文选择男子110米栏进行分析,即栏架高度h取1.067m。
(一)在不计空气阻力的情况下
首先由f,θ,得到f在水平方向上的分力Fx大小为:
Fx=f*cosθ (1)
f在后蹬作用时间t内,所对应的Fx产生的后蹬水平速度为Fx*t/m,则此时水平方向速度为:
Vx=V0+Fx*t/m(2)
假设从起跳离开地面开始计时,用t0表示到达最高点的时间,若当最高点在栏杆正上方距离h1处为要到达的最佳点,则可用以下公式表示t0与高度的关系:
由公式(3)可知,起跳后到达最高点的最佳时间为:
由公式(1)、(2)、(4)可知,起跨距离为:
1. 通过改变S0,得出S0与θ的关系
假设到达起跨点时的瞬时水平速度V0=5.0m/s,f为800N为,m为55kg,人体重心高度与栏杆最小距离h1取0.23m,人体的重心高度h0取1.05m,栏架高度h取1.067m,g取9.8/m/s2,后蹬作用时间t取0.30s。
当已知S0,如何控制θ,达到最佳起跳状态。
依据公式(5)得到如下数据:
当S0分别为1.35m、1.40m、1.45m、1.50m、1.55m、1.60m时,
对应θ,分别为76.6°、73.6°、70.5°、67.3°、64.1°、60.8°。
通过对以上数据进行分析可得,随着S0增大,θ不断减小。
2. 通过改变S0,得出S0与时间t的关系
假设到达起跨点的瞬时水平速度V0=5.0m/s,后蹬反作用力f为800N,质量m为55kg,人体重心高度与栏杆顶最小距离h1取0.23m,人体的重心高度h0取1.05m,栏架高度h取1.067m,重力加速度g取9.8m/s2,起跨角θ取700。
当已知S0,如何控制t后,达到最佳起跳状态。
依据公式(5)得到如下数据:
当S0分别为1.35m、1.40m、1.45m、1.50m、1.55m、1.60m时,
t分别为0.20s、0.25s、0.29s、0.34s、0.38s、0.43s。
随着S0增大,t不断增大。
(二)考虑空气阻力影响的情况下
假设空气的阻力在竖直方向上忽略不计,空气密度不变、运动员的人体直立时的正面面积近似于运动时的正面面积,此时空气阻力大小为:
由力f,空气的阻力′,起跨角θ,可以得到力f在水平方向上的分力大小为f*cosθ,水平方向上的合力Fx大小为:
Fx=f*cosθ-F′(7)
由公式(2)、(4)、(6)、(7)可知,跨栏时的起跨距离为:
1. 通过改变S0,得出S0与θ的关系
假设到达起跨点的瞬时水平速度V0=5.0m/s,后蹬反作用力f取800N,质量m为55kg,人体重心高度与栏杆顶最小距离h1取0.23m,人体的重心高度h0取1.05m,栏架高度h取1.067m,后蹬作用时间t取0.30s,重力加速度g取9.8m/s2,空气密度ρ取1/29kg/m3,空气阻力系数c取1.0,人体直立时的正面面积A0取1.0m2。
当已知S0,如何控制θ,达到最佳起跳状态。
可依据公式(8)得到如下数据:
当S0分别为1.35m、1.40m、1.45m、1.50m、1.55m、1.60m时,
θ分別为75.4°、72.3°、69.2°、66.1°、62.8°、59.5°。
随着S0增大,θ不断减小。
2. 通过不断改变,得出与时间的关系
假设运动员到达起跨点的瞬时水平速度V0=5.0m/s,力f大小800N,质量m为55kg,人体重心高度与栏杆顶最小距离h1取0.23m,人体高度取1.05m,栏杆高度h取1.067m,起跨角θ取70°,重力加速度g取9.8m/s2,空气密度ρ取1.29kg/m3,空气阻力系数c取1.0,人体直立时的正面面积A0取1.0m2。
当已知S0,如何控制时间t,达到最佳起跳状态。
依据公式(8)得到如下数据:
当S0分别为1.35m、1.40m、1.45m、1.50m、1.55m、1.60m时,
t分别为0.22s、0.26s、0.31s、0.36s、0.40s、0.45s。
随着S0增大,时间t不断增大。
(三)研究最优起跨角θ0的取值
1. 假设不考虑空气阻力的影响,后蹬反作用力f是已知的,设f=1000N,研究θ0的取值,变量有V0,S0,t
由公式(1)、(2)、(4)、(5),可知起跨角的最佳取值为:
存在θ0=θ(V0,S0,t)。
2. 假设不考虑自然风的影响,空气阻力F′,后蹬反作用力f是已知的,假设f=1000N,研究θ0的取值,变量有V0,S0,t
由公式(2)、(4)、(6)、(7)、(8)可知,起跨角的最佳取值为:
存在θ0=(V0,S0,t)。
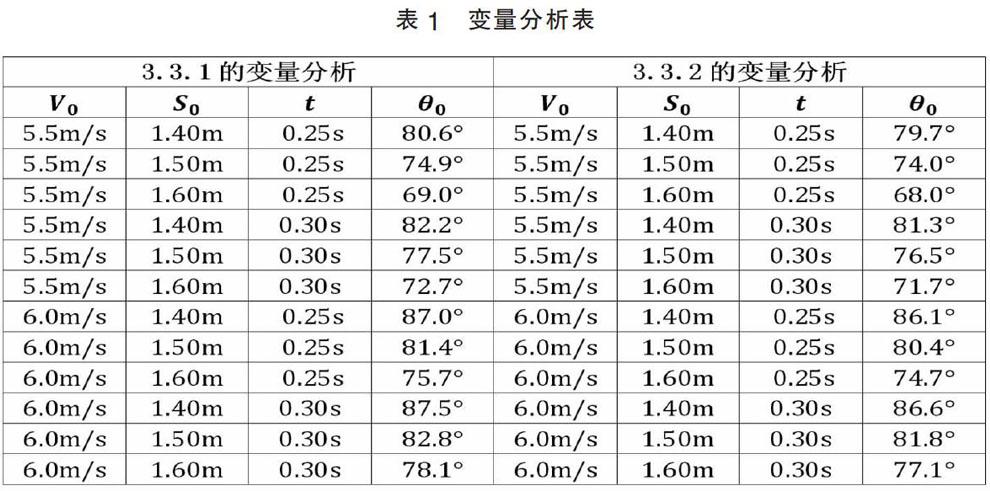
分析表1数据,可得到θ0与其他变量之间的关系为:
(1)在其他参数不变时,随着V0的增大,θ0逐渐增大;
(2)在其他参数不变时,随着S0的增大,θ0逐渐减小;
(3)在其他参数不变时,随着t的增大,θ0逐渐增大;
(4)在相同参数下,由于存在空气阻力,需要将水平方向上的分力略微增大,此时选择的θ0比不考虑空气阻力时略微减小。
四、总结
通过建立简单的数学模型并逐步进行分析,提出的问题基本得到解决,具有一定的实用性。而且通过研究跨栏的数学模型不仅可以提高学习数学的趣味性,还能加深对高中数学与物理中有关运动问题的理解。根据跨栏的实际情况(如:后蹬反作用力、后蹬作用时间、起跨距离、人体重心位置等因素)来确定起跨角。在跨栏的过程中,自然风对于运动员跨栏的影响,在本文中没有深入讨论,是此数学模型的局限之一。另外,此数学模型理念也可以运用于机器人对于角度和距离的选择问题上。希望此文对跨栏运动员能有所帮助。

