干涉光谱仪中动镜的磁悬浮支撑磁力解耦方法研究*

丁 超 许孟杰

（1.中国船舶重工集团公司第七〇九研究所 武汉 430205）（2.湖北科技职业学院 武汉 430000）

1 引言

干涉光谱仪的定性与定量分析功能的实现依赖于光程差的改变，通过动镜的不断运动可以改变光程差［1]，它要求动镜在扫描过程中具有高精度的匀速性和在垂轴方向很小的摆动，这就对仪器的机械精度和系统稳定性提出了很高的要求。

干涉光谱仪中要求动镜在运动过程中能够稳定而匀速，然而在干涉光谱仪的设计中发现，系统动镜在传统的驱动方法下不可避免地存在着运动不平稳等问题［2]。近代高精度的机械加工，已能制作出保证干涉仪平稳运动的机械轴承［3]，Nicolet公司初期采用了悬挂扭转式无磨损机构，悬臂可绕轴摆动，动镜产生前后直线运动；Analect公司楔状分束器干涉仪，仅让纯KBr制成的楔状补偿片作前后微小移动，就能获得相干光，移动使用机械轴承；Perkin-Elmer公司研发了变角摆动干涉仪，它去掉了经典干涉仪中支撑在空气轴承上直线移动的动镜。上述的各类改良型干涉仪，虽然去掉了空气轴承，但仅能在低分辨率仪器中使用。对于动镜驱动系统通常有旋转电机机械传动，电控气动液压系统和电磁驱动系统，但机械元件易产生弹性变形、摩擦、反向间隙、非线性误差等缺陷而电控气动液压系统虽然振动和倾斜小，但速度慢，结构复杂，需要供气供液系统，不利于仪器的小型化和受环境影响大。综上，如何能够在减小动镜系统重力的前提下，保证动镜驱动系统体积小，控制简单，精度也高，是本次研究的重点。

针对这一现象，本文对干涉光谱仪的动镜驱动系统展开研究，设计了磁悬浮动镜支撑系统［4]，同时配合音圈电机对动镜实现较为稳定匀速的控制［5]，但由于悬浮磁力系统与驱动系统中的音圈电机磁场与动镜处于同一系统当中，故动镜受到的磁力存在耦合的情况，影响了动镜在水平方向以及竖直方向上的受力结果的求解，无法对动镜进行有效的控制。所以本文对耦合的磁力进行解耦，精确地求解动镜的受力情况，从使动镜在运动过程能够维持匀速状态。该方法的高精度、强实时性，满足了干涉光谱仪中干涉仪的动镜匀速性的要求。

2 动镜系统的结构及原理

2.1 动镜的磁悬浮支撑系统结构及原理

我们采用音圈电机作为动镜的驱动系统，磁悬浮装置作为动镜的支撑系统。其中磁悬浮装置由石墨套筒支撑，石墨玻璃轴承位于玻璃套筒内，由音圈电机驱动动镜在玻璃套筒内滑动，由于柔性石墨系用天然鳞状石墨经过特殊的化学处理、热处理加工而成，它所制成元件，不含任何粘结剂，保持天然石墨的原有特性，而且密封性能良好，能够减小元件之间的摩擦力［6]。

利用石墨的这些特性，我们设计了磁悬浮动镜结合石墨玻璃轴承的动镜支撑装置［7]，如图1所示。

图1 动镜驱动系统的受力分析

图1中音圈电机与动镜由石墨轴承联接，玻璃套筒支撑，石墨玻璃轴承位于玻璃套筒内，由音圈电正上方的铁磁材料导轨间的磁力，抵消动镜石墨装置的重力可以使石墨轴承对于玻璃套筒基本无压力。圆柱形小磁铁与铁磁性抗旋转导轨间的磁性作用保证动镜运动时不发生旋转，使其具有导向性。音圈电机驱动动镜在玻璃套筒内滑动时主要用于平衡电磁铁对小磁铁的在水平方向上的分力。具体的受力分析情况如下。

在图1中F4主要是由整个系统的重力产生，F1则是由上方的电磁铁对小磁铁产生电磁力的竖直分力，F3为动镜运动过程中所受摩擦阻力与电磁铁对小磁铁水平方向力的合力，F2为电机产生的驱动力。适当调整小磁铁的位置使石墨轴承和动镜装置在电磁铁的力的作用下处于悬浮状态，减小石墨轴承以及动镜在运动过程中的摩擦力，在计算过程中可以近似认为此时的F1全部由电磁铁对小磁铁在水平方向的作用力提供。此时系统满足的力平衡方程式为

在动镜开始运动之后，要使该装置始终处于匀速运动状态，则使音圈电机的驱动力与电磁铁对小磁铁的水平分力相等。此时系统满足的力平衡方程式为

在满足了上述的两个式子之后，该系统便可以在减小系统由于重力产生的摩擦力以及在水平方向做匀速直线运动。

2.2 动镜的驱动系统结构及原理

在该系统中我们采用的是动圈式直线电机驱动动镜的运动［9]，该音圈电机［10]的机构图如图2。

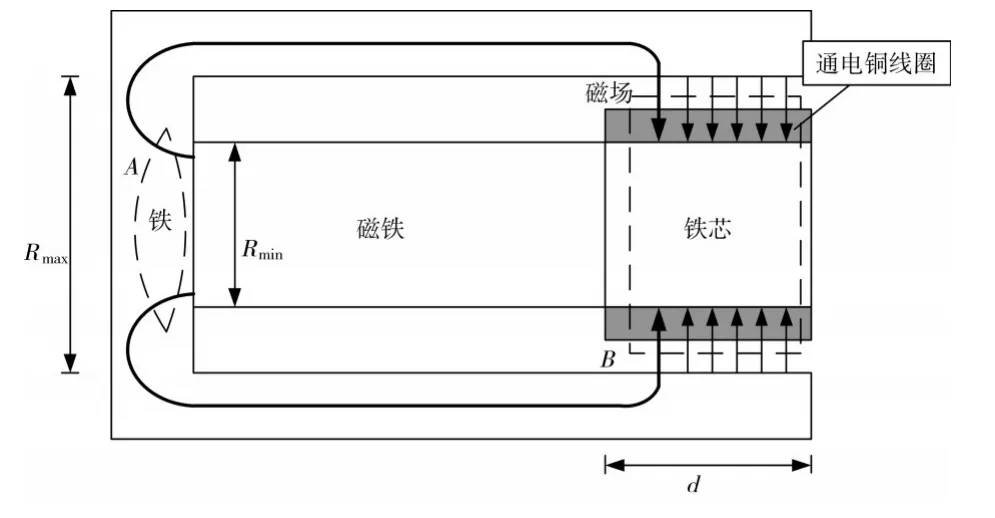
图2 音圈电机结构图

音圈电机在正常工作时，产生的电磁力大小可由式（3）进行计算：

式中：N为线圈匝数；L为线圈导体每匝处在磁场中的平均有效长度，单位为m；B为线圈所在空间的磁感应强度，单位为T；I为线圈导体中的电流，单位为A。

只要线圈受到的电磁力大于线圈支架上存在的静摩擦阻力Fs，就可使线圈产生直线运动。这就是音圈电机的基本原理。

由于音圈电机特殊的设计结构，使得运动线圈所处的磁场可以看作是均匀的，又由于线圈支架上的摩擦力很小，故可认为Fs=0［11]。

根据等效磁路模型可以认为从磁铁表面产生的磁通量与通过线圈所处气隙处的平面上所有的磁通量相等［12]。即通过图上虚线围成的面A与面B的磁通量大小相等，可以得到式（4）、（5）、（6）：

故将实际数据代入式（4）、（5）、（6），便可通过计算得到线圈所受的磁力大小。

3 磁悬浮支撑中的耦合问题及解耦方法

在本文所设计的动镜系统中包括了水平方向的驱动系统和在竖直方向的磁悬浮系统，而与动镜连接的小磁体处于这两个系统的力场中，故小磁体受到的力在两个力场的作用下会互相影响，存在耦合问题，导致无法通过对两个系统的分别控制来完成对动镜的平稳控制。

所以我们从整个系统的要达到的运动效果来分析，与动镜固定在一起的小磁体在竖直方向受到电磁铁的磁力用以始终平衡小磁铁的重力，但由于电磁铁固定在小磁铁的左上角所以随着小磁体在水平方向上的运动使得其在水平方向受到的分力始终不断变化，这就要求控制小磁铁水平运动的音圈电机始终产生一个用以平衡该分力的变化驱动力。如何求解音圈电机的电流大小，使动镜在竖直方向上不受力的情况下保持匀速运动，便是解耦的过程［13]，也是本文章着重解决的问题。

由于电磁铁周围的磁场分布较为复杂，并不能根据简单洛伦兹力的求解方法来计算电磁铁对小磁铁力的作用［14]，所以我们采用有限元分析的软件来计算电磁铁在小磁铁周围产生的磁场，并以此分析出小磁铁在运动方向上各个采样点的受力情况。在各个采样点通过对电磁铁通以不同大小的电流，然后将求得的小磁铁的受力情况进行整理、分析，我们可以模拟出小磁铁的位移，以及电磁铁通的电流大小与小磁铁在竖直方向和水平方向的受力大小的函数关系。

用F1表示电磁铁对小磁铁的作用力，可以很明显地知道F1是与电磁铁所通电流大小I1，小磁铁所在位置X有关。故电磁铁对小磁铁在水平方向上的施力情况为αF1( )I1，X。

电磁铁对小磁铁在竖直方向上的施力情况为βF1( )

I1，X。

由于音圈电机的线圈同样受到电机内部的磁场作用进行运动，因直接利用磁路定理对线圈的受力情况进行分析［15]。

用F2表示音圈电机对小磁铁的作用力，同样F2与控制音圈电机的电流大小I2。

F2()

I2表示音圈电机电机对小磁铁的施力大小。

G表示装置的重力。

故以上求解音圈电机电流I2的过程，即解耦过程可以用公式具体表示为

根据此式以及软件得到的函数关系便可以对应得到电磁铁的电流大小I1。然后便可以知道电磁铁对小磁铁水平方向上作用力的大小αF1( )I1，X，又因为

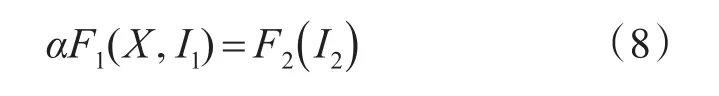
故根据此式以及模拟得到函数关系表的对应可以得到音圈电机的电流大小，完成解耦过程。

4 实验结果与分析

首先在ANSYS Maxwell建立了电磁铁与小磁铁的模型［16]，考虑到光谱仪的实际情况将小磁铁的运动行程设定为6mm，位置的采样设定为为每隔0.5mm进行一次测量；由于要求控制的精准性，所以将电磁铁线圈通过的电流范围设置为0～1A，且每隔10mA进行一次测量。这样电磁铁与小磁铁模型共具有1313个数据点。将这些数据点利用Matlab的sftool工具进行曲面拟合可以得到小磁铁受力的大小与小磁铁位置以及电磁铁电流的关系，并可以此确定函数F1( )I1，X。

由此得到的函数关系为

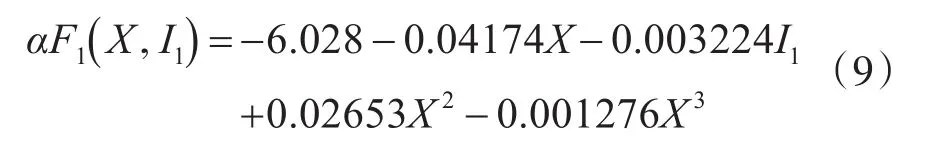
在水平方向上，通过对数据的分析由于在x≤2时小磁铁受力较小，故在拟合时将x=2作为分界点对该位置左右两边进行分别拟合。

当x≤2时，利用Matlab对测得的数据进行拟合得到的函数关系为

当2＜x≤6时，得到的拟合图函数关系为

对于音圈电机中线圈的受力模型，由于音圈电机中的磁场分布均匀，便可以根据磁路定理准确计算出线圈所处的磁场大小B，然后通过安培力的计算公式求得线圈的受力大小。

具体的计算过程：将音圈电机的具体参数N=100、Rmin=10mm、Rmax=13mm、d=10mm、B0=0.816T 带入到计算式（4）、（5）、（6）中得到B=0.355T。

故音圈电机中的线圈受力大小为

根据上述的解耦方法以及拟合得到的函数关系便可以求解出控制音圈电机的电流大小I2。下面将对拟合得到的函数关系进行验证。

对于小磁铁与电磁铁模型，将大量数据点带入到已得到的拟合函数中，可以得到根据已知点的位置以及电流大小确定的小磁铁所受电磁力的大小：

当位置X=0.7mm，1.4mm，2.1mm，2.8mm时，且电流从0mA～1000mA变化时。

通过拟合函数计算得到小磁铁在竖直方所受电磁力大小和水平方向所受电磁力大小，然后分别与在ANSYS Maxwell软件中建立模型仿真得到的力的大小进行比较，得到的误差结果如表1所示。

表1 小磁铁的受力拟合误差

通过以上的对比验证可以看出模拟值与真实值之间的误差较小，可以满足电磁铁对小磁铁的控制要求。说明通过有限元软件Maxwell仿真得到的拟合关系能够有效地表示出电磁铁与小磁铁模型在位置与电流大小变化的情况。因此可以依据得到的函数式准确进行解耦过程的第一步，即通过已知的位置及小磁铁的重力便可以准确得到电磁铁通的电流大小。

对于音圈电机模型直接计算出音圈电机中的磁场大小，故可以依据求解安倍力的公式直接得到的电流I2与线圈受力大小的关系，进行求解完成解耦的第二步。

我们将对动镜的控制电流进行解耦验证。

设动镜的重力大小为7.50N，动镜所处的位置X=1.4mm。通过拟合函数求解：

依据式（7）以及式（9）可以解得对应的I1=453.51mA；

当I1=453.51mA时，由式（10）得小磁铁水平受力大小F1=451.19mN；当F1=451.19mN时，由式（12）得到I2=0.202A。

此时将得到的I1，I2以及X=1.4带入到建立的模型当中，可以得到电磁铁对小磁铁竖直方向的作用力F3=7.44N，水平方向上的作用力F2=546.45mN。

因此可以得出结论，在竖直方向上与系统重力的误差为0.06N，能够有效减小动镜系统的重力；在水平方向上的误差为0.095N，可以认为动镜系统在水平方向上所受合力为0，故动镜在水平方向上做匀速运动。

同 样 的 选 取X=0.7mm，1.4mm，2.1mm，2.8mm处的位置进行解耦验证，解耦方法与X=1.4mm处的解耦方法相同，得到的结果如表2所示。

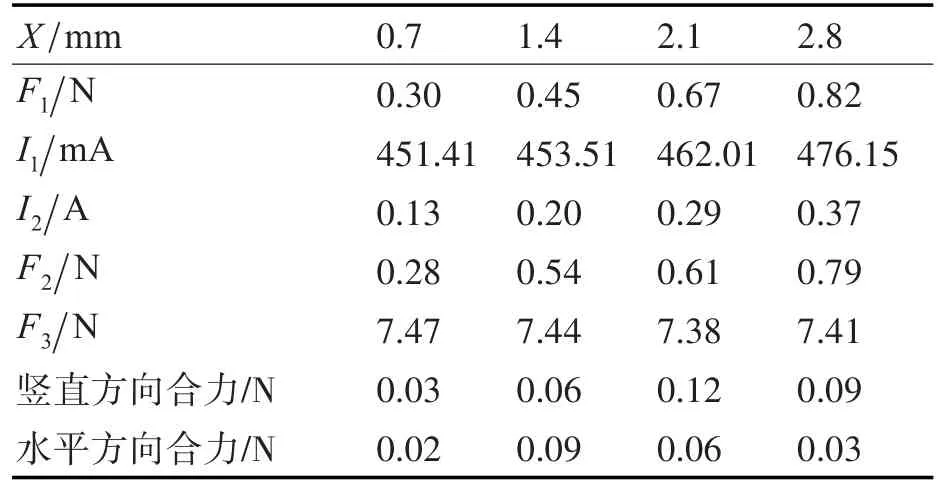
表2 解耦电流控制下的动镜受力情况

通过验证可以知道在解耦得到的电流控制下动镜在水平方向上和竖直方向上的合力在误差允许范围内可以看作为0，说明磁悬浮支撑装置能够有效地抵消动镜系统的重力，且音圈电机构成的动力系统能够在动镜运动过程中使其保持匀速运动。

5 结语

通过有限元软件ANSYS Maxwell对动镜的控制部分分别进行了建模并得到了较好的模拟效果。根据对不同部分的建模分析得到了小磁铁以及线圈在各自磁场中的受力关系，且通过大量的数据验证了函数关系的可靠性。借此函数关系我们便能够轻松地对控制电流进行解耦，得到控制音圈电机的电流，通过验证解耦得到的电流在竖直方向上能够有效抵消动镜装置的重力，在水平方向上音圈电机对动镜的作用力能够有效平衡电磁铁对动镜装置的水平分力，所以解耦得到的电流能够精确的控制动镜的运动，使其始终能够保持匀速平稳的运动，从而增加干涉仪的稳定性与精度。