基于改进LDPC矩阵的遥感图像重构算法研究*

许晓明

（南京理工大学 南京 210094）

1 引言

当前，在遥感数据的发现方面体现出两个主流的趋势：一是遥感数据发展对高数据率的需求；二是遥感探测范围不断扩大。而随着当前传感器的多样化，以及遥感数据量的增加，要获取更为准确的遥感图像，必须要提高和改善遥感图像采集系统的性能。但当前的遥感图像采集大部分是采用Shannon-Nyquist采样技术。这种采样技术要求采样的频率需要达到信号频谱最高频率的两倍以上，这样才能保证重构信号不失真。这种采样存在一定的缺陷，如采样受到速率的限制，二是压缩编码需要舍弃大量的冗余数据，由此造成遥感图像资源的浪费［1～5]。对此，为解决这个问题，人们提出将压缩感知技术应用到遥感图像的处理中，以提高图像传输的速率。而研究认为，压缩感知过程中，信号的重构是线性规划问题。由于压缩采样，使得采样数远小于原始信号的长度，由此使得该线性规划问题为一个方程数少于未知数，从而使其存在无数个解。为解决这个问题，人们提出采用观测矩阵进行求解。周春佳、孙权森等研究发现，采用传统的观测矩阵，如高斯矩阵会增加压缩感知的时间，同时由于观测矩阵中的元素是浮点数，所以在存储方面也存在一定的限制。并且由于计算量大，给硬件实现带来极大的挑战。另外，观测矩阵的维数较高，实际传输中会有很大损耗。传统的高斯随机矩阵、随机稀疏矩阵等的构造都不简单，即在矩阵高度稀疏且元素二值化方面较为复杂。因此，结合遥感图像采集处理的需求，本文提出一种LDPC的观测矩阵方法。

2 LDPC观测矩阵构造

2.1 LDPC编码

LDPC码为一种具有系数校验矩阵的线性分组纠错码，也可用零空间的稀疏矩阵形式表示。在校验矩阵中，通常只有少数的元素用“1”表示，其中大部分的元素是用“0”表示的一个稀疏矩阵。而LDPC码自身的低密度，也源于校验矩阵自身的稀疏性。在LDPC码中，可以分为两类［6]：一类是不规则的LDPC码，其校验矩阵中的各行和各列的零元素个数不同；另外的一类则是规则的LDPC码，即在各列和各行中，零元素的个数相同。式（1）为一种规则的LDPC码所构造的校验矩阵（10，2，4）。

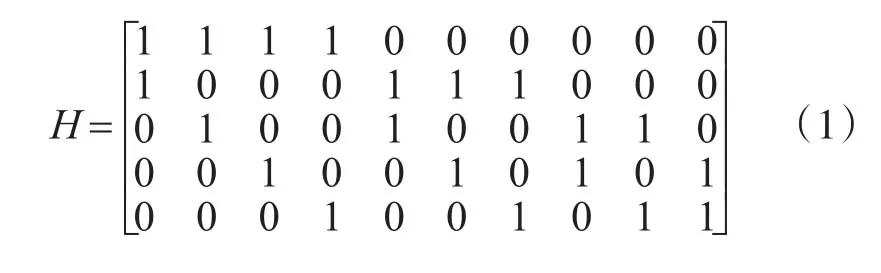
2.2 LDPC校验矩阵构造

通过式（1）看出，通过LDPC构建的校验矩阵是一个由“0”和“1”组成的一个稀疏二值矩阵。在该矩阵中，各列之间尽可能的线性无关，因此在压缩感知的过程中可以作为观测矩阵来应用。而在观测矩阵的构造过程中，要求尽可能避免出现长度为4的短环。另外，环长度越长，构造的校验矩阵则性能越好［7]。为构建校验矩阵，仁恩提出了随机构造法和结构化构造法。在本文中，则采用随机构造法中的Mackay法对校验矩阵进行构建［8]。以列重3，码率为1/2为例，其具体的构造如图1所示。

图1 Mackay1A构造法示意图

根据图1的构造可以看出，采用y1A构造法后，得到的矩阵行重为6。

2.3 LDPC观测矩阵的构造

结合上述理论的启发，本文希望借助LDPC校验矩阵构建一个简单且效果优的观测矩阵。对此，采用Mackay 1A构造法中的左半边利用Gallager构造法，从而将两者全部级联在一个矩阵当中。具体构造步骤为

输入：矩阵行数、列数、列重、行重，即M、N、γ和、ρ

1）构造子矩阵H1，设定其行数和列数分别为：M／γ、N-M；H1的第i行的“1”直接从 ( )i-1K+1开始到第iK开始排列，其中的K=r×M／N；

2）将子矩阵H1中的各列顺序进行随机置换，进而生成（γ一1）个新的子矩阵，用Hi表示，

3）将γ个子矩阵按照矩阵列的方向，合成一个新的大小的矩阵，用Φ1表示；

4）构造大小为M×M的随机二值矩阵Φ2，使其列重大小为γ，其行重尽可能的相等；

5）将矩阵Φ1和矩阵Φ2进行级联，继而得到M×N的校验矩阵Φ。

通过上述的构造，充分结合了传统的Mackay矩阵和Gallager矩阵构造的优点，提高了重构时间。

3 LDPC观测矩阵改进

在对上述的构建工程中，我们发现LDPC编码构造的观测矩阵，与传统的随机稀疏二值观测矩阵相比，在计算的复杂度上都没有明显的优势。因此，要减少计算的复杂度，简化观测矩阵的构造，尝试结合对角块矩阵。对角块矩阵与其他观测矩阵相比，存在明显的优势，就是只需在对角线的位置放置少量的矩阵快［9]。由此，这样可以极大地减少图像重构过程中的计算量，提高计算的速度。同时，为提高后期图像采集过程中硬件的实现效果，去掉随机置换过程。具体构造为假设传统置乱对角块矩阵存在L个的对角块矩阵，用A0=diag(a1，a2， ...，ak1) ，B0=diag(b1，b2， ...，bk1) ，…由此，通过L种不同的置乱方式，可以生成观测矩阵Φ。在该观测矩阵中，LDPC矩阵块为该矩阵的一个子矩阵，并且其每个对角线的位置的子矩阵都是相同的。具体如图2所示。

由此，通过这种方式大大减低了构造的难度，也提高了计算的效率。而在图2中也可以看出，其中的每个LDPC对角块是相互独立的，且LDPC块的个数为k=N/M。

4 仿真实验对比

4.1 图像质量评价指标

为验证对角块观测矩阵与其他观测矩阵的优势，本文参考相关的文献，以PSNR和SSIM作为主要的参考指标。

4.1.1 峰值信噪比（PSNR）

PSNR为一种用于图像质量评价的客观测量方法，其主要是通过对原图像和经过处理后图像的均方差相对于（2n-1）2的对数值，以此来衡量经过处理后的图像的质量。该值越大，说明原始图和经处理后的图之间越相似。

4.1.2 结构相似度（SSIM）

研究认为自然图像本身是高度结构化的，并且其像素之间存在很强的依赖性，并且在图像中包含了大量的视觉景象信息。因此，人们提出基于图像结构的相似度。其具体的计算为

其中，SSIM∈（0，1），取值越大，说明相似度越高，重构效果越好。

4.2 实验方案

为验证上述的改进效果，采用了两组实验对图像效果进行评比。

实验1：

选择经典灰度测试图像Lena进行重构，图像分辨率为512×512像素。在对图像进行重构过程中，首先对图像进行分块，然后通过不同的观测矩阵对图像进行采样，最后对图像进行重构。图像分块采用DCT字典，图像重构方法采用OMP算法。同时每种方法测试200次，然后比较每种方法的PSNR和SSIM值。

同时，用16×64的观测矩阵对Lena测试图像进行重构，从而得到如图3的重构结果。

通过图3看出，采用LDPC对角块矩阵得到的图像重构效果要明显好于采用其他观测矩阵得到的图像［10]。而为了更好地更为客观地分析重构质量，通过实验得到PSNR和SSIM指标。具体见图4。

图3 不同观测矩阵对Lena的重构结果

图4 不同观测矩阵重构Lena图像的评价指标

实验2：

对图5的512×512的某遥感图像进行重构，稀疏基同样采用8×8原子大小的DCT字典，重构算法采用 OMP［11～12]，观测矩阵采用 16×64 大小。通过重构得到图6的遥感图像。

图5 山脉遥感图像

通过重构，得到图6的重构结果。对图像6的重构看出，采用对角化的观测矩阵得到的重构图像较清晰。同样通过多次试验对PSNR和SSIM的统计，得到表1的结果。

图6 重构结果

表1 四种不同观测矩阵重构的评价结果

综合比较，对角化LDPC观测矩阵的重构效果优于其他同等规模的观测矩阵重构效果。

5 结语

通过上述的研究看出，LDPC校验码在图像重构方案具有较强的优势，借助其优势取代了传统置乱对角块矩阵当中的对角块，并简化了观测矩阵。同时，通过仿真也验证了采用LDPC校验码对对角块矩阵的构建具有很强的优势，在相同规模的观测矩阵下，对角块化后的LDPC观测矩阵得到的重构遥感图像更清晰。