导数测试题B卷

■河南省太康县第一高级中学

一、选择题

1.曲线y=xex-1在点(1,1)处的切线的斜率等于( )。

A.2 e B.e C.2 D.1

2.已知函数f(x)=2 ln3x+8x,则的值为( )。

A.1 0 B.-1 0 C.-2 0 D.2 0

4.已知a,b为正实数,直线y=x-a+2与曲线y=ex+b-1相切,则的最小值为( )。

A.1 B.2 C.4 D.8

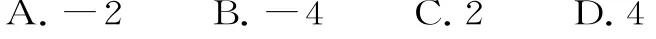
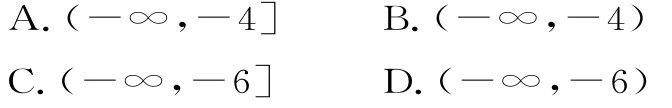
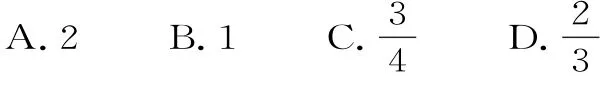
8.已知函数y=f(x)的图像如图1所示,则它的导函数y=f'(x)的图像可以是图2中的( )。

图1

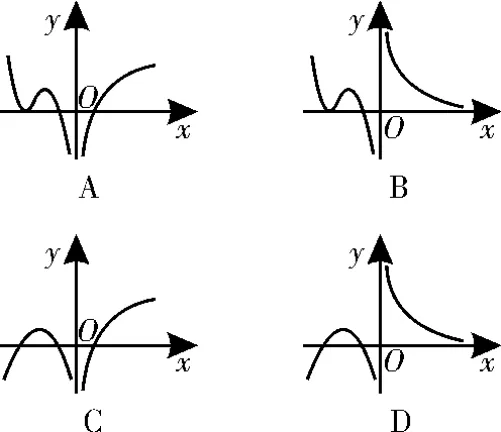
图2

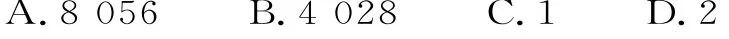
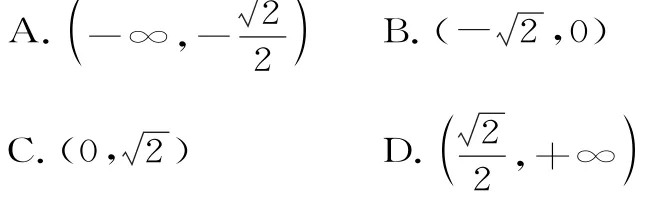
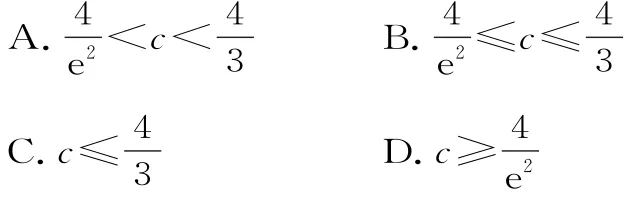
12.函数f(x)是定义在(1,+∞)上的可导函数,f'(x)为其导函数,若f(x)+(x-1)f'(x)=x2(x-2),且f(e2)=0,则不等式f(ex)＜0的解集为( )。

二、填空题

13.若函数f(x)=ln(x+2)的图像在点P(x0,y0)处的切线l与函数g(x)=ex的图像也相切,则满足条件的切点P的个数为____。

三、解答题

17.一质点运动的方程为s=8-3t2。

(1)求质点在[1,1+Δt]这段时间内的平均速度;

(2)求质点在t=1时的瞬时速度(用定义及求导两种方法)。

(1)求f(x)的最小值;

(1)讨论函数f(x)的单调性;

(2)求证:当a≥3-e时,对于任意的x∈[0,+∞),有f(x)≥-1恒成立。

(1)求曲线y=f(x)的斜率为1的切线方程。

(2)当x∈[-2,4]时,求证:x-6≤f(x)≤x。

(3)设F(x)=|f(x)-(x+a)|(a∈R),记F(x)在区间[-2,4]上的最大值为M(a)。当M(a)最小时,求a的值。