微积分易错题归类剖析
■河南省太康县第一高级中学
本文通过对几个易错题型的分析,强调说明在利用微积分基本定理求定积分的问题上应注意的事项,以及运用牛顿—莱布尼茨公式和做变换时应注意哪些问题。
在一元函数的微积分学中,微积分基本定理是一个非常重要的定理,一般地,如果f(x)是区间[a,b]上的连续函数,并且F(a)这个结论叫作微积分基本定理,又叫作牛顿—莱布尼茨公式。它的主要意义在于描述了定积分与原函数即不定积分之间的联系,给出了计算定积分的一种统一的、简便的方法,极大地简化了定积分的计算过程。
微积分基本定理指出了求连续函数定积分的一般方法,把定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁,揭示了导数和定积分的内在联系,同时也提供计算定积分的一种有效方法。
教材中微积分的课时少,同学们学习时如果对其重视不够,对微积分基本定理及其运用的理解不够透彻,对微积分定理的应用不够熟练,对公式的记忆不准确、不熟练,就会导致在解题中出现一些错误。下面通过具体例题,对微积分中的易错题型作些分析。
易错题型一:忽视公式成立的条件
例1 求
错解:
错因分析:本题解法的错因是忽略了牛顿—莱布尼茨公式成立的条件,因为在区间[- 1,1]上,函数在点x=0处没有定义,不满足可积条件,因此不能使用牛顿—莱布尼茨公式。
正解:
例2 求
错解:因为为奇函数,积分区间(-∞,+∞)是关于原点对称的区间,所以
错因分析:这里的积分区间(-∞,+∞)是关于原点对称的区间,积分区间是无穷区间,它的性质与定积分不同,做法不能按照微积分基本定理和定积分的性质来进行做题。
正解:,因 为,所以是发散的。
点评:很多学生把公式、法则都记住了,错题集也看了,但是往往做题时还是会出错,且不知道自己错在哪了,为什么错,所以仅仅死记公式、法则是不行的,错解中忽略了公式、法则的意义和成立的条件。
易错题型二:忽视被积函数的化简
例3 求
错解:
错因分析:其一是绝对值在没有去掉的前提下就开始求解,其二是三角函数的导数公式记得不准确;使用微积分基本定理需要注意:(1)对于含有绝对值符号的被积函数,要根据定义域先去掉绝对值再求积分;(2)对被积函数要先化简,再求积分;(3)当被积函数是分段函数时,利用定积分的性质先分段,转化为各区间上定积分的和。
正解:
易错题型三:对于原函数的理解不清晰
例4 定义在R上的函数f(x)过点(0,2),且f'(x)=4x,求
错解:因为f'(x)=4x,所以f(x)=2x2,所以
错因分析:对原函数的理解不透彻,误认为f(x)=2x2,在运用微积分基本定理求解定积分时经常会把原函数的常数项忽略掉,从而错误地认为一个函数的原函数只有一个,实际上,一个函数的原函数有无数多个。
正解:因为f'(x)=4x,所以f(x)=2x2+c。
因为函数f(x)过点(0,2),则f(0)=2·02+c=2,c=2,所以f(x)=2x2+2。
易错题型四:利用微积分计算含有参数的定积分问题时易混淆概念
例5 已知,求函数F(a)的最小值。
错解
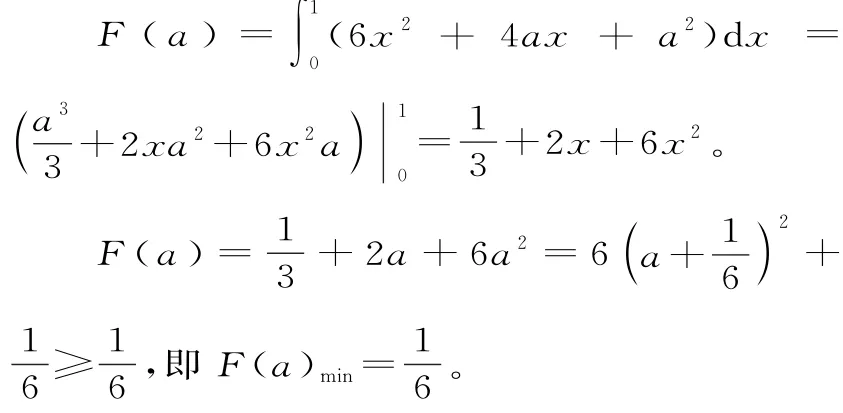
错因分析:积分变量与被积函数f(x)、积分上限与积分下限、积分区间与函数F(x)这些概念混淆一起,弄不清楚谁是被积函数,谁是积分变量。
正解:
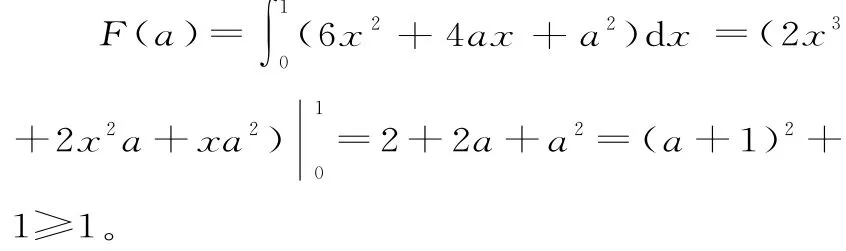
所以F(a)min=1。
点评:含有参数的定积分问题应注意以下两点:(1)含有参数的定积分可以与方程、函数或不等式综合起来考查,利用微积分基本定理计算定积分是解决此类问题的前提;(2)计算含有参数的定积分,必须分清积分变量与被积函数f(x)、积分上限与积分下限、积分区间与函数F(x)等概念。
跟踪练习:
1.若f(x)在R上可导,f(x)=x2+2f'(2)x+3,求
答案:1.-1 8