基于迈克耳孙干涉仪与线阵CCD的金属丝杨氏模量测量方案

姜 悦 吴官东

(金陵科技学院理学院，江苏 南京 211169)

杨氏模量是描述固体材料抵抗弹性形变能力的重要力学参数，是工程设计中选择机械构件材料的重要依据之一，对它的精确测量在科学研究和技术应用中都具有重要意义。在工程技术和实验教学中测量金属材料的杨氏模量通常采用静态拉伸法，其关键在于测定金属受力伸长时的微小形变。目前测微小形变的常用方法有光杠杆法[1,2]、电桥法[3]、光电传感器法[4]、莫尔条纹法[5,6]等，但普遍存在测量精度不高、调节与读数不方便等问题。本文设计了一种基于迈克耳孙干涉仪的金属丝杨氏模量测量新方案，并用线阵CCD结合单片机编程实现对干涉条纹移动的自动计数，使测量过程更方便、测量结果更精确。

1 测量原理

一根粗细均匀的圆柱形金属丝，初始长度为L，直径为d。给金属丝施加沿长度方向的外力F时，在弹性限度内金属丝的伸长量为ΔL。由胡克定律可知其杨氏模量为[2]

(1)

其中的ΔL是测量杨氏模量中最关键的待测量，也是最影响测量精度的物理量。本方案利用迈克耳孙干涉仪测量金属丝的伸长量ΔL，可实现在激光波长量级(即几百纳米)上的微小伸长量的精确测量。

1.1 迈克耳孙干涉仪测镜面M1位移量

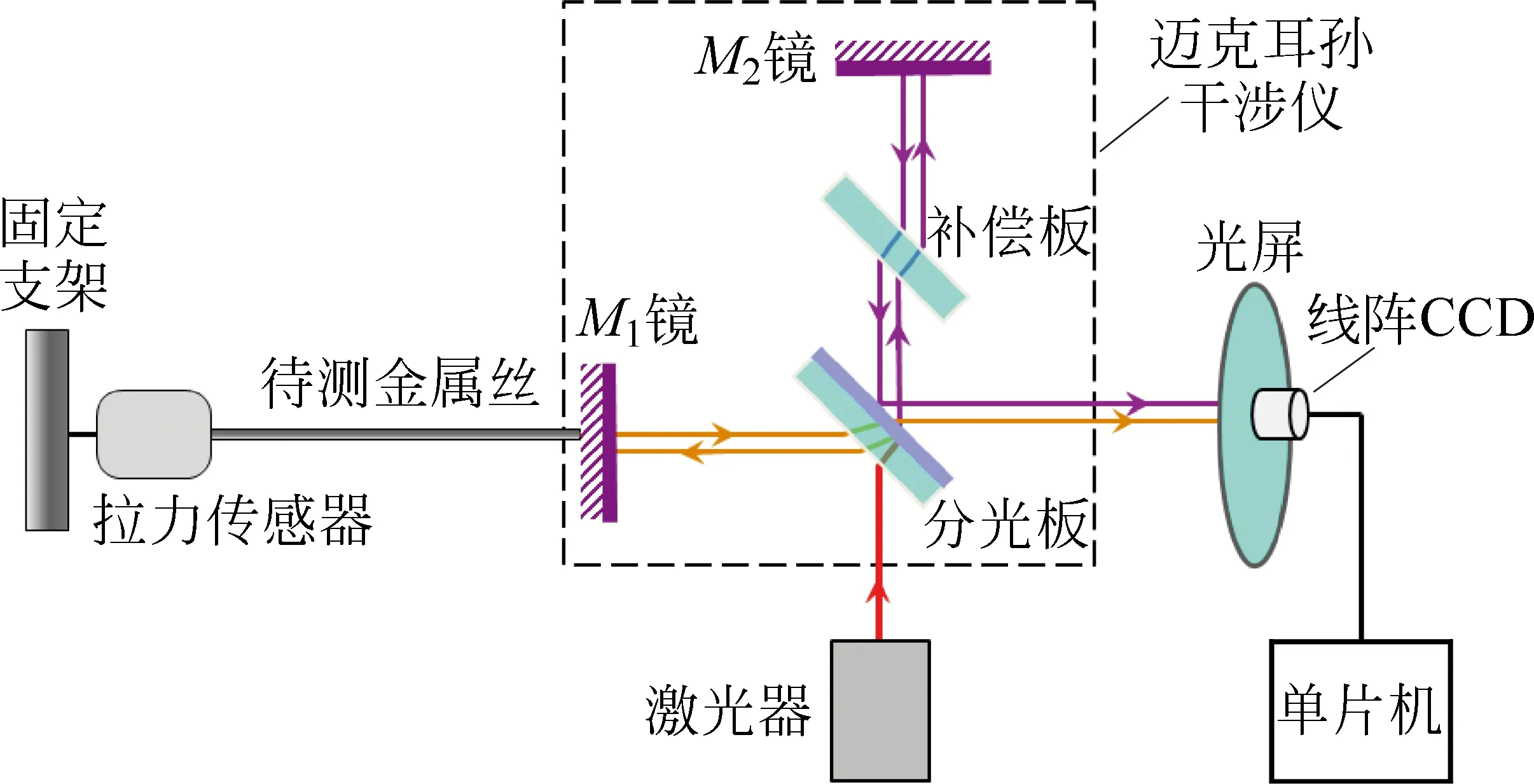
图1 实验装置示意图

如图1所示，待测金属丝与拉力传感器相连接，左端固定在支架上，金属丝右端固定在迈克耳孙干涉仪的移动反射镜M1的底座上。激光器发出的光被45°放置的分光板分成相互垂直的两束相干光，分别由竖直的M1镜、水平的M2镜反射后再经由分光板到达右边的光屏上，屏上将出现干涉圆条纹。缓慢转动迈克耳孙干涉仪的微调手轮，使M1镜的位置发生移动，金属丝中的拉力和金属丝的形变均会发生变化，此时光屏上的干涉圆环会出现吞吐现象。M1镜的位置每改变半个波长，干涉圆环中心冒出或缩进一环。读取条纹移动数目N，则M1镜位置的变化(与金属丝的位移相关)为

Δx=Nλ/2

(2)

式中λ为激光的波长。

1.2 线阵CCD自动记数

若人工读取干涉圆环移动数目，眼睛易疲劳，出错率也较高。针对此问题，将线阵CCD图像传感器安装在接收光屏中心处，捕获激光干涉的光强信号，通过模数转换后接入单片机，并使用C语言编写程序对干涉圆环移动自动计数。每当干涉圆环中心处的光强由最大阈值变化为最小阈值(或由最小阈值变化为最大阈值)时，圆环移动数目加记0.5个，程序流程图如图2所示。

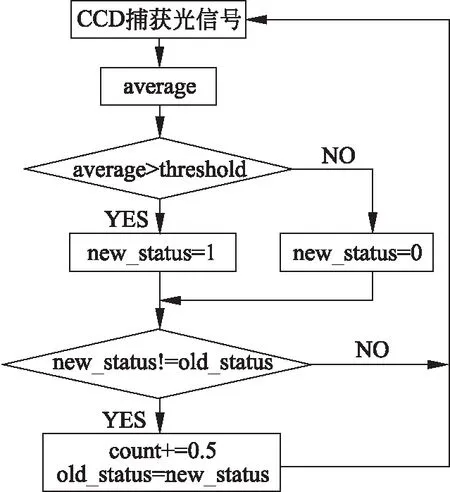
图2 计数程序流程图

1.3 拉力传感器自身形变的测量

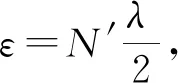
1.4 金属丝的形变伸长量

由上测量可知，用M1镜的总位移减去拉力传感器自身的形变，即可得到金属丝的形变伸长，即ΔL=Δx-ε。

综上，测量金属丝直径d和原长L，再将金属丝所受的拉力F和伸长量ΔL一起代入式(1)，即可计算杨氏模量E。

2 实验装置

实验装置照片如图3所示，使用氦氖激光器作为光源。为方便固定金属丝和接收光屏，对现有的迈克耳孙干涉仪进行了改造。用一根长直金属棒穿过干涉仪底座的中心，待测金属丝与S型

表1 拉力传感器形变的测量数据

图3 实验装置实物照片

拉力传感器连接，一端固定在金属棒左侧安装的竖支架上，另一端与干涉仪上的M1镜相连，金属丝中的拉力值可由与拉力传感器相连的应变仪显示屏幕上读取。金属棒右侧安装接收光屏，线阵CCD与STM32F103单片机连好线(如图4)后，将CCD粘贴在光屏的中心(如图5)。

图4 STM32F103单片机连接线阵CCD

图5 中心处安装了线阵CCD的光屏

3 实验结果与分析

3.1 实验结果

实验使用的激光波长λ=632.8nm，用千分尺测得金属丝直径d=1.016mm，以金属丝中拉力F0=10.00N时作为初始状态，用米尺测得金属丝原长L=40.54cm；拉力每增加1.00N记录干涉圆环移动数目直至拉力增加10.00N，之后再每减小1.00N记录干涉圆环移动数目，得出各拉力对应的条纹平均移动数目N，并用逐差法计算金属丝的平均伸长量，数据见表2。

将各测量结果化为国际标准单位代入公式计算得

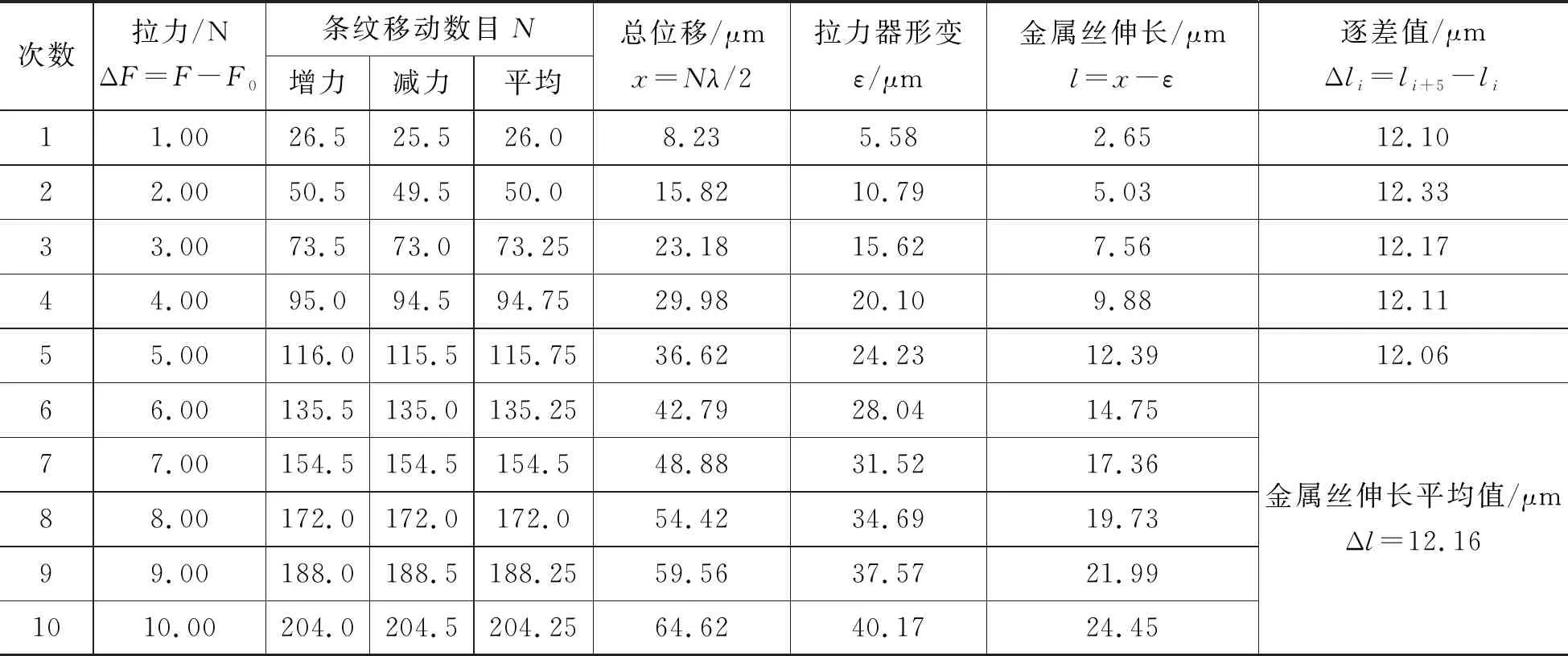
表2 金属丝形变伸长量的测量数据及计算

3.2 不确定度计算

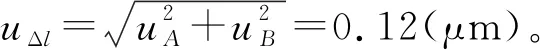
故杨氏模量的不确定度为uE=2.056×1011×1.3%(N·m-2)=0.027×1011(N·m-2)，置信概率p=0.95。

3.3 实验结果分析

综上所述，实验测得金属丝的杨氏模量为E=(2.056±0.027)×1011N·m-2，与金属丝生产厂家给出的数据2.05×1011N·m-2吻合较好。我们对同样的金属丝用传统光杠杆法测定了其拉伸形变，所得的杨氏模量是(2.02±0.09)×1011N·m-2。比较可知，本实验方法测量结果的准确度明显高于光杠杆法，不确定度也有显著的降低。

4 结论

本文设计了一种用迈克耳孙干涉仪测量金属丝杨氏模量的方法，仅需很小的拉力变化即可观察到明显的干涉条纹移动，可使待测金属丝长度大为缩短、仪器更加紧凑；用拉力传感器测定金属丝中的拉力，相比于通常物理实验中通过增减砝码改变拉力，可使拉力变化的间隔缩小且可调；用单片机编程控制CCD线阵实现干涉圆环移动的自动计数，操作更便捷，读数更准确。本测量方案对实验室现有装置迈克耳孙干涉仪进行改造，使用的中低端单片机STM32F103、蓝宙电子线性CCD传感器模块和S型拉力传感器都具有价格低、体积小的特点，实验方案总体成本低、操作容易、读数方便。实验测量结果显示，该方法能显著提高测量结果的精度，降低测量结果的不确定度。