费马原理在旋转二次曲面理想成像中的应用——主轴上物点

万建杰 赵鑫婷

(西北师范大学物理与电子工程学院，甘肃 兰州 730070)

费马原理即光沿光程为极值的路径传播，其数学公式为

(1)

笔者在文献[1]和文献[2]中给出了直接应用费马原理推导得到主轴外物点经过球面界面反射和折射的会聚光线方程和发散光线方程的一般过程。另外，文献[3]研究了旋转二次曲面的成像公式，具体推导了凸曲面折射的会聚光线方程及相应的物像公式，然而并未对会聚光线和发散光线作出区分。

本文将从新笛卡尔坐标系[4，5]出发，直接应用费马原理，讨论主轴上物点经旋转二次曲面反射和折射过程中产生的会聚光线和发散光线。

1 主轴上物点的旋转二次曲面反射

1.1 凹曲面反射的会聚光线

(2)

由于

(3)

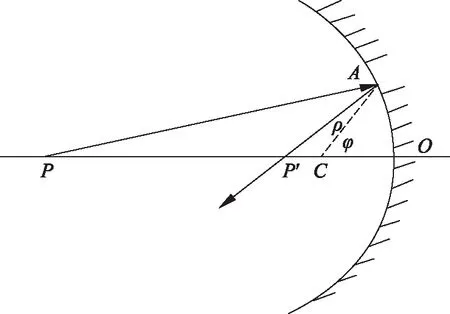
图1 主轴上物点的凹曲面反射

(4)

光程可以写成

(5)

先将式(5)对φ求导，即

(6)

(7)

根据费马原理，要使式(7)对任意φ都成立，只需

(8)

考虑到

即

(9)

或

(10)

此即主轴上物点凹曲面反射的会聚光线方程，该结果与文献[3]的式(17)略有不同。另外，当偏心率e=0时，凹曲面反射的会聚光线方程退化为凹球面反射的会聚光线方程[1, 4，5]。

1.2 凸曲面反射的发散光线

(11)

由于

(12)

图2 主轴上物点的凸曲面反射

(13)

则

(14)

先将式(14)对φ求导，即

(15)

(16)

根据费马原理，要使式(16)对于任意φ都成立，只需

(17)

或

(18)

此即主轴上物点经凸曲面反射的发散光线方程。可以看出，该方程与主轴上物点经凹曲面反射的会聚光线方程式(9)或式(10)不同。另外，当偏心率e=0时，凸曲面反射的发散光线方程退化为凸球面反射的发散光线方程[2]。

1.3 旋转二次曲面反射的理想成像

1) 凹曲面镜会聚光线的理想成像

在近轴光线条件下φ很小，因此

代入式(10)可得

(22)

即

(23)

上式即旋转二次曲面反射的实像物像公式。

2) 凸曲面镜发散光线的理想成像

在近轴光线条件下φ很小，因此

代入式(18)可得

(27)

即

(28)

上式即旋转二次曲面反射的虚像物像公式，在新笛卡尔坐标系中的物像公式(27)与实像物像公式(22)完全相同。可以看出，当偏心率e=0时，式(22)和式(27)即成为球面界面反射的物像公式[1，2,4，5]。当e=1时，可得出旋转抛物面反射的物像公式，焦点恰好是抛物面顶点O的曲率中心C。

2 主轴上物点的旋转二次曲面折射

2.1 凸曲面折射的会聚光线

(29)

图3 主轴上物点的凸曲面折射

由于

则

(32)

先将式(32)对φ求导，即

(33)

(34)

根据费马原理，要使式(34)对任意φ都成立，只需

(35)

或

(36)

此即主轴上物点凸曲面折射的会聚光线方程，与文献[3]的式(5)一致。当偏心率e=0时，凸曲面折射的会聚光线方程退化为凸球面折射的会聚光线方程[1, 4，5]。

2.2 凹曲面折射的发散光线

图4 主轴上物点的凹曲面折射

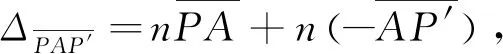
(37)

其中，p为半正焦弦。由于

光程可以写成

(40)

先将式(40)对φ求导，即

(41)

(42)

根据费马原理，要使式(42)对任意φ都成立，只需

(43)

即

(44)

或

(45)

此即主轴上物点经凹曲面折射的发散光线方程，可以看出，该方程与主轴上物点经凸曲面折射的会聚光线式(35)或式(36)明显不同。另外，当偏心率e=0时，凹曲面折射的发散光线方程退化为凹球面折射的发散光线方程[2]。

2.3 旋转二次曲面折射的理想成像

1) 凸曲面折射会聚光线的理想成像

在近轴光线条件下φ很小，因此

代入式(36)可得

(49)

即

(50)

上式即旋转二次曲面折射的实像物像公式。

2) 凹曲面折射发散光线的理想成像

在近轴光线条件下φ很小，因此

代入式(45)可得

(54)

即

(55)

上式即旋转二次曲面折射的虚像物像公式。可以看出，在新笛卡尔坐标系中，旋转二次曲面折射的实像和虚像物像公式具有相同的形式。另外，当偏心率e=0时，式(49)和式(54)退化为球面界面折射的物像公式[1-2,4-5]。

3 总结

本文运用费马原理直接推导得到了主轴上物点经旋转二次曲面反射和折射过程中产生的会聚光线和发散光线满足的几何关系，然后在近轴条件下得出旋转二次曲面的物像公式。结果表明凹曲面反射的会聚光线和凸曲面反射的发散光线满足不同的光线方程，凸曲面折射的会聚光线和凹曲面折射的发散光线也满足不同的光线方程。然而，在近轴条件下反射过程的(实像和虚像)物像公式和折射过程的(实像和虚像)物像公式在新笛卡尔坐标系中都分别具有统一的形式。特别地，当偏心率e=0时，旋转二次曲面退化为球面界面，相关方程也都退化为球面界面的光线方程和物像公式。

另外，根据文献[1,2,4,5]可以看出，当n′=-n时，凹球面折射发散光线方程变为凹球面反射会聚光线方程，而凸球面折射会聚光线方程变为凸球面反射发散光线方程，并且球面折射物像公式也会变成球面反射物像公式。同理，我们发现对于旋转二次曲面而言，当n′=-n时，凹曲面折射发散光线方程变为凹曲面反射会聚光线方程，而凸曲面折射会聚光线方程变为凸曲面反射发散光线方程，并且旋转二次曲面折射物像公式也变成相同曲面的反射物像公式。