粒子群算法和支持向量机的网络入侵检测
余森, 赵冉
(河南工业职业技术学院 1. 教务处; 2. 人事处, 南阳 473000)
0 引言
随着网络技术的不断发展,越来越多的人选择使用互联网,尤其是我国互联网络的用户数量增长速度更快,同时网络安全问题也随之而来,人们从各个层次构建网络安全防范措施[1]。如数据包加密、访问认证、入侵检测等,其中数据包加密、访问认证属于被动防御,可以检测、拦截大多数入侵行为,但是无法检测、拦截网络系统内部的入侵行为,网络入侵检测可以对网络系统的信息进行分析,可以对系统内部的入侵行为进行检测,因此相对于数据包加密、访问认证,入侵检测可以更加有效的保证网络安全,因此成为当前网络安全管理领域中的主要研究内容[2]。
到目前为止,许多专家和学者对网络安全管理问题进行了研究,取得相当大的研究进展,涌现了许多入侵检测检测方法[3,4]。当前网络入侵检测技术分为滥用检测和异常检测两种,其中异常检测可以检测到新的入侵行为,因此大多数网络系统通过异常检测进行安全保护[5]。当前网络入侵异常检测基于聚类分析算法、神经网络等,但是聚类分析算法的网络入侵异常检测速度快,但是网络入侵异常检测错误率比较高,神经网络的网络入侵异常检测正确率高,但是由于网络入侵行为的特征维数比较多,易出现“维数灾”难题,因此网络入侵异常检测仍然面临挑战[6-8]。支持向量机(SVM)是近年来兴起的分类技术,可以将网络入侵异常检测看作是一种多分类问题,通过其自学习构建网络入侵异常检测模型,为网络入侵异常检测提供了一种新研究的工具[9]。然而支持向量机的性能与其参数直接关联,当前主要通过经验方法确定相关参数,参数的合理性难以得到有效保证。而粒子群算法是一种随机搜索算法,可以对支持向量机参数确定问题进行求解[10]。
针对当前网络入侵检测存在误检率大、漏检率高,检测实时性差等不足,以改善网络入侵检测效果为目标,设计了粒子群算法和支持向量机的网络入侵检测方法,并采用网络入侵检测的标准数据集进行仿真测试,分析本文方法的有效性。
1 粒子群算法和支持向量机
2.1 粒子群算法
粒子群算法源于对鸟群觅食行为,粒子的状态由位置和速度两个矢量决定,第i个粒子的速度向量为vi=(vi1,vi2,…,viD),第i个粒子在第t和t+1个时刻的位置为vi(t)和vi(t+1),vi(t)和vi(t+1)之间的关系为式(1)。
vi(t+1)=wvi(t)?+c1r1(pi(t)-xi(t))+c2r2(g(t)-xi(t))
(1)
式中w为惯性权值,用于平衡个体全局和局部搜索能力,c1,c2为两个加速度常数,r1,r2为两个随机数,pi(t)表示粒子i在第t个时刻历史最优位置,那么在第t+1个时刻,其变化方式如式(2)。
(2)
式中f(·)表示适应度函数。
g(t)表示粒子群在t时刻的全局最优位置,其确定方式为式(3)。
(3)
式中N表示种群粒子的个数。
第i个粒子的位置向量为xi=(xi1,xi2,…,xiD),第i个粒子在第t和t+1个时刻的位置为xi(t)和xi(t+1),它们之间的关系为式(4)。
xi(t+1)=xi(t)+vi(t+1)
(4)
粒子群算法的基本工作流程如图1所示。
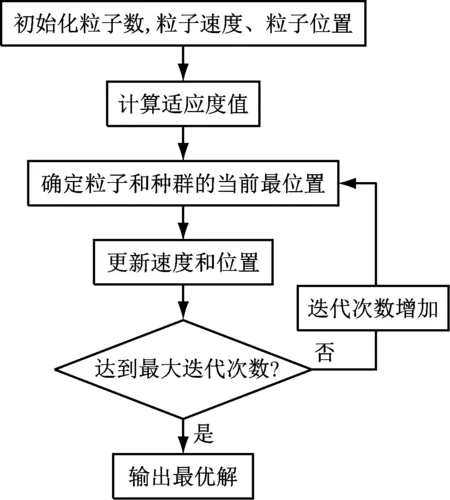
图1 粒子群算法的基本工作流程
2.2 支持向量机
传统机器学习如神经网络等,基于经验风险最小化原理进行学习,支持向量机与其它机器学习算法的工作原理不一样,基于结构风险最小化原理进行学习,当样本数量比较小时,仍然可以获得较好的泛化能力,不仅解决了传统机器学习在样本数量比较小时易出现“过拟合”的学习结果,而且不存在“维数灾”缺陷。对一个二分类问题,其训练样本组成的集合为{xi,yi},i=1,2,…,n,其中xi为样本的输入向量,yi表示样本的实际输出,n为样本的总数,支持向量机引入映射函数φ(·)对{xi,yi},i=1,2,…,n进行变换,然后对其进行求解,建立最优分类超平面,具体为式(5)。
f(x)=ωT×φ(x)+b
(5)
式中,ω和b分为权值矢量和阈值矢量。
要建立最优分类超平面,首先要确定ω和b的值,对ω和b进行直接求解很难,求解时间长,空间复杂度高,为此基于结构风险最小化原则,对最优分类超平面进行如下限制为式(6)。
yi×(ωT×φ(xi)+b)≥1
(6)
在最优分类超平面的附近,有一些样本分类结果有一定的误差,为了允许这些误差的存在,引入非负松弛变量ξi提高支持向量机的学习能力,那么可以得到式(7)。
(7)
式中,C为惩罚参数。
用Lagrange乘子对式(7)进行再次变换,建立如下形式的最大优化问题为式(8)。
(8)
相应的约束条件为式(9)。
(9)
由于网络入侵检测特征向量和入侵行为的类型之间存在的一定的随机性和非线性,为此引入核函数k(xi,x)=φT(x)φ(xi),那么式(8)变为式(10)。
(10)
式中,αi对应的样本为支持向量,其数量远远小于训练样本数。
网络入侵检测的支持向量机最优分类平面可以描述为式(11)。
(11)
其中,核函数定义如式(12)。
(12)
式中,σ表示核宽度。
上述过程为二分类问题求解的支持向量机工作原理,然而网络入侵行为一般有4类,包括正常行为,则共有5类,这样基本支持向量机无法求解,为此通过一对多的形式建立网络入侵检测的支持向量机多分类器的结构,具体如图2所示。
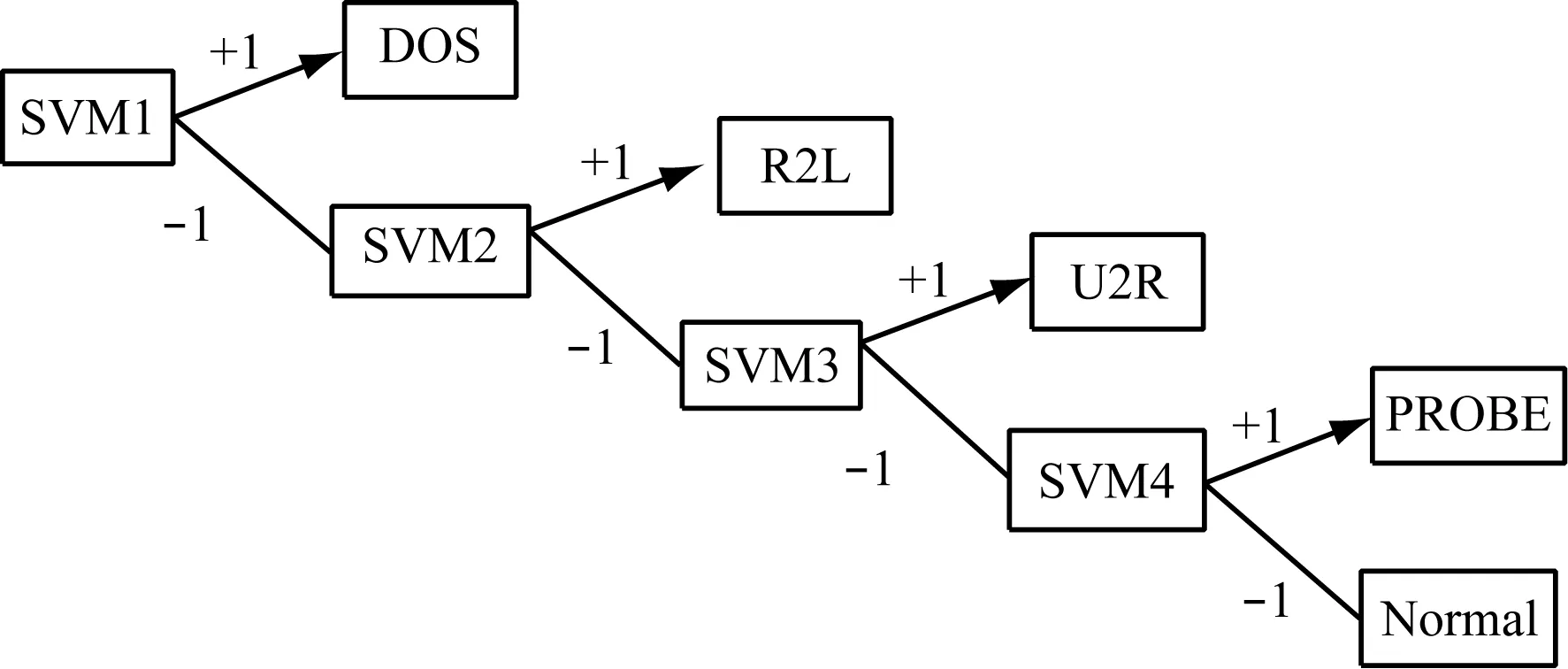
图2 网络入侵检测的支持向量机多分类器的结构
3 粒子群算法和支持向量机的网络入侵检测步骤
(1) 从网络系统中采集通信数据,并从通信数据提取网络入侵检测特征。
(2) 根据网络入侵检测特征,根据专家系统确定网络入侵行为的类型。
(3) 将网络入侵检测特征作为输入向量,网络入侵行为的类型作为输出向量建立样本数据集。
(4) 从网络入侵样本数据随机选择部分数据组成训练样本集合,并随机选择部分数据组成验证样本集合。
(5) 支持向量机对训练样本集合进行学习,通过粒子群算法确定参数C和σ的值,建立网络入侵行为检测的分类器。
(6) 采用验证样本集合对网络入侵行为检测分类器的性能进行测试,并输出和分析测试结果。
4 网络入侵检测的实例分析
为了分析粒子群算法和支持向量机的网络入侵检测性能,采用网络入侵检测标准数据集KDD 1999作为研究目标,KDD 1999的样本数量相当多,为此从中随机选择部分样本进行仿真实验,网络入侵行为以及样本数量分布具体如表1所示。
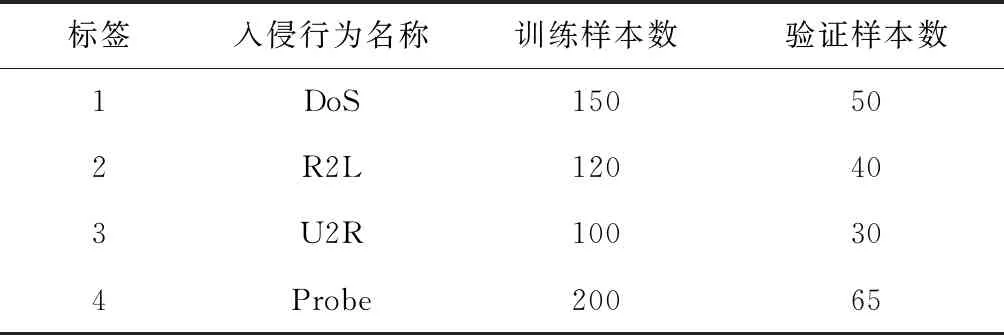
表1 网络入侵行为以及样本数量
设置粒子群算法相关参数,具体如表2所示。

表2 粒子群算法的相关参数设置
然后通过粒子群算法确定参数C和σ的值,它们分别为187.65和1.783。
选择文献[7]的网络入侵检测方法和文献[8]的网络入侵检测方法进行对比实验,统计它们的网络入侵检测正确率和训练时间(秒),结果如图3和图4所示。
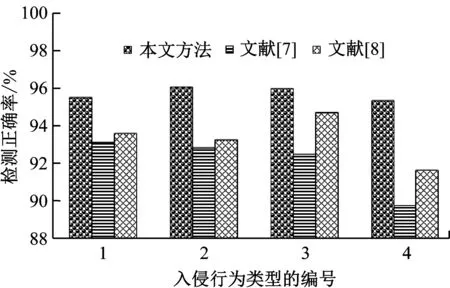
图3 与文献[7]和文献[8]的入侵检测正确率对比

图4 与文献[7]和文献[8]的训练时间对比
从图3和图4可以看出,相对于文献[7]和文献[8]的网络入侵检测方法,本文方法的网络入侵检测正确率更高,这表明网络入侵检测的误检率、漏检率减少,网络入侵检测效果更优。
(2) 相对于文献[7]和文献[8]的网络入侵检测方法,本文方法的网络入侵检时间明显减少,降低了时间复杂度,可满足网络入侵检测实时性要求。
5 总结
为了提高网络入侵检测性能,引入支持向量机对网络入侵检测进行建模,并引入粒子群算法优化支持向量机参数,最后采用KDD 99数据进行了仿真实验,实验结果表明本文方法获得了理想的网络入侵检测效果。

