EEMD 修正爆破加速度零漂信号中的最优白噪声系数*
王志亮,陈贵豪,黄佑鹏
(合肥工业大学土木与水利工程学院,安徽 合肥 230009)
在岩石钻孔爆破过程中,爆源近区岩石的冲击振动信号具有持时短、频带宽的特点[1]。目前广泛使用的压电式加速度传感器在采集此类信号时,大多会出现“零漂”现象[2-6]。造成压电传感器出现零漂误差的原因主要有[2-3]:(1)受到高频冲击波作用时,传感器由于自身谐振反应导致内部压电晶体磁畴变化,这种变化反映到输出信号上,出现零漂现象;(2)高冲击作用下,传感器压电元件受到的作用力超过其在装配时受到的预压力,进而造成压电晶体与惯性质量块之间出现微量运动,造成零漂现象;(3)传感器的质量-弹簧系统受到高冲击作用时的动刚度不足会导致其幅值线性度变差,可能造成零漂;(4)受限于传感器压电材料和制造工艺,信号放大器电路易过早进入饱和堵塞状态,RC 电路放电时间延长到冲击结束后,表现为零漂;(5)传感器基座与被测物体表面连接刚度不足造成零漂误差。由于爆破过程中岩石结构会产生不可逆的损伤,因而每次爆破信号的采集是单次性的。所以,如果爆破振动信号采集过程中出现零漂现象,采用合理方法对误差信号进行修正非常有必要[4-6]。
近年来,不少学者对于零漂信号中产生的趋势项去除方法进行研究:龙源等[6]基于经验模态分解(empirical mode decomposition, EMD)、小波法、最小二乘法分别研究了爆破震动测试信号中趋势项的去除算法,并对三种方法去除趋势项效果及重构信号的时频特征进行对比分析,指出多项式趋势项中的多项式阶数选取对于信号的修正效果有较大影响;王燕等[7]采用EMD 法和最小二乘法相结合,以侵彻结束后的零漂趋势作为侵彻过程中的零漂趋势,对侵彻不同介质的实测过载数据进行去除零漂的处理,通过对修正后的过载数据进行一次积分和二次积分,得到的侵彻速度和位移与实测结果吻合较好;王济[8]研究发现滑动平均法应用较为简便,但其本质仅是为了曲线基线回归零点,在处理信号时有一定的盲目性;谢全民等[9]认为小波法需要针对振动信号特点事先选取合适的小波基函数和分解层数;吴祖堂等[10]通过理论分析和实验验证得出冲击结束后的压电式传感器信号呈指数形式衰减的结论,但是信号的零漂往往在冲击信号达到峰值前就已经形成,冲击结束后信号的指数衰减规律和冲击过程中的趋势项类型是否一致,目前尚无定论;Huang 等人[11]揭示EMD 方法及其改进算法—集合经验模态分解(ensemble empirical mode decomposition, EEMD)方法的基函数都来自于其信号本身,对于信号的先验性信息要求较低,在处理爆破冲击这类非平稳信号时优势明显。实际上,EEMD 方法在EMD 方法基础上,通过添加在频谱上均匀分布的白噪声有效地解决了EMD 方法分解得到的固有模态分量(intrinsic mode function, IMF) 中存在的模态混叠和端点震荡问题[12],故认为EEMD 方法处理零漂信号的效果优于EMD 方法。但EEMD 方法中需要给出添加白噪声的系数,目前没有确定的量化指标去评价零漂信号的修正效果,从而无法确定白噪声系数的合理取值范围。
基于此,本文先给出不同白噪声系数下EEMD 结合高低频处理方法修正岩石爆破中加速度零漂信号的过程;再辅以冲击响应谱分析,提出表征修正前后频域平均偏差幅度的修正指数;在修正指数分析的基础上确定EEMD 修正爆破零漂信号中白噪声系数的最优取值范围,再用加速度信号积分后的速度信号对比讨论最优噪声系数范围的合理性,最后对比EEMD 法与滑动平均法,讨论二者的优点与不足。
1 算法原理
EEMD 是针对EMD 算法中所存在的不足进行改进的算法,EMD 算法实现过程如图1 所示[11]。EEMD 主要利用高斯白噪声在频谱上均匀分布的特性来弥补原始信号中一些缺失的尺度,使得不同时间尺度的信号自动分解到其相适应的参考尺度上去,从而有效地抑制EMD 分解信号时存在的模态混叠问题。由于添加的白噪声总体均值为零,所以将多次添加白噪声后所求得的IMF 分量的集合平均值作为最终结果,以抵消白噪声对于真实IMF 分量的影响。

图 1 EMD 算法流程图Fig. 1 Flow chart of EMD algorithm
EEMD 算法的实现步骤如下[12]。
(1) 将随机高斯白噪声信号nj(t)添加到原始信号x(t):
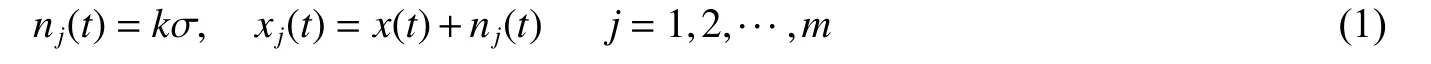
式中:xj(t)是第j 次加噪信号,k、m 分别是添加白噪声的系数和总次数,σ 是原始信号的标准差。
(2) 用EMD 方法将xj(t)分解成一系列IMF 分量ci,j和余项δj:
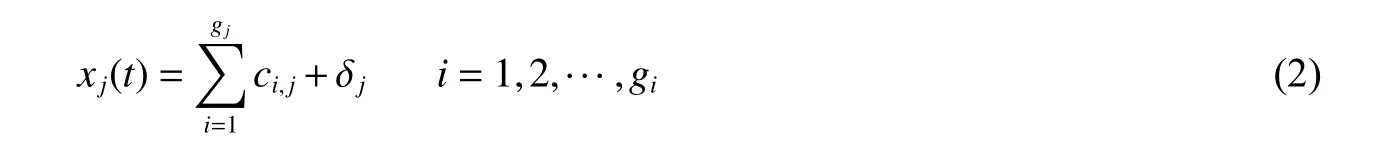
式中:ci,j和δj分别为第j 次加入白噪声后信号分解得到的第i 个IMF 分量和余项,gj为第j 次加入白噪声后信号的分解尺度。
(3) 如果j<m,则重复步骤(1)和(2)。
(4) 获取I=min(g1, g2,···, gm),计算I 相应的分解的IMF 的集合平均值作为最终结果:
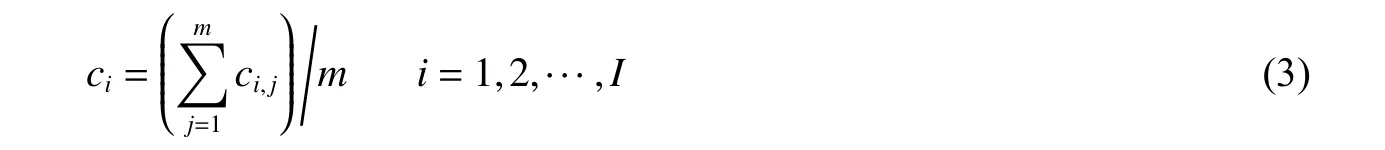
2 信号处理
2.1 信号介绍
本文所处理的零漂信号来源于花岗岩爆破试验,其数据采集过程和时程曲线分别如图2 和图3 所示。爆源为1.5 g 太安炸药,爆速约为6 000 m·s−1。图3 中加速度信号A 测点的爆心距约为60 cm。信号放大器的采样频率为5×105Hz,加速度传感器的频响范围是40~4×104Hz,设置低通3×104Hz。由图3可以看出峰值加速度超过了4×104m·s−2,同时加速度信号在冲击结束后没有迅速归零,而是持续一段时间后才缓慢归零,这是高速冲击环境下的典型零漂信号。

图 2 试验与数据采集Fig. 2 Test and data collection

图 3 爆破加速度信号AFig. 3 Blast acceleration signal A
2.2 白噪声系数范围
Wu 等[12]在分析EEMD 理论时,建议k 近似取0.20;Jiang 等[13]用EEMD 方法对振动信号分析时指出,如果信号主频段由高频分量组成,则k 的取值范围建议为0~0.20。
岩石的爆破试验结果表明[14-15],岩石质点的振动主频率与炸药装药量成反比关系,与炸药爆速成正比关系;装药深度对振动主频率也有很大影响,深孔爆破产生的地震波主频较低,浅孔爆破产生的地震波主频较高。本文爆破试验的装药量小、深度浅、炸药爆速大且传播距离短,故认为其主频段主要由高频分量组成。因此,白噪声系数k 选在0~0.20 范围内讨论。
2.3 修正过程
2.3.1 EEMD 分解
为分析白噪声系数对于EEMD 方法修正零漂信号的影响,在0~0.20 范围内选取0.05、0.10、0.15 和0.20 四个k 值对应的白噪声添加到原始信号中进行EEMD 分解,添加次数均为100 次。图4 给出k=0.10 时分解得到的IMF 分量和余项δ。
2.3.2 IMF 分量频谱分析
将分解得到的IMF 分量分别进行FFT 变换,可得各IMF 分量的频谱信息。不同白噪声系数下分解得到的各IMF 分量的主频如表1 所示。限于篇幅,仅给出部分IMF 分量的频谱图,如图5 所示。
从表1 可以看出,白噪声系数对前两阶IMF 分量的主频影响很小,前两阶IMF 分量主频均在18 800 Hz 左右。结合图5(a) 可知,白噪声系数主要影响其主频幅值,系数越大,主频幅值越小;从IMF2 至IMF11 分量,随着分解阶数的增加,IMF 分量主频迅速衰减,且不同白系数噪声下分解的同阶IMF 分量主频与白噪声系数呈现正相关关系;IMF11 之后的分量的主频降至低频段,且基本保持不变。同时,从图5 可看出,相同白噪声系数下分解得到的IMF 分量随着分解阶数增加,其频段降低,频带渐窄。
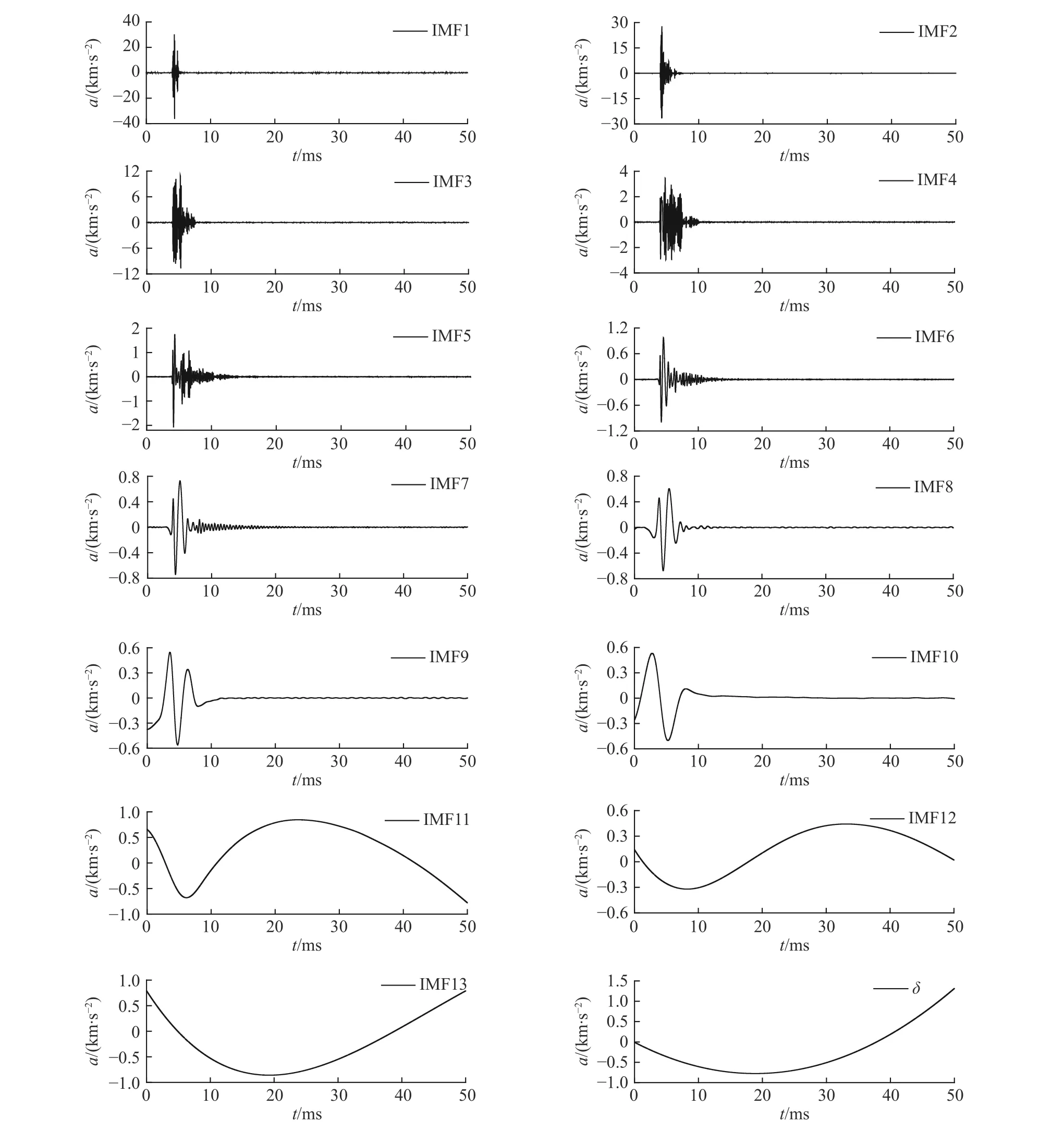
图 4 EEMD 分解信号(k=0.10)Fig. 4 Signals decomposed by EEMD method (k=0.10)
2.3.3 IMF 分量处理
(1)低频处理。由表1 知,IMF11 至IMF13 分量和余项δ 的主频集中在40 Hz 以下,低于试验中加速度传感器的频响下限 (40 Hz),故认为其可信度很低。因此,将IMF11 至IMF13 分量和余项δ 消除。
(2)高频处理。由于原始信号就含有大量高频噪声,故对不同白噪声系数下的IMF1 至IMF10 分量分别进行小波阈值去噪处理,阈值由heursure 函数自适应获取,去噪方式采用软阈值处理[16-17]。
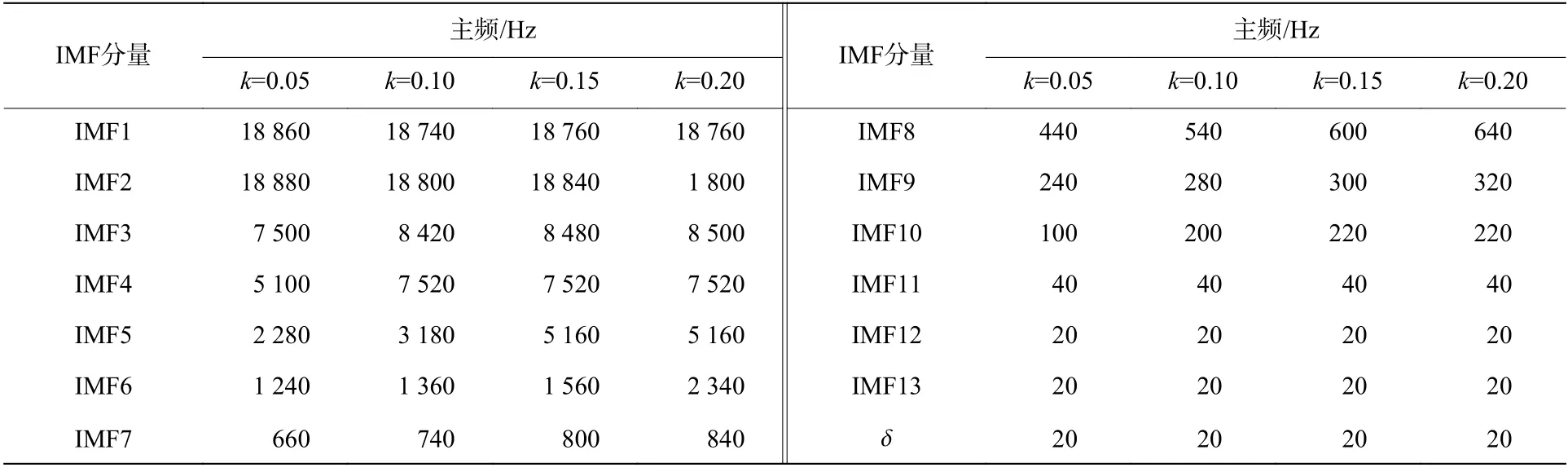
表 1 不同白噪声系数下IMF 分量主频Table 1 Dominant frequencies of IMF components under different white noise coefficients
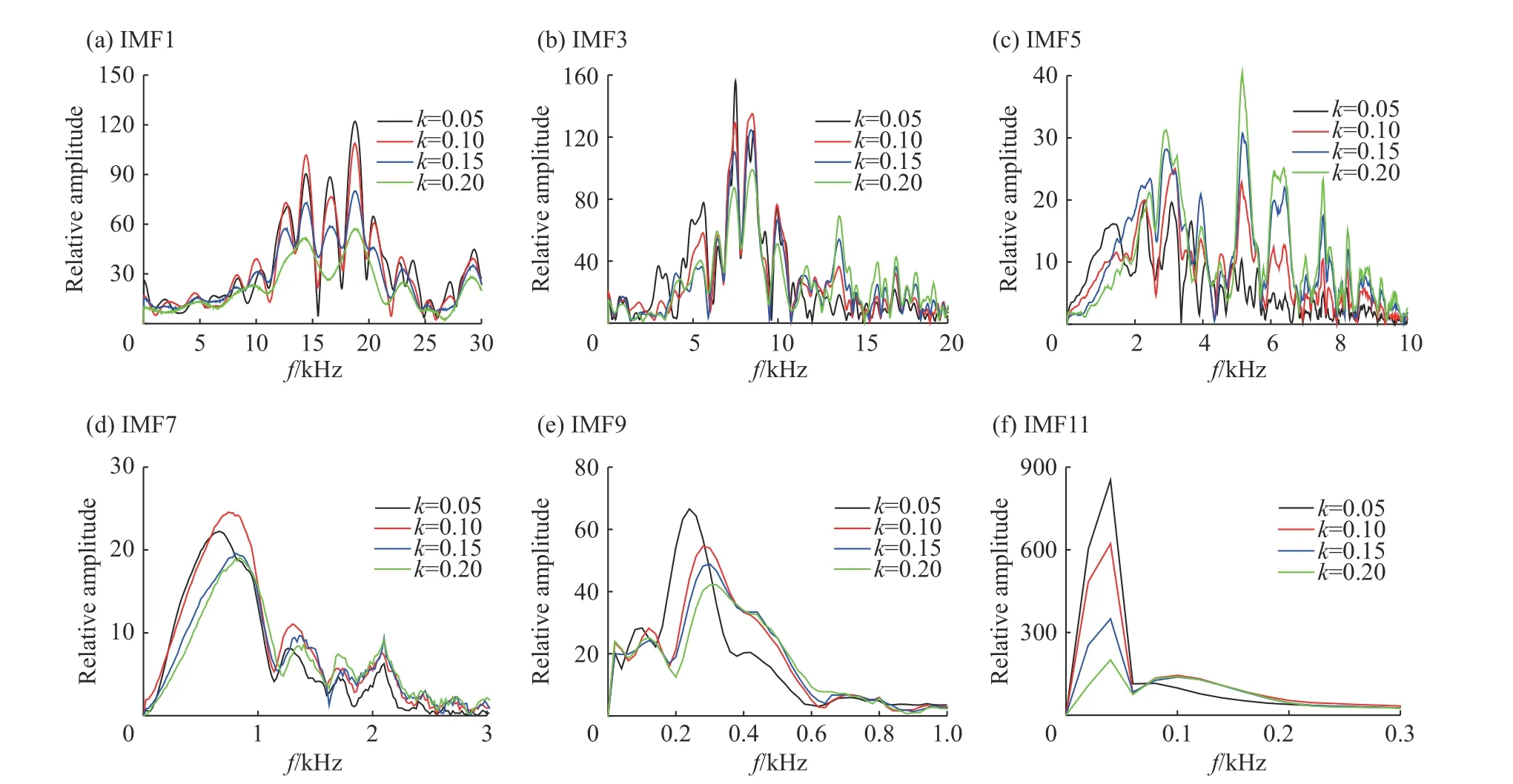
图 5 部分IMF 分量频谱图Fig. 5 Spectrograms of partial IMF components
分别对处理过的分量IMF1 至IMF10 进行重构,即可得到不同白噪声系数下EEMD 修正后的爆破冲击信号。信号A 修正后的四个加速度信号都很好地消除了零漂趋势,但由于彼此在加速度时程图上的波形差异很小导致难以区分,故仅给出白噪声系数为0.10 时的修正信号,如图6 所示。
3 修正信号分析
3.1 频域分析

图 6 EEMD 修正前后的信号Fig. 6 Signals before and after EEMD correction
图7 给出了修正前后信号的冲击响应谱。从冲击响应谱上来看,四个修正的信号与原始信号A 的频域“差异”主要集中在4 000 Hz 以下。在4 000 Hz 以上的频段,修正前后的频域“差异”不明显,很好的保留了原始信号的峰值和变化规律。需要指出,这里的“差异”是指处理后的信号与原始信号在冲击响应谱幅值上的相对偏差度,而非绝对偏差值。由于40 Hz 以下频段已经超出加速度传感器的频率响应范围,这部分原始信号认为是不可信的,采用的修正方法应将这部分的信号尽可能削弱,同时应该尽量保留中高频段可信信号的频谱特征。因此,为兼顾防止信号中高频段过度修正和尽量削弱低频失信段的目的,需要定义一个具体指标来评价信号的修正效果。
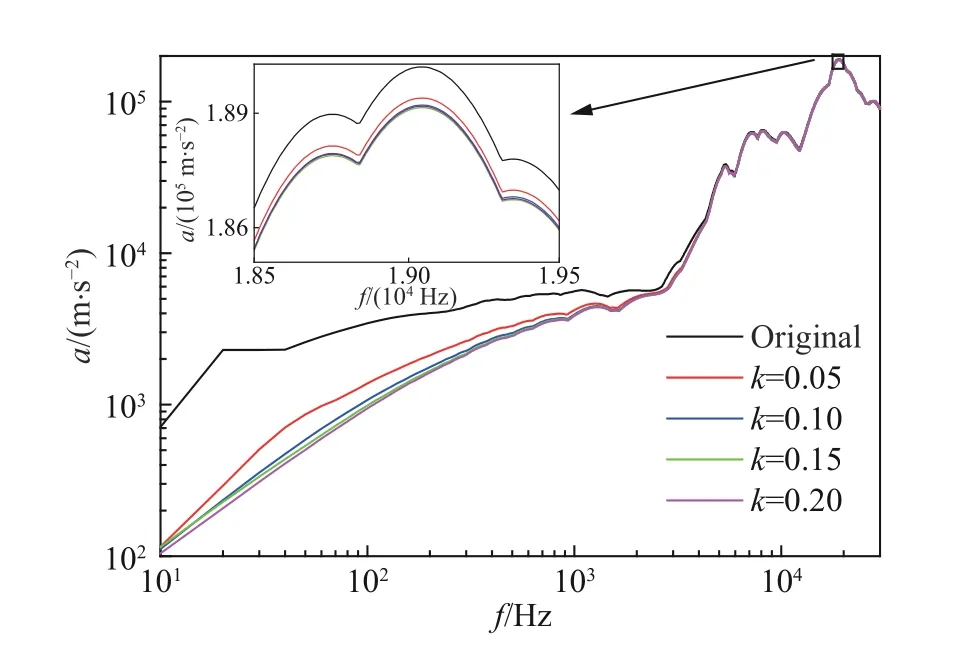
图 7 不同白噪声系数下EEMD 修正信号的冲击响应谱Fig. 7 Shock response spectra of signals modified by EEMD under different white noise coefficients
3.1.1 修正指数定义
设所选频段的频率序列为{f1, f2,···, fl},对应的冲击响应谱序列为{P1, P2, ···, Pl},其中f 为频率,P 为每个频率对应的冲击响应谱幅值,l 为频段的频率点总数。则反映信号修正前后冲击响应谱平均偏差幅度的修正指数定义如下:

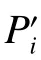
3.1.2 指数应用
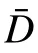
为了评价不同白噪声系数下信号在不同频段上的修正效果,在(0, 0.20]中以0.001 为间隔取200 个k 值进行信号处理。原始信号A 在这些白噪声系数下处理后,可得200 个修正信号。然后,将这些修正信号与原始信号的冲击响应谱代入式(5)计算,即可得到不同白系数噪声下相应频段的修正指数,如图8 所示。在给出的五个频段上,修正指数与白噪声系数都呈现近似幂指数的关系,可假定修正指数与白噪声系数的函数关系为:

式中:a0、a1、和b 为常数。

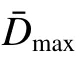
结合图8 与表2,对不同的噪声系数k 取值范围作如下讨论:
(1) 0<k<k1。在此区间内,失信频段上的修正指数随白噪声系数变化的幅度很大,拟合函数最大值小于相应的修正指数上限值的88%。故认为在此区间失信频段修正效果不够稳定,且对信号失信频段的削弱效果不足,不满足处理方法对于较好去除其低频趋势项的要求。
(2) k1≤k≤k2。在此区间内,失信频段上的修正指数随白噪声系数变化的幅度相比于前一区间减小很多。修正指数平均值达到80.63%,比失信频段的修正指数下限8.86%提高了810%,已经达到修正指数上限值的92.98%。虽然在置信频段及其三个分段上,修正指数会随着噪声系数取值区间的上升而增大,可能导致在这些频段上出现信号修正过度的问题,但在这四个频段上前后两个区间的修正指数平均值分别只相差0.69%、3.73%、0.30%和0.13%,修正指数上升的幅度不大。故认为这个区间内修正后信号较好地去除了低频信号,且在置信频段尤其是高频段的频域失真很小,是可以接受的。
(3) k2<k ≤0.20。这一区间与[k1, k2]区间相比,噪声系数的增大会使置信频段尤其是高频段的频域失真增大,但与此同时信号失信频段的削弱效果不能得到有效提升,白噪声系数增大的意义很小。
综上分析,可以确定信号A 对应的最优的白噪声系数k 取值区间为[0.256,0.066]。
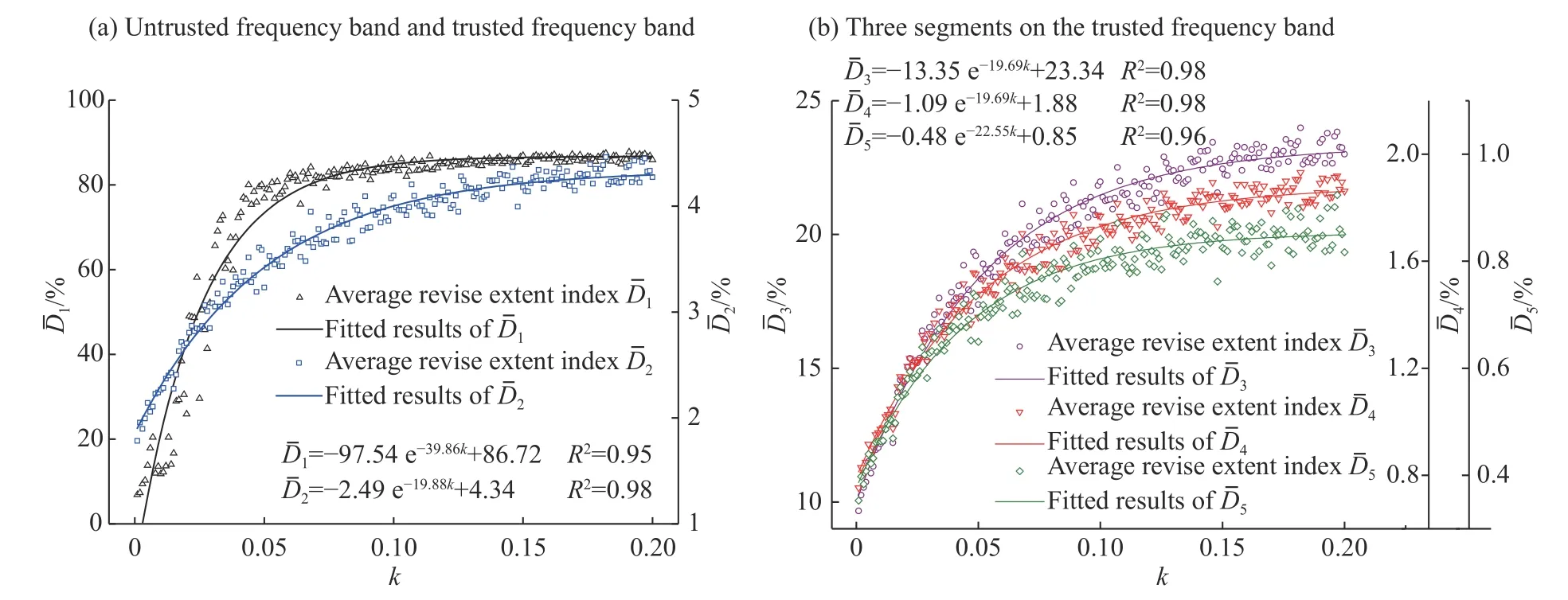
图 8 不同白系数噪声下不同频段上的冲击响应谱修正指数Fig. 8 Correction indices of shock response spectra on different frequency bands under different white noise coefficients

表 2 不同频段修正指数范围Table 2 Ranges of correction index on different frequency bands
3.1.3 修正指数验证
通过图9 看出,随着噪声系数的提高,EEMD 方法修正后信号与原始信号B 在冲击响应谱上的差异呈上升趋势,修正指数与噪声系数依然呈现如式(5) 的幂指数函数关系。但是当噪声系数k 上升到0.10 之后,EEMD 方法对失信频段0~40 Hz 上信号的频域削弱几乎不再增加,但是对于置信频段上的三个分段上信号的频域削弱依然在增加,这也就意味着在(0.10, 0.20)范围内,增大噪声系数不能进一步削弱失信频段信号,反而会导致修正后信号在中高频失真加大。如采用3.1.2 节中的方法,同样可以确定一个大致的最优噪声系数取值范围,即为[0.098,0.114]。
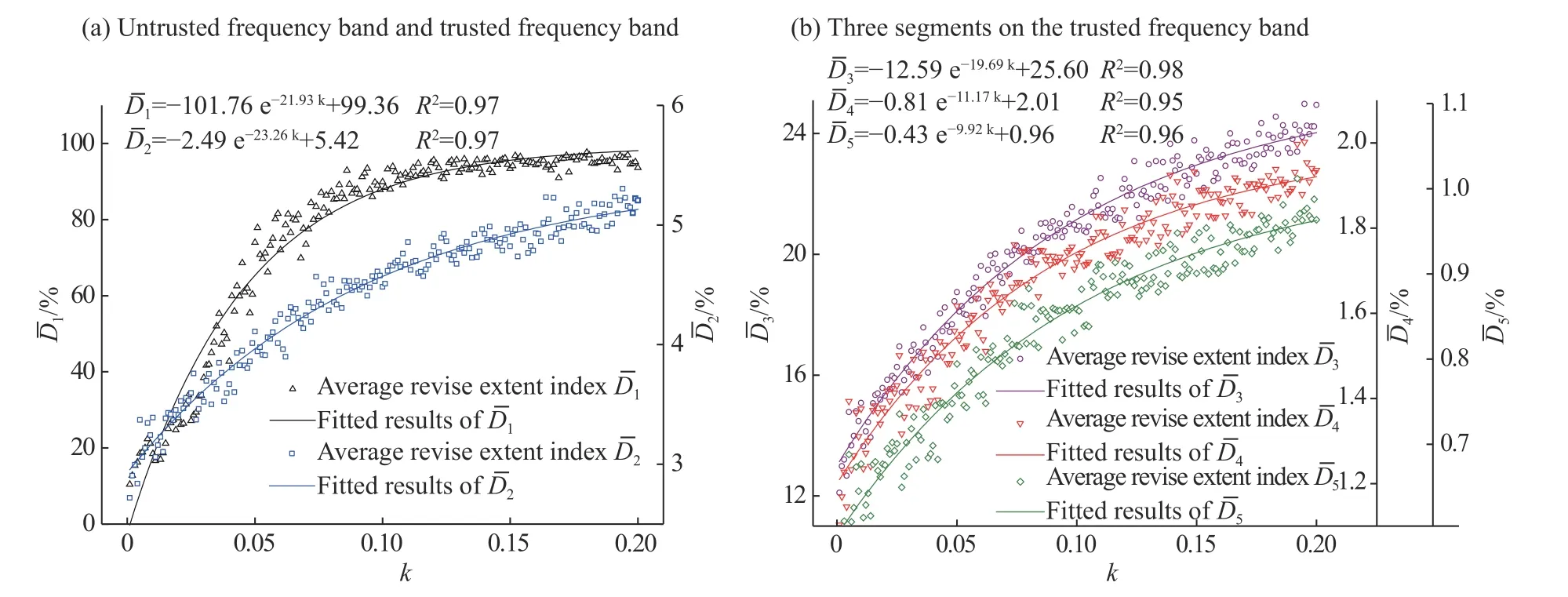
图 9 不同白系数噪声下不同频段上的冲击响应谱修正指数Fig. 9 Correction indices of shock response spectrum on different frequency bands under different white noise coefficients
3.2 时域分析
从图3、图6 和图10 中可以看出,仅从加速度零漂信号本身来说,EEMD 处理零漂信号A 和B 后得到的信号均很好地去除了原始信号中的零漂趋势项,其波形在爆破冲击结束后都很快回归基线,保留了原始爆破信号的衰减特征。
事实上,零漂偏差在加速度信号上表现得不如加速度时域积分后得到的速度信号显著,这是因为不仅加速度信号基线漂移会导致积分后速度信号基线漂移严重,而且原始信号上下振幅的不对称也会加剧积分曲线漂移。因此,对于加速度信号A 及其在不同白噪声系数下处理得到的修正信号进行积分,得到的速度信号如图11 所示。

图 10 爆破加速度信号B 及其修正信号Fig. 10 Blast acceleration signal B and its corrected signal
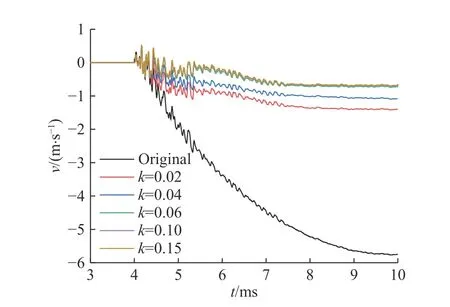
图 11 EEMD 修正前后速度曲线Fig. 11 Velocity curves before and after correcting by EEMD
图11 表明EEMD 方法对于速度信号的零漂失真有明显改善:随着白噪声系数的提高,修正后的速度曲线逐渐靠近零点。当k 值大于0.60 时,EEMD 对于速度信号的零漂修正效果几乎没有变化,这也与图7(a)中失信频段的修正指数分布图相契合。同时,这也表明通过修正指数分析确定信号A 的最优白噪声系数范围[0.056,0.066]是合理的:将白噪声系数范围上调已经不能明显改善速度曲线零漂趋势;而将白噪声系数范围下调,速度曲线明显随之下滑,零漂趋势加重。但是,图11也表明了EEMD 修正后的速度曲线无法完全消除零漂趋势,优化的噪声系数也很难让速度曲线基线完全回归零点。
3.3 进一步讨论
以上的分析表明,EEMD 对于积分后的速度信号的零漂趋势去除得不够完善,存在一定的局限性。仅是考虑让积分后速度信号基线完全恢复到零点上,滑动平均法是一种简单有效的方法。影响滑动平均法去除信号零漂趋势的因素有两个[8]:平滑点数和滑动阶次。对加速度信号A 进行平滑点数为20 和滑动阶次为10 的滑动平均法处理,处理后的信号积分得到速度曲线如图12 所示。图11 和图12 对比显示,滑动平均法得到的速度曲线是优于EEMD 的,更符合爆破速度曲线的振动特征。
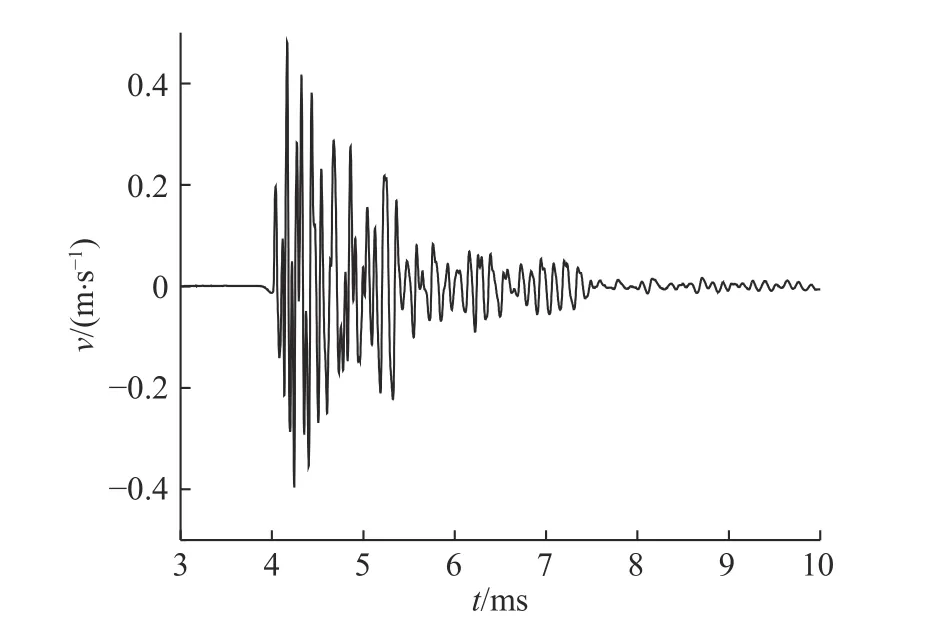
图 12 滑动平均法修正后速度曲线Fig. 12 Velocity curve modified by sliding average method
通过图13 给出的原始信号以及两种方法处理后信号的冲击响应谱,发现滑动平均法相对于EEMD 方法在各个频段上频域损伤均更大。而冲击响应谱的低频部分,往往反映了岩石自身大的位移或者应变,其主要是由于零漂误差还是岩石自身的动力响应造成,还难以界定。所以,尽管滑动平均法很好地去除加速度信号积分后的速度信号的零漂趋势,但这也会使得修正信号的频谱失真加重以及岩石自身的动力响应削弱。
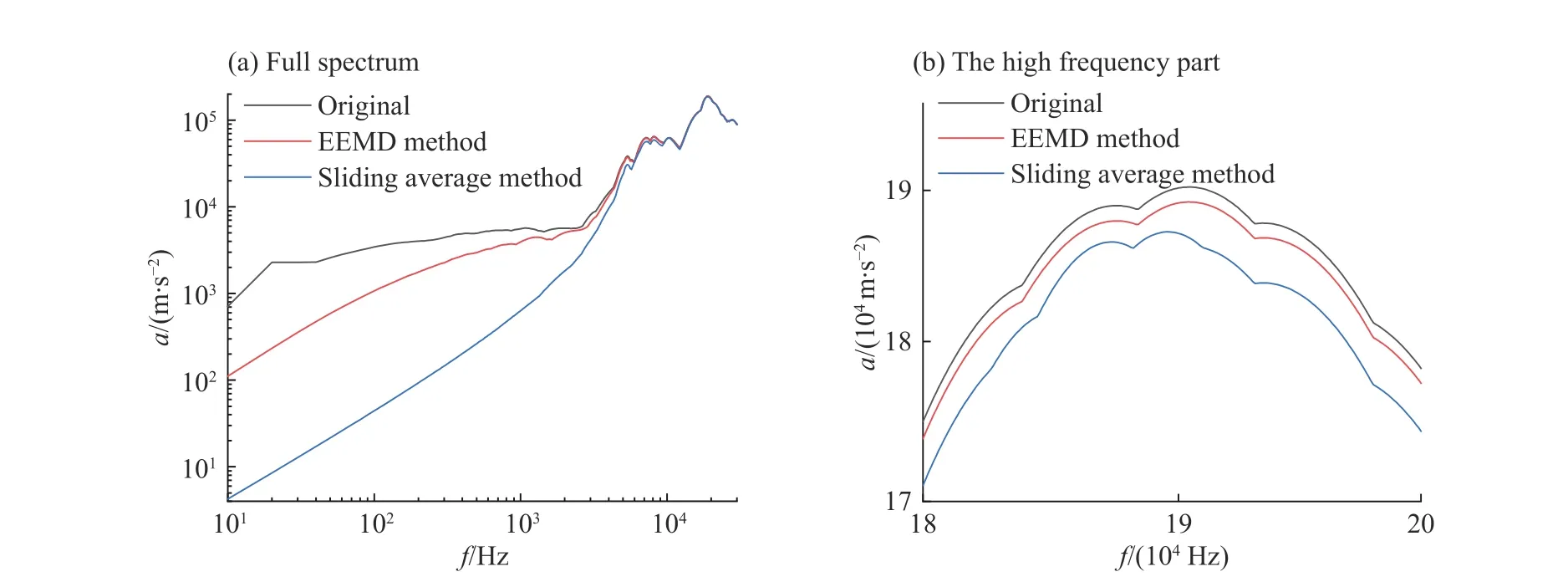
图 13 两种方法处理后信号与原始信号的冲击响应谱Fig. 13 Shock response spectra of original signals and processed signals by the two methods
4 结 论
本文结合花岗岩的室外小型爆破试验,对EEMD 修正爆破零漂信号中最优白噪声系数范围进行了探析,得出主要结论如下:(1)利用EEMD 方法并结合高低频处理能够较好地去除爆破加速度信号的零漂趋势,是一种自适应且高效的处理方法;(2)基于冲击响应谱定义的修正指数,能够较好地反映信号修正前后在冲击响应谱不同频段上的平均偏差幅度;随着白噪声系数增大,不同频段上修正指数均不同程度上升,二者呈现相关性较高的幂指数函数关系;(3)通过修正指数并结合对现场测试传感器的频响范围分析,确定出加速度零漂信号对应的白噪声系数的最优取值范围,优化的噪声系数使得EEMD 法在最大程度削弱信号零漂趋势的同时尽量保留信号的频谱信息;(4)优化EEMD 法中的噪声系数只能改善加速度积分后速度信号的零漂趋势而无法将其彻底去除;相对应的滑动平均法在速度信号的零漂修正效果上表现更好,但同时也带来了修正前后频谱差异加大以及动力响应的过度削弱的问题。

