钨合金柱形弹超高速撞击水泥砂浆靶的侵彻深度研究*
钱秉文,周 刚,李 进,李运良,张德志,张向荣,朱玉荣,谭书舜,景吉勇,张子栋
(西北核技术研究院,陕西 西安 710024)
近年来,美军提出了“全球快速打击”计划,研制了X-43、X51 和HTV-2 等超高速飞行器,末端速度达到2 km/s 以上,使“上帝之杖”等武器概念成为可能。现阶段可供借鉴的超高速撞击实验研究大多集中在空间碎片防护和超高速穿甲方面,与超高速撞击地介质的差异较大。但目前部分学者开展了少量的超高速撞击地介质实验,王明洋等[1]、李干等[2]开展了高强钢弹体超高速撞击混凝土靶和岩石靶的实验研究,并在此基础上初步建立了超高速长杆弹侵彻、地冲击效应的理论模型。牛雯霞等[3]开展了弹体超高速撞击多层混凝土靶的实验研究,获得了开坑形貌和开坑后破片群的扩展图像。张浩等[4]开展了金属球弹撞击混凝土靶研究,重点分析了冲击融化现象。但目前国内外在超高速对地撞击问题方面,开展的实验研究并不系统充分,认识还比较粗浅,其毁伤机理、毁伤效应和毁伤模式等尚难以评估。学者们还采用数值模拟方法分析超高速撞击地介质问题。Antoun 等[5]用GEODYN 程序模拟了重金属弹体超高速侵彻石灰岩的效应,展示了超高速撞击的巨大毁伤威力。邓国强等[6]利用自行研制的软件模拟了超高速对地撞击的毁伤效应。以上数值模拟工作缺乏必要的实验验证,很难准确、全面地认识超高速对地撞击的毁伤机理和毁伤效应。此外,大尺寸、大质量(千克级以上)弹体的超高速撞击实验受限于加载设备,目前未见相关报道。超高速撞击地介质靶的尺度效应问题由于缺乏大尺寸弹体的超高速撞击实验数据,也未形成统一认识。因此本文并不讨论尺度效应问题,拟开展弹速2 km/s 以上的克级钨合金柱形弹超高速撞击水泥砂浆靶实验研究,结合CT 图像诊断技术获得成坑特性实验数据,利用实验数据修正数值模拟方法,结合实验结果和数值模拟结果探索克级柱形弹超高速撞击水泥砂浆靶的侵彻深度变化规律和机制。
1 实验安排
1.1 实验方法
实验在57/10 二级轻气炮上进行,装置示意图如图1 所示。实验时弹体由57/10 二级轻气炮发射进入靶室,首先经过激光测速区利用激光遮断法[7]测量弹体速度;然后通过强制脱壳器,使弹托与弹体强制分离;最后弹体撞击水泥砂浆靶。实验后取出靶板,利用CT 图像诊断技术测量成坑的特征参数。实验中采用四分幅高速相机拍摄弹体飞行和撞靶过程,四分幅相机最高帧频为2×105s−1,本实验使用的帧频为2.5×104s−1,快门时间为145 ns,闪光光源采用脉冲氙灯,四分幅相机和闪光光源均采用激光信号触发。
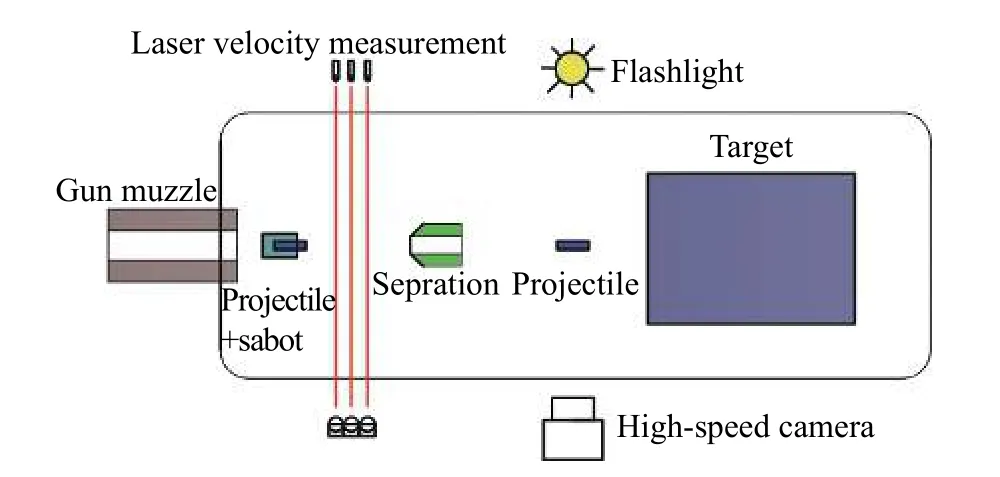
图 1 超高速撞击实验安排示意图Fig. 1 Experimental set-up for hypervelocity impact experiment

图 2 93W 钨合金柱形弹体和水泥砂浆靶Fig. 2 Cylindrical tungsten alloy projectiles and concrete targets
1.2 实验弹体
由于超高速撞击条件下毁伤效应和弹体密度密切相关,因此本文的弹体材料选用常见侵彻弹体材料中密度最高的93W 钨合金,密度为17.6 g/cm3,静态屈服强度为731 MPa。弹体为 ∅3.45 mm×10.5 mm的柱形弹体。实验弹体实物如图2 所示。
1.3 靶板设计
靶板的设计对实验的可信度有较大影响,我们重点关注的是靶板粗骨料选取和靶板尺寸选取。在粗骨料选取方面,为了尽量减少靶介质的不均匀性对撞击实验结果的影响,要求实验用靶板的粗骨料外径不大于弹身最小截面尺寸的四分之一[8],本文中实验弹体的直径为3.45 mm,粗骨料尺寸需控制在0.8 mm 以下。而普通混凝土的粗骨料尺寸太大,无法满足要求,因此选用沙粒尺寸不大于0.8 mm 的水泥砂浆代替含有粗骨料(石子)的混凝土作为靶体。水泥砂浆可以看做是没有粗骨料的混凝土,在成型及养护过程中,存在微裂纹、孔洞等缺陷,这些缺陷在应力作用下,会增殖、扩展、传播。因此,作为撞击毁伤的靶板材料,水泥砂浆与混凝土特征相似,可以用水泥砂浆靶代替混凝土靶。在靶板尺寸选取方面,王可慧[8]在弹速最高2.26 km/s 的高速侵彻实验中,认为靶板直径取为弹径的50 倍即可忽略靶板的边界效应。本文中考虑到超高速撞击条件下弹体对靶板横向破坏效应更加显著,靶板直径取为弹径的约85 倍(300 mm),且靶板外围采用3 mm 厚的钢圈加固。
制备混凝土靶(水泥砂浆靶)所用原材料为:425 普通硅酸盐水泥、细砂(砂粒尺寸不大于0.8 mm,用筛子多次筛选)、自来水。其质量配比为水泥∶砂∶水 =1∶2.6∶0.5,养护28 d 后的平均单轴抗压强度为42.7 MPa,制备的靶板如图2 所示。
1.4 弹托分离装置
二级轻气炮发射的弹体通常都是由弹托携带的,在发射过程中弹托对弹体起支撑和加速作用;在离开发射管之后,弹托需与弹体分离,分离后应使弹托碎屑对弹体的影响减小到最小。本文中设计了强制分离器,采用分离器直接撞击弹托的方式将弹托与弹体分离。经过多次实验调试后,能保证弹体着靶姿态满足实验要求,如图3所示。
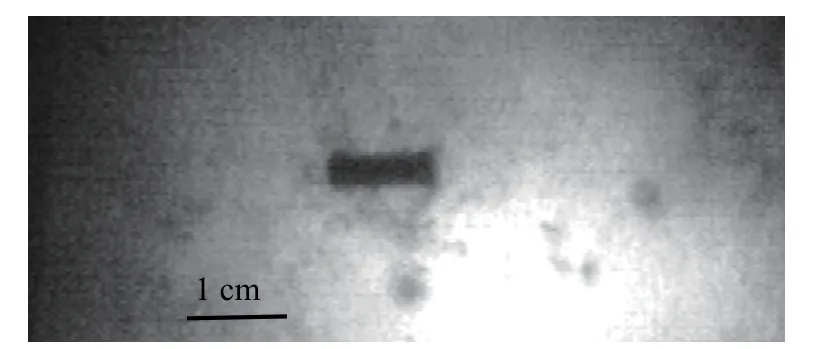
图 3 分幅相机拍摄的弹体飞行姿态Fig. 3 Framed photographs of projectile’s flight attitude
1.5 实验参数测量
弹体着靶速度测量采用激光光束遮断法,利用遮挡激光光束形成的时间间隔与光束间的距离得到弹速,经过长期校准,测速误差小于3%。
成坑特征参数的测量采用计算机层析成像(computerized tomography,CT)技术,CT 照片中(见图4),亮度和密度正相关,所以黑色的区域是弹坑、灰白色的区域是水泥砂浆靶体,明亮的白色是没有完全侵蚀的钨合金弹体。CT 扫描层间距为0.8 mm,通过CT 软件处理,可实现0.1 mm 的测试精度。利用CT 技术,可以得到精度较高的成坑特征参数,包括侵彻深度、成坑直径和成坑体积。

图 4 超高速撞击条件下靶板破坏CT 图像和成坑示意图Fig. 4 CT photographs and illustration of hypervelocity impacted crater
2 实验结果分析
为了探究超高速撞靶条件下钨合金弹体对水泥砂浆靶成坑机制,开展了克级钨合金柱形弹以1.82~3.66 km/s 的速度撞击水泥砂浆靶的实验。
图4 是不同速度下的成坑形貌和成坑示意图,可以看出水泥砂浆靶在超高速撞击条件下的成坑表现为“弹坑+弹洞”型。弹坑位于靶板表面,直径大、深度小。弹洞位于弹坑下方,口部直径较大,随着深度增加,弹洞直径逐渐减小。
成坑直径是表征横向毁伤效应的特征参数,成坑体积是表征横向和纵向破坏综合效应的特征参数。这两个参数是超高速撞击效应的重要表征,钱秉文等[9]已经对此进行了分析和总结,本文中重点关注侵彻深度和残余弹长的变化规律。
通过图4 中的不同速度下的成坑形貌可以看出:随着速度的增加,弹坑直径和弹坑深度逐渐增加,弹洞口部直径逐渐增加,侵彻深度先增大后降低。当弹速为1.97 km/s 时,弹体被侵蚀,残余弹长约为6.2 mm;当弹速增加至2.9 km/s 时,残余弹长降低至约3.2 mm;随着弹速继续增加至3.36 km/s,从CT 图像上都无法辨别高密度特征信号,说明弹体被完全侵蚀。侵彻深度和残余弹长是表征毁伤深度和弹体侵蚀的关键参数,因此将侵彻深度和残余弹长的测量参数列于表1 中。
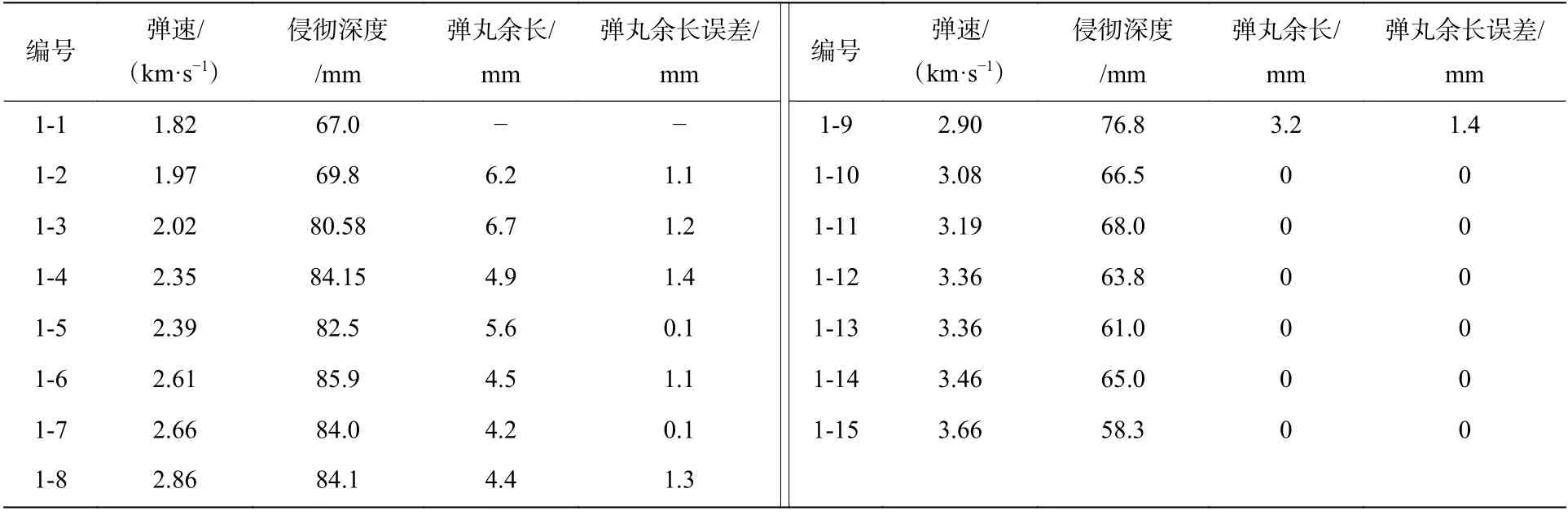
表 1 钨合金弹体超高速撞击水泥砂浆靶的成坑数据Table 1 Cratering data of hypervelocity impact of tungsten alloy projectiles penetrating concrete target
2.1 侵彻深度
侵彻深度随撞击速度变化关系如图5 所示。通过实验结果可以看出,超高速撞击条件下,侵彻深度并不是随着弹速提高而不断增加,而是在弹速2.6 km/s 附近存在一个侵彻深度的极大值。当弹速在2.6 km/s 以下时,随着弹速提高,侵彻深度逐渐增加;弹速在2.6 km/s 附近时,侵彻深度达到最大值,约8.5 倍弹长;当弹速高于2.6 km/s 时,随着弹速提高,侵彻深度逐步下降,但是当弹速高于3.2 km/s 时,侵彻深度下降幅度逐渐趋于平缓,当弹速为3.66 km/s 时,侵彻深度大约为6 倍弹长。王可慧[8]设计的侵彻结构弹在1 400 m/s 左右侵彻深度达到约为8 倍弹长。因此,如果仅比较侵彻深度,那么超高速弹体相对于中低速弹体在侵彻能力上并无显著优势。
2.2 残余弹长
超高速撞击条件下,弹靶界面会产生极高压力,远大于弹体材料强度,使撞击面附近的弹体材料发生侵蚀,并在弹头附近形成“蘑菇头”形状(见图6),这是超高速撞击条件下弹体的典型特征。图7 是残余弹体长度随撞击速度变化曲线,从图中可以看出,当弹速为1.97 km/s 时,残余长度为6.2 mm,侵蚀掉原弹长的约40%;随着撞击速度增加,弹体被侵蚀得越来越剧烈;当速度大于3.08 km/s时,弹体已经被完全侵蚀。
撞击初始时刻,弹靶界面产生极高压力,弹体发生侵蚀,靶板也在界面压力作用下逐渐开坑,该阶段称为“准定常侵彻阶段”。当弹体速度降低到弹靶界面压力不足以侵蚀弹体时,准定常侵彻阶段结束,此后“蘑菇头”形状弹体以刚体形式继续侵彻靶体,直至弹体速度降为0,该阶段称为“刚体侵彻阶段”。弹体以1.97 km/s 撞击靶板时,弹体并未完全侵蚀,说明弹体既经历了“准定常侵彻阶段”,又经历了“刚体侵彻阶段”。当速度大于3.08 km/s 时,弹体已经被完全侵蚀,因此不包括刚体侵彻阶段。由于刚体侵彻阶段弹体仍然具有较高的速度,且侵彻的是受初始冲击波破坏的水泥砂浆靶体,因此刚体侵彻阶段对总侵彻的贡献较大。如果弹体完全侵蚀,失去刚体侵彻阶段,将导致总侵深的降低。因此,当撞击速度大于3.08 km/s 时,总侵彻深度随撞击速度的增大而显著降低。
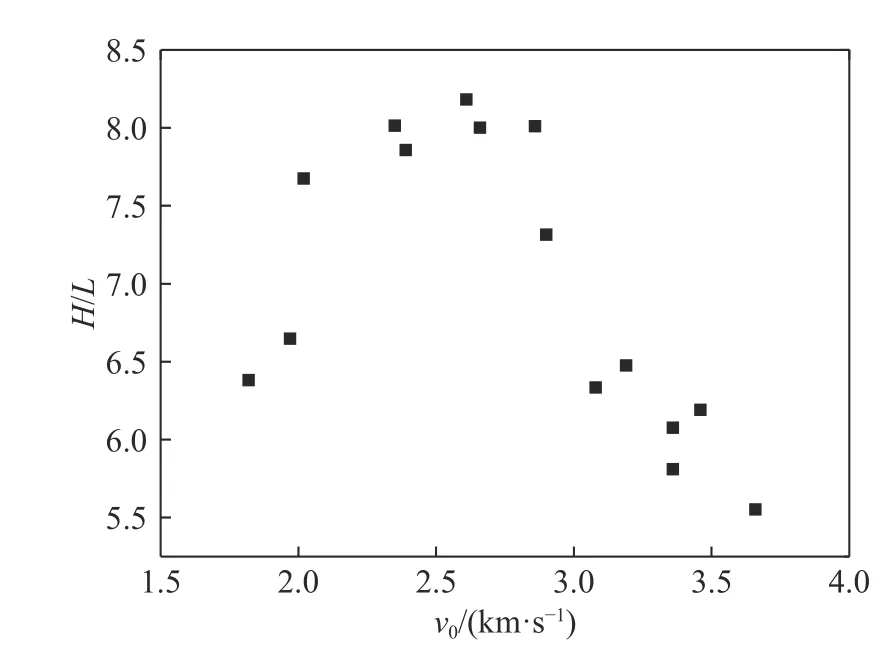
图 5 侵彻深度随撞击速度变化关系Fig. 5 Variation of penetration depth with impact velocity

图 6 不同撞击速度条件下的残余弹体Fig. 6 Residual projectiles at different impact velocities
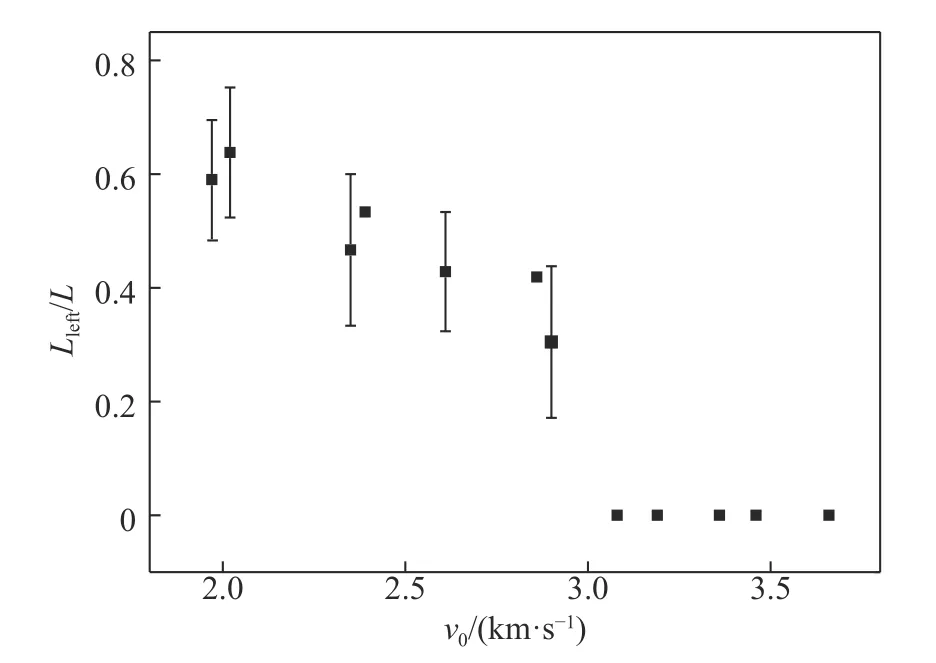
图 7 残余弹体长度随撞击速度变化规律Fig. 7 Variation of residual projectiles length with impact velocities
3 数值模拟方法校核
数值模拟方法有助于深入认识超高速撞击问题。影响数值模拟置信度的因素主要包括算法和物理模型。
在算法方面,目前针对超高速撞击过程中的大变形、高温高压的极端状态,发展了多种算法,采用较多的是SPH 方法和Euler 方法。由于SPH 方法可以通过颗粒间连接关系的失去自然的描述物理断裂,由于不稳定的问题,导致数值断裂,数值断裂经常和真正的物理断裂混淆在一起,影响结果的准确性,并导致计算终止。目前开展的超高速撞击的数值模拟工作中,Anderson 采用CTH 程序,Rosenberg 采用PISCES 程序和AUTODYN 程序的Euler 算法进行模拟,兰彬采用LS-DYNA 的ALE 方法进行模拟,以上超高速撞击数值模拟都采用了Euler 型有限元方法,说明研究者们更看重Euler 法在处理大变形问题时的计算精度和效率的优势。因此,本文中拟采用AUTODYN 软件的Euler 法进行数值模拟。
在材料模型方面,由于超高速撞击物理过程中,涉及弹靶材料从高温、高压、高应变率、大变形状态过渡到低温、低压、低应变率和小变形的过程,已有的材料模型大多针对某一特定物理过程,难以在全周期对超高速撞击过程进行精确描述,因此在物理模型方面存在一定的误差。另外,针对材料在本文弹靶组合和速度范围条件下的高温、高压、高应变率、大变形状态,缺乏相应的材料模型参数。最合适的办法应是根据超高速撞击的特点,建立能够描述整个撞击过程的材料模型(或是分段描述的材料模型),然后进行系统的材料静态、动态力学性能实验,获得准确的材料模型参数。但是这是非常复杂、困难的工作。因此,本文中首先从现有材料模型中优选出适合描述超高速撞击过程的材料模型,接下来利用基本的材料力学性能实验修正材料模型参数,然后利用该模型进行超高速撞击的数值模拟,最后用实验结果校核数值模拟,保证数值模拟结果在本文弹靶组合和速度范围内,能够较好地描述本文关心的侵彻深度和残余弹长问题。
弹体材料的本构模型方面,Steinberg 模型和Johnson-Cook 模型都是金属材料在高应变率下的常用本构模型,考虑到Johnson-Cook 本构关系在低压范围内模拟结果较好,而Steinberg 本构模型在高压范围内模拟结果较好。在应变率高于105s−1时,Steinberg 本构模型非常适用,因此,针对2~4 km/s 打击速度范围内的弹体材料本构关系,选用Steinberg 本构模型来描述。Steinberg 模型是美国劳伦斯-利弗莫尔国家实验室的Steinberg 等[10]于1980 年提出的能够描述物体高压、高温、高应变率条件下的本构模型,该模型不考虑应变率效应,只考虑温度效应和应变效应。因为在高应变率(105s−1)条件下,温度上升,材料强度变化不大,因此可以忽略应变率效应。
弹体材料的状态方程采用Grüneisen 状态方程,该状态方程能够较准确地描述材料在高压状态下的压力体积关系,即使当材料出现融化时计算结果也比较准确。
靶体材料的本构模型方面,常用的混凝土类材料的动态损伤本构模型包括HJC 模型[11]、RHT 模型[12]、TCK 模型、LLNL 模型、K&C 模型和BFK 模型等,其中HJC 模型和RHT 模型使用较为广泛。RHT 模型是基于HJC 模型发展而来的,该模型引入了三个强度极限面,包括失效面、弹性极限面和残余强度面,考虑了拉应力的破坏作用以及拉应力的应变率敏感性,因而该模型能够综合反映材料的压缩和拉伸损伤,继而更加完整地反映混凝土材料的动力学行为,近年来受到广泛关注。由于我们需要同时考虑压缩和拉伸损伤的材料模型,另外为采用AUTODYN 软件,需要尽量避免材料模型的二次开发。因此选用RHT模型作为水泥砂浆材料的本构模型,模型参数见表2。
为了更好地描述带孔隙的混凝土材料,靶体材料的状态方程选用压力-孔隙率(P-α)状态方程。
材料参数中静态强度、密度、模量采用静态实验值[13],其他采用AUTODYN 材料模型数据库中的值。
从侵彻深度、残余弹长两个方面对数值模拟方法进行校核。图8 为数值模拟得到的侵彻深度与实验结果的对比。数值模拟与实验结果在1.8~4 km/s 范围内趋势一致,均存在一个侵彻深度极大值,极大值对应的速度约为2.6 km/s。数值模拟得到的侵彻深度值与实验结果存在一定的差别,但是误差均不超过10%。图9 为数值模拟得到的残余弹长与实验结果的对比。随着速度的增加,数值模拟得到的残余弹长逐渐减小,当弹速达到3 km/s 时,弹体被完全侵蚀,这与实验中得到的残余弹长随弹速变化的规律基本吻合。从残余弹长数值来看,数值模拟得到的残余弹体直径相对于实验结果略小,但是数值模拟结果基本落在实验结果的误差棒内。
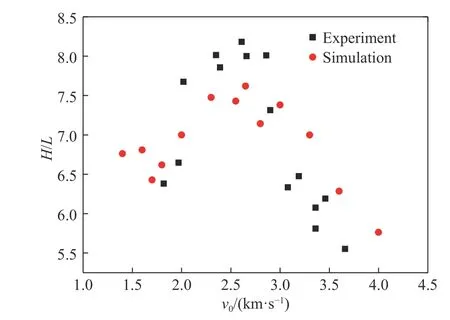
图 8 侵深随速度变化规律的数值模拟结果与实验结果的对比Fig. 8 Penetration depth as compared between experiments and numerical simulations
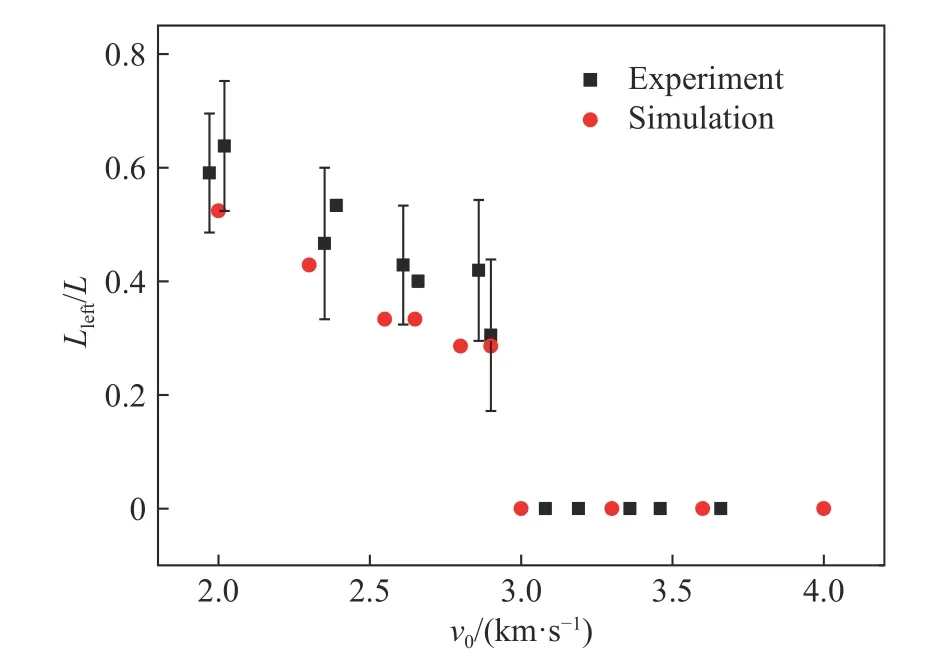
图 9 数值模拟得到的残余弹体长度与实验结果的对比Fig. 9 Residual projectile length as compared betweenexperiments and numerical simulations

表 2 水泥砂浆的材料模型参数Table 2 Material parameters of concrete
综上所述,本文中采用的数值模拟方法在侵彻深度和残余弹长这两个关键参量方面与实验结果吻合较好,说明该方法能够较好地描述超高速撞击物理过程,可在此基础上进行撞击机理探究。
4 讨 论
4.1 超高速撞击过程的阶段划分
图10 是数值模拟得到的3 km/s 的撞击速度下弹体尾部速度、弹靶界面速度、弹靶界面压力、侵彻深度随时间的变化关系。通过弹靶界面的压力随时间变化曲线,参照Eichelberger[14]提出的弹体超高速撞击的4 个阶段和Orphal[15]提出的第三侵彻阶段的概念,将超高速撞击过程分为4 个阶段:
(1)瞬态高压段,撞击开始的瞬间,弹体相对于靶体突然减速,于是产生一个强冲击波分别向靶板和弹体传播。由于弹体直径较小,弹体侧面稀疏波很快追赶并卸载初始的强冲击波,所以强冲击波脉宽很窄,作用时间约0~0.8 µs,压力最高达47 GPa。
(2)准定常侵彻阶段,卸载波经过几次反射后,形成一个准定常的流动条件,弹体和靶体连续破碎,驱动弹坑形成。该阶段弹靶界面的压力和速度都处于缓慢的下降状态,在19 µs 时,弹体尾部速度和侵蚀速度均下降至1 277 m/s,代表弹体停止侵蚀,之后将以刚体形式继续侵彻靶板。在此阶段,压力的持续时间取决于弹体中的卸载波与靶体内冲击波的作用时间,相同状态下,弹体的长度越长,准定常侵彻阶段持续的时间也越长。本文中选用的弹体长径比仅为3,所以准定常侵彻阶段持续时间较短,侵深也较小,仅占总侵深的约45%。
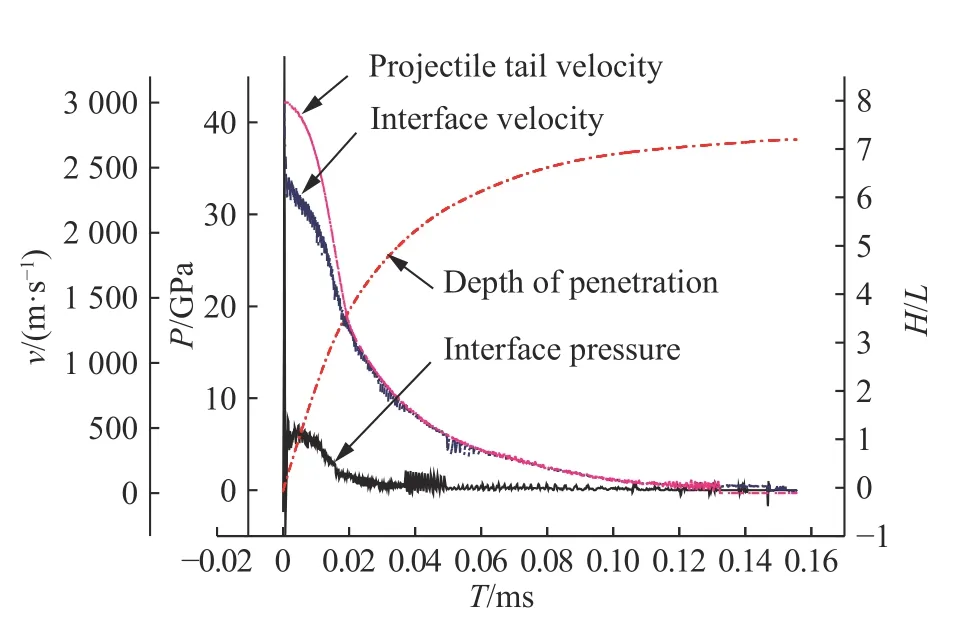
图 10 弹体尾部速度、界面速度、界面压力、侵彻深度随时间的变化关系( v0=3 km/s)Fig. 10 Time histories of projectile tail velocity,interface velocity, interface pressure and the penetration depth (v 0=3 km/s)
(3)第三侵彻阶段,该阶段弹体停止侵蚀,存在两种侵彻模式:一方面残余弹体以刚体的形式继续侵彻靶板,由于弹体密度高,靶体又经历了初始冲击破坏,所以当残余弹长较大时刚体侵彻的深度较大;另一方面铺在坑底的残余弹体碎屑和靶体材料仍然存在动能,弹坑在惯性作用下继续扩张,直到弹坑周围能量密度减小到不能克服材料变形阻力,弹坑就停止扩张。第三侵彻阶段包括刚性弹体的侵彻和靶板材料的惯性扩展开坑作用,机理复杂,又在总侵深中占较大比重(大约占总侵深的约55%),这给理论分析带来了很大挑战。
(4)回弹阶段:120 µs 之后,弹坑深度基本到达最大,靶板材料由于弹性恢复作用,产生与撞击方向相反的位移,但是位移量很小,可以忽略。
4.2 分阶段的侵彻深度
根据上节的分析,将成坑过程中不同阶段的侵彻深度数据和其他关键参数列于表3。重点关注准定常侵彻阶段和第三侵彻阶段的侵彻深度,瞬时开坑阶段和回弹阶段对侵彻深度的贡献很小,可以忽略不计。
从表3 和图11 可以看出,在撞击速度1.7~4 km/s 范围内,随着撞击速度增大,准定常侵彻阶段的侵彻深度随弹速增加呈缓慢增加的趋势,且侵彻深度与流体动力学极限差异不大,说明该阶段近似于流体侵彻。
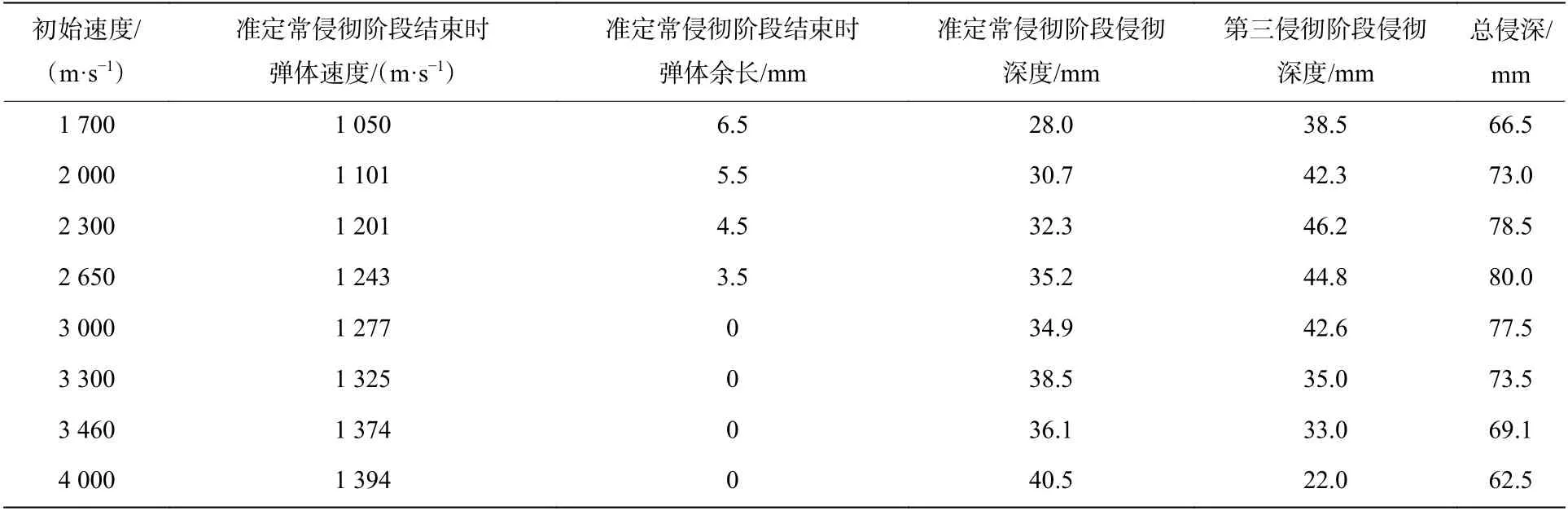
表 3 不同初始速度条件下的弹体速度、成坑深度和弹体长度的数值模拟结果Table 3 Simulated projectiles velocity, penetration depth and residual projectile length at different impact velocities
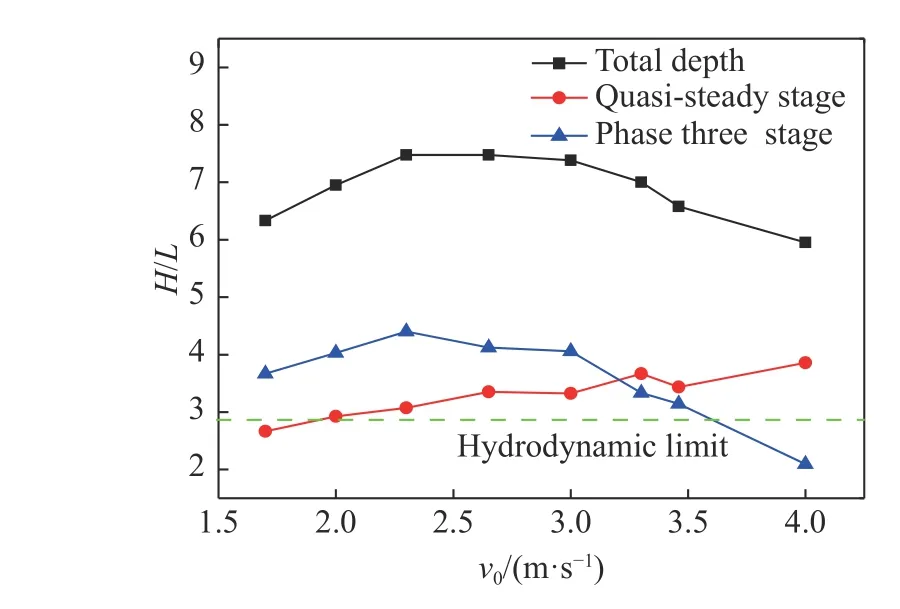
图 11 数值模拟得到的准定常侵彻阶段和第三侵彻阶段的侵彻深度和总侵彻深度的关系Fig. 11 Relationship of penetration depth between quasi-steady stage, phase three stage and the total penetration obtained by simulation
第三侵彻阶段的侵彻深度随弹速增大呈现先增大后减小的情况,在2.3 km/s 时达到极大值。当弹速在1 700~2 300 m/s 范围时,虽然弹体残余长度随弹速增加而减小,但是残余弹体的初始刚体侵彻速度(准定常侵彻阶段到第三侵彻阶段的转变速度)随撞击速度的增加而增加,所以弹体以刚体形式侵彻的能力仍然随撞击速度升高而缓慢升高。当弹速超过2 300 m/s 时,残余弹体长度快速降低,刚体侵彻能力也快速降低,仅能依靠坑底碎渣在残余速度的作用下对靶板的侵彻,导致第三侵彻阶段的侵彻深度逐渐降低。
通过图11 和表3 可以看出,准定常侵彻阶段的侵彻深度-撞击速度曲线缓慢递增,第三侵彻阶段的侵彻深度-撞击速度曲线先增大后减小,在2.3 km/s 时存在极大值。两者叠加之后得到的总侵深也呈现先增大后减小的趋势,侵彻深度极大值对应的速度小幅提升至2.6 km/s。王可慧[8]在结构弹体以1 500 m/s 以下的速度侵彻水泥砂浆靶的过程中发现随着撞击速度提高,弹体由刚体状态变为破碎状态,导致侵彻深度曲线出现拐点,由逐渐增加变为急剧下降,我们认为是刚体侵彻和半流体侵彻的分界点导致了侵彻深度拐点的出现。在超高速撞击条件下,拐点的产生机制与中低速不同,是由准定常侵彻阶段和第三侵彻阶段共同决定的,而不是由某一特定的分界点决定。因此,有理由认为钨合金弹体由低速到超高速侵彻混凝土靶的情况下,侵彻深度曲线可能出现两个拐点,一个是由于刚体侵彻和半流体侵彻的分界点而产生的,大约在1 000~1 400 m/s,另一个是由于准定常侵彻阶段和第三侵彻阶段的侵深变化导致的,大约在2 300~2 700 m/s。
残余弹长和残余弹体的初始刚体侵彻速度共同决定了刚体侵彻深度,而刚体侵彻深度在总侵深中占有较大比重。当弹体被完全侵蚀后,总侵深显著降低。因此,残余弹长对总侵深曲线中拐点的产生有一定影响,这与实验中发现的规律吻合。
准定常侵彻阶段的侵彻深度与流体动力学极限比较接近,用伯努利方程或修正的AT 模型可以描述。但在总侵深中,准定常侵彻阶段占比较小,如果需要建立总侵深的理论分析模型,还需重点分析残余弹体对受初始冲击破坏靶板的侵彻作用和坑底残渣在惯性作用下对靶板的开坑作用,难度较大,本文中暂不开展该部分工作。
5 结 论
为探究钨合金弹体超高速撞击混凝土靶的侵彻深度随撞击速度的变化规律,采用二级轻气炮开展了钨合金弹体以1.82~3.66 km/s 的速度撞击混凝土靶的实验,并利用AUTODYN 软件的Euler 算法对超高速撞击过程进行了数值模拟,得到的侵彻深度和残余弹长与实验结果吻合较好,可用于分析超高速撞击过程的具体图像和各物理量的变化过程。结合实验与数值模拟结果分析撞击过程,得到以下结论:
(1)超高速撞击条件下成坑是弹坑+弹洞型;
(2)侵深-速度曲线呈现先增大后减小的现象,在弹速2.6 km/s 附近存在侵彻深度极大值,约为8.5 倍弹长,而中低速侵彻得到的最大侵深也能达到约8 倍弹长,因此超高速撞击条件下的最大侵彻深度相对于中低速侵彻并没有明显优势。
(3)基于数值模拟得到的弹靶界面压力的时程曲线,将侵彻过程分为4 个阶段,其中准定常侵彻阶段和第三侵彻阶段是决定总侵深的主要阶段。
(4)随撞击速度增加,弹体侵蚀逐渐剧烈,此时准定常侵彻阶段的侵深变化不大,而第三侵彻阶段中的刚体侵彻部分大幅降低,导致总侵深大幅降低,使总侵深曲线呈现先增大后减小的现象。

